Codeforces Round #261 (Div. 2) E

Description

Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem.

You are given a weighted directed graph with n vertices and m edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path.

Help Pashmak, print the number of edges in the required path.

Input

The first line contains two integers n, m (2 ≤ n ≤ 3·105; 1 ≤ m ≤ min(n·(n - 1), 3·105)). Then, m lines follows. The i-th line contains three space separated integers: ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105) which indicates that there's a directed edge with weight wi from vertex ui to vertex vi.

It's guaranteed that the graph doesn't contain self-loops and multiple edges.

Output

Print a single integer — the answer to the problem.

Examples

input

3 3
1 2 1
2 3 1
3 1 1

output

1

input

3 3
1 2 1
2 3 2
3 1 3

output

3

input

6 7
1 2 1
3 2 5
2 4 2
2 5 2
2 6 9
5 4 3
4 3 4

output

6

Note

In the first sample the maximum trail can be any of this trails: .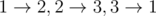

In the second sample the maximum trail is .

In the third sample the maximum trail is .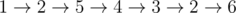

题意：按照权值递增循序走，能走出最长的路径是多少

解法：求出dp[u]=max(dp[u],dp[v]+1)(v起点，u终点）

根据权值从小到大排序，分别处理相同权值片段的长度，最后求最大值

#include<stdio.h>
//#include<bits/stdc++.h>
#include<string.h>
#include<iostream>
#include<math.h>
#include<sstream>
#include<set>
#include<queue>
#include<map>
#include<vector>
#include<algorithm>
#include<limits.h>
#define inf 0x7fffffff
#define INFL 0x7fffffffffffffff
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define LL long long
#define ULL unsigned long long
using namespace std;
const int M = 2000000;
int n,m;
struct P
{
    int v,u,w;
}H[M];
bool solve(P x,P y)
{
    return x.w<y.w;
}
int dp[M],ans[M];
int j;
int main()
{
    std::ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        cin>>H[i].v>>H[i].u>>H[i].w;
    }
    sort(H,H+m,solve);
    for(int i=0;i<m;i=j)
    {
        for(j=i;H[i].w==H[j].w&&j<m;j++)
        {
            ans[H[j].u]=dp[H[j].u];
        }
        for(j=i;H[i].w==H[j].w&&j<m;j++)
        {
            ans[H[j].u]=max(ans[H[j].u],dp[H[j].v]+1);
        }
        for(j=i;H[i].w==H[j].w&&j<m;j++)
        {
            dp[H[j].u]=ans[H[j].u];
        }
    }
    int Max=-1;
    for(int i=1;i<=n;i++)
    {
        Max=max(dp[i],Max);
    }
    cout<<Max<<endl;
    return 0;
}