84. 柱状图中最大的矩形
题目来源:力扣(LeetCode)https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
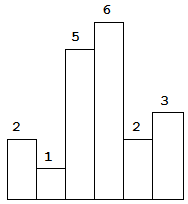
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
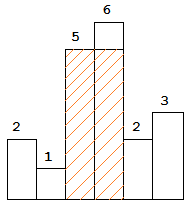
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
解题思路
思路:栈
在说栈之前,我们先说一下,关于暴力解,如何去解决这个问题。
题目中要我们去求能勾勒出最大矩形面积,其实求矩形面积,有两种方法:
- 固定宽度,高度变化,求最大面积
- 固定高度,改变宽度,求最大面积
在这道题当中,使用第二种方法是比较容易去求得结果。具体如何去实现?
这里,我们依次去遍历柱形的高度,然后对每个高度都向两边进行扩散,(当左右遇到柱形高度比当前柱形高度小的柱形时,那么将无法继续扩散)这样就能求出当前高度能扩散的最大宽度。当求出宽度时,就能够求出面积。依次去比较以每个柱形高度进行最大扩散的面积,最终确定最大的面积。
这里 Python 使用暴力解会超时,这里就不给出代码了 。(不过建议个人可尝试编写)
我们使用暴力解的时候,遍历的时候要从中间进行扩散,这里时间复杂度是 O(n^2),而空间复杂度为 O(1),因为只用了常数个变量。那么我们可以考虑使用【空间换时间】的思路,在我们进行遍历的时候去记录一些信息。
这里注意上面标注黑色字体加重的内容,【当左右遇到柱形高度比当前柱形高度小的柱形时,那么将无法继续扩散】,这里我们可以想到,问题的关键就是要找到左右两侧比当前柱形高度小的柱形,这样就能确定宽度。
这里我们构造一个单调栈。
单调栈:分为单调递增和递减的栈。
- 单调递增栈,栈内元素保持单调递增
- 单调递减栈,栈内元素保持单调递减
本题构建的栈是单调递增栈,具体如何操作:
- 如果遍历元素大于栈顶元素,则入栈
- 如果遍历的新元素较小时,就弹出栈内元素直至栈顶元素比新的元素小。
我们来看示例,[2,1,5,6,2,3]

我们构建栈,存储的是数组中的索引。
结合上面的图例来看,在这里,假设我们现在索引指向的元素是 6 时(这时,栈内的对应的是 1 5 6 的索引),下一个元素是 2,按照单调递增栈的操作,这里 6 需要出栈,那么 2 就是这个元素往后的第一个比它小的元素。当元素出栈之后,现在栈顶的元素就是出栈元素往前的第一个比其小的元素,即是此时的 5,这个时候,高度为 6 的这个柱形的宽度就能够确定下,进而面积也能够确定。
同理此时的栈顶索引对应的元素为 5,同样比 2 小,需要出栈,此时的栈顶对应元素为 1(跟上面的逻辑一样,这个就是出栈元素往前第一个比它小的元素),那么高度为 5 的宽度就能够确定下,即是元素 1 和元素 2 之间的宽度。
按照这个逻辑,具体的实现思路:
- 构建单调递增栈
- 遍历元素大于栈顶元素,入栈
- 如果遍历元素小于栈顶元素,进行出栈
- 出栈的同时,确定宽度,求出面积。
具体实现代码如下。
代码实现
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
size = len(heights)
# 这里我们使用哨兵节点,这样就能够避免非空判断
heights = [0] + heights + [0]
# 数组长度发生了变化
size += 2
# 将哨兵先放入栈中
stack = [0]
ans = 0
for i in range(1, size):
# 与栈顶元素比较,进行判断是否要入栈
# 出栈的逻辑
while heights[i] < heights[stack[-1]]:
cur_height = heights[stack.pop()]
# 确定宽度
cur_width = i - stack[-1] - 1
ans = max(ans, cur_height * cur_width)
stack.append(i)
return ans
实现结果
总结
- 先使用暴力解,发现解决此问题的方法,可以先固定高度,求宽度,进而求面积;
- 构建单调递增栈,实现一次遍历求得结果
- 首先,栈的实现操作,遍历元素大于栈顶元素时,进行入栈。
- 当遍历元素小于栈顶元素时,要进行出栈,这个时候确定宽度,求得面积。
- 代码中使用了哨兵节点,这里主要是为了避免非空判断,可以让代码更简洁。
欢迎关注微信公众号《书所集录》