推了半天约数的关系无果,果断转向等差数列+求根公式。
公式1:
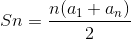
化n得:

配成二元一次方程形式:

再转化为代码解方程就可以了~

#include<bits/stdc++.h> using namespace std; double m,t,x1,x2; int main() { cin>>m; for(double i=2;i<m;i++) { x1=(-1+sqrt(1-4*(i-i*i-2*m)))/2; if(x1>i&&x1==floor(x1))cout<<i<<' '<<x1<<endl; } return 0; }
公式2:
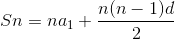
配成二元一次方程形式
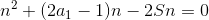

#include<bits/stdc++.h> using namespace std; double m,t,x1,x2; int main() { cin>>m; for(double i=2;i<m;i++) { x1=((2*i-1)+sqrt((2*i-1)*(2*i-1)+8*m))/2; if(x1>i&&x1==floor(x1))cout<<i<<' '<<x1-i<<endl; } return 0; }
上面两个公式转换为代码:开一个2~m-1的循环(1和m没有用,易证),a1是循环当前位置i的值,是常量,公式1的an和公式2的n都是要求的未知数,其余都是常量。
两个公式的区别:
- 公式1可以直接求出来整个数列的最后一项,直接输出就好。
- 公式2求出来的是整个数列第一项+最后一项的值,最后还要减去数列第一项。
注意事项:
- 两个公式都弄出来x1和x2,较小的x1直接省略,不用写到程序里,因为它小于0。
- 只有x2为整数才可以哦。判定方法:
x2==floor(x2)
3.要开double(废话
