6树？

树的定义

树的定义

树（Tree）是 n （n>=0）个结点的有限集。 n=0 时称为空树。在任意一颗非空树中，

（1）有且仅有一个特定的称为根结点（Root）；

（2）当 n>1 时，其余结点可分为 m（m>0）个互不相交的有限集 T₁、T₂……、T_m，其中每一个集本身又是一棵树，并且称为根的子树（SubTree）。

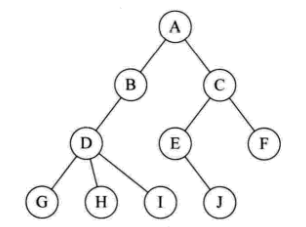
树的定义其实就是递归的方法。

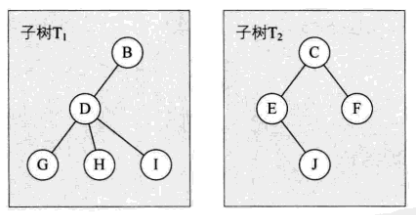
如上图的子树 T₁ 和子树 T₂ 就是根节点 A 的子树。当然，D、G、H、I 组成的树又是 B 为结点的子树，E、J 组成的树是 C 为结点的子树。

强调：

n>0 时根结点时唯一的，不可能存在多个根节点，别和现实中的大树混在一起，现实中的树有很多根须，那是真实的树，数据结构中的树只能有一个根节点。

m>0 时，子树的个数没有限制，但它们一定是互不相交的。如下图的两个结构就不符合树的定义，因为它们都有相交的子树。

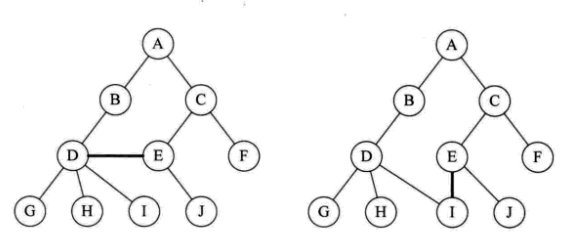
结点分类

树的节点包含一个数据元素及若干指向其子树的分支。

结点拥有的子树数称为结点的度（Degree）。度为 0 的结点称为叶结点（Leaf）或终端结点；度不为 0 的结点称为非终端结点或分支节点。除根结点之外，分支结点也称为内部节点。树的度是树内各结点的度的最大值。如图：

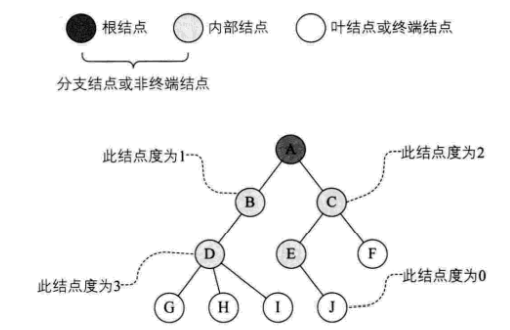
 这棵树结点的度的最大值是结点 D 的度，为 3，所以树的度也为 3。

结点间的关系

• 结点的子树的根称为该结点的孩子（Child），相应地，该结点称为孩子的双亲（Parent）。
• 同一个双亲的孩子之间互称兄弟（Sibling）。
• 结点的祖先是从根到该结点所经分支上的所有结点。如：对于 H 来说，D、B、A 都是它的祖先。
• 以某结点为根的子树中的任一结点都成为该结点的子孙。如：B 的子孙有D、G、H、I，如图：

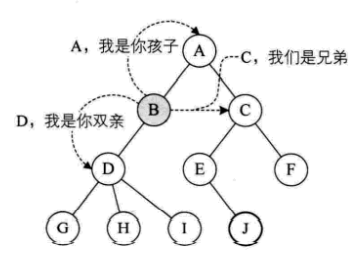
树的其他相关概念

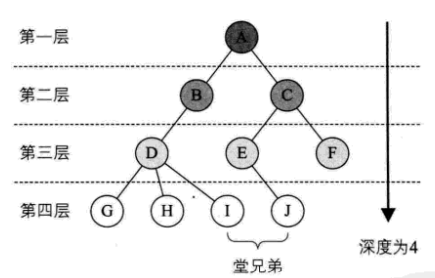
• 结点的层次（Level）从根开始定义起，根为第一层，根的孩子为第二层。即：某结点在第 i 层，则其子树的根就在第 i 层。
• 双亲在同一层的互为堂兄弟。如：D、E、F 为堂兄弟， G、H、I、J 也是。
• 树中结点的最大层次称为树的深度（Depth）或高度。

如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。

森林（Forest）是 m（m>=0）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。如 B 和 C 两棵子树其实就可以理解为森林。

线性结构和树结构区别

线性结构：

• 第一个数据元素：无前驱
• 最后一个数据元素：无后继
• 中间元素：一个前驱一个后继

树结构：

• 根结点：无双亲，唯一
• 叶结点：无孩子，可以多个
• 中间结点：一个双亲多个孩子

树的抽象数据类型

树的存储结构

树的表示法：双亲表示法、孩子表示法、孩子兄弟表示法

双亲表示法

除了根节点外，其余每个结点，它不一定有孩子，但是一定有且仅有一个双亲。

同时在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。即：每个结点除了知道自己是谁以外，还知道它的双亲在哪。如图：

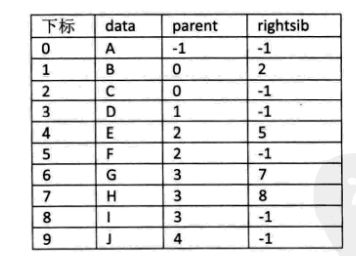
其中 data 是数据域，存储数据信息；parent 是指针域，存储该结点的双亲在数组中的下标。

双亲表示法的结点结构定义代码如下：

根节点没有双亲，约定根结点的位置域设为 -1。如图：

 

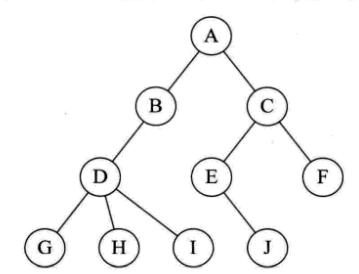
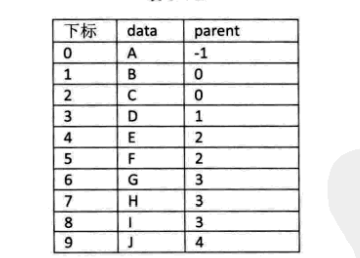
这样的存储结构，可以根据结点的 parent 指针很容易找到它的双亲结点，所用时间复杂度为 O(1)，直到 parent 为 -1 时，表示找到树的根节点。

但是，如果想要知道结点的孩子是什么，则需要遍历整个结构才行。

改进：

增加结点最左边的孩子的域，暂称为长子域，没有孩子的结点，长子域设为 -1，如图：

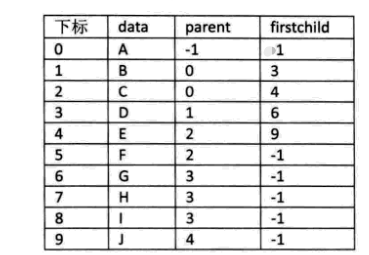
对于有 0 个或者 1 个孩子结点来说，这样的结构解决了要找结点孩子的问题。

原书写道：甚至是有 2 个孩子，知道了长子是谁，另一个当然就是次子了。（暂时没明白，知道长子是谁，怎么知道次子，难道不用遍历就能得到吗？没想出来怎么靠这个结构不遍历就能得到次子，有大神指教下吗？）

各兄弟之间的关系，双亲是无法体现的，则需要增加一个右兄弟域来体现，即：每一个结点如果它存在右兄弟，则记录有兄弟的下标，不存在，则设为 -1。如图：