多类逻辑回归
from mxnet import gluon
from mxnet import ndarray as nd
def SGD(params, lr):
for param in params:
param[:] = param - lr * param.grad
def transform(data, label):
return data.astype('float32')/255, label.astype('float32')
mnist_train = gluon.data.vision.FashionMNIST(train=True, transform=transform)
mnist_test = gluon.data.vision.FashionMNIST(train=False, transform=transform)
# 标签对应的服饰名字
def get_text_labels(label):
text_labels = [
't-shirt', 'trouser', 'pullover', 'dress,', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot'
]
return [text_labels[int(i)] for i in label]
# 数据读取
batch_size = 256
# gluon.data的DataLoader 函数,它每次 yield ⼀个批量
train_data = gluon.data.DataLoader(mnist_train, batch_size, shuffle=True)
test_data = gluon.data.DataLoader(mnist_test, batch_size, shuffle=False)
#初始化参数
num_inputs = 784
num_outputs = 10
W = nd.random_normal(shape=(num_inputs, num_outputs))
b = nd.random_normal(shape=num_outputs)
params = [W, b]
for param in params:
param.attach_grad()
# 定义模型
# 多分类中,输出为每个类别的概率,这些概率和为1,通过softmax函数实现
from mxnet import nd
def softmax(X):
exp = nd.exp(X)
partition = exp.sum(axis=1, keepdims=True)
return exp / partition
def net(X):
return softmax(nd.dot(X.reshape((-1, num_inputs)), W) + b)
# 交叉熵损失函数
# 我们需要定义⼀个针对预测为概率值的损失函数。其中最常⻅的是交叉熵损失函数,它将两个概率
# 分布的负交叉熵作为⽬标值,最小化这个值等价于最⼤化这两个概率的相似度。
def corss_entropy(yhat, y):
return - nd.pick(nd.log(yhat), y)
# 计算精度
# 给定⼀个概率输出,我们将预测概率最⾼的那个类作为预测的类,然后通过⽐较真实标号得到是否预测正确
def accuracy(output, label):
return nd.mean(output.argmax(axis=1)==label).asscalar()
def evaluate_accuracy(data_iterator, net):
acc = 0
for data, label in data_iterator:
output = net(data)
# acc_tmp = accuracy(output, label)
acc = acc + accuracy(output, label)
return acc/len(data_iterator)
# print(evaluate_accuracy(test_data, net))
#
# import sys
# sys.path.append('..')
from mxnet import autograd
learning_rate = 0.1
epochs = 5
for epoch in range(epochs):
train_loss = 0
train_acc = 0
for data, label in train_data:
with autograd.record():
output = net(data)
loss = corss_entropy(output, label)
loss.backward()
# 将梯度做平均,这样学习率会对 batch size 不那么敏感
SGD(params, learning_rate / batch_size)
train_loss = train_loss + nd.mean(loss).asscalar()
train_acc += accuracy(output, label)
# 模型训练完之后进行测试
test_acc = evaluate_accuracy(test_data, net)
print("Epoch %d. Loss: %f, Train acc %f, Test acc %f" % (
epoch, train_loss / len(train_data), train_acc / len(train_data), test_acc))
# 对新的样本进行标签预测
# 训练完之后,W,b参数已经固定,输入data,得到label就是预测过程
data, label = mnist_test[0:9]
print('true labels')
print(get_text_labels(label))
predicted_labels = net(data).argmax(axis=1)
print('predicted labels')
print(get_text_labels(predicted_labels.asnumpy()))
多类逻辑回归 — 使用Gluon
from mxnet import gluon
from mxnet import ndarray as nd
from mxnet import autograd
def transform(data, label):
return data.astype('float32') / 255, label.astype('float32')
mnist_train = gluon.data.vision.FashionMNIST(train=True, transform=transform)
mnist_test = gluon.data.vision.FashionMNIST(train=False, transform=transform)
batch_size = 256
train_data = gluon.data.DataLoader(mnist_train, batch_size, shuffle=True)
test_data = gluon.data.DataLoader(mnist_test, batch_size, shuffle=False)
num_inputs = 784
net = gluon.nn.Sequential()#定义空模型
with net.name_scope():
net.add(gluon.nn.Flatten()) # 将数据展开为batch_size*X格式的
net.add(gluon.nn.Dense(10))#输出为10
net.initialize()#初始化
softmax_cross_entropy = gluon.loss.SoftmaxCrossEntropyLoss() # Softmax 与CrossEntropyLoss的复合函数
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.1})#优化
def accuracy(output, label):
return nd.mean(output.argmax(axis=1) == label).asscalar()
def evaluate_accuracy(test_data, net):
acc = .0
for data, label in test_data:
output = net(data)
acc += accuracy(output, label)
return acc / len(test_data)
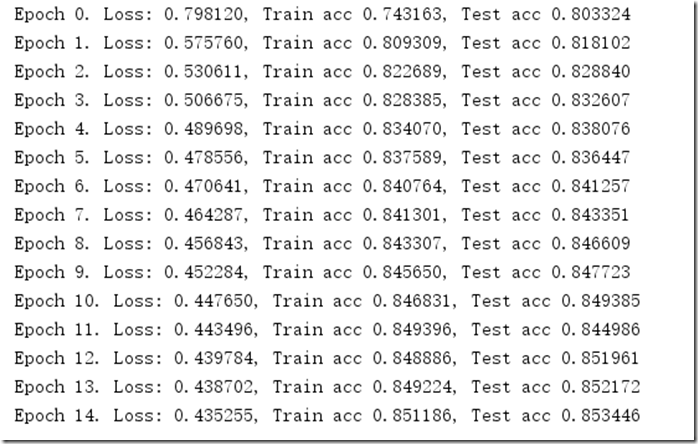
epochs = 15
for epoch in range(epochs):
total_loss = .0
total_acc = .0
for data, label in train_data:
with autograd.record():
output = net(data)
loss = softmax_cross_entropy(output, label)
loss.backward()
trainer.step(batch_size)#更新模型
total_loss += nd.mean(loss).asscalar()
total_acc += accuracy(output, label)
test_acc = evaluate_accuracy(train_data, net)
print("Epoch %d. Loss: %f, Train acc %f, Test acc %f" % (
epoch, total_loss / len(train_data), total_acc / len(train_data), test_acc))