【ML-13-3】隐马尔科夫模型HMM--Baum-Welch(鲍姆-韦尔奇)
【ML-13-4】隐马尔科夫模型HMM--预测问题Viterbi(维特比)算法
目录
- 引言
- 直接计算
- 前向算法
- 前向算法实例
- 后向算法
- HMM常用概率的计算
一、引言
在【ML-13-1】隐马尔科夫模型HMM中,我们讲到了HMM模型的基础知识和HMM的三个基本问题,本篇我们就关注于HMM第一个基本问题的解决方法。即给定模型λ=(A,B,π)和观测序列Q={q1,q2,...,qT},计算模型 λ 下观测到序列Q出现的概率P(Q|λ)
前向概率-后向概率指的其实是在一个观测序列中,时刻t对应的状态为si的概率值转换过来的信息。
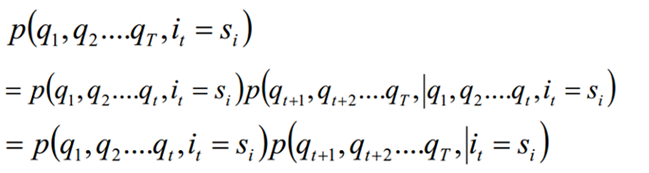
下图中(隐含用q表示,观测用y表示),前者为前向概率(所有的1-t的观测状态和t时刻的隐含状态),后者为后向概率

二、直接计算
按照概率公式,列举所有可能的长度为T的状态序列I={i1,i2,...,iT},求各个状态序列I与观测序列Q={q1,q2,...,qT}的联合概率P(Q,I;λ),然后对所有可能的状态序列求和,从而得到最终的概率P(Q;λ)
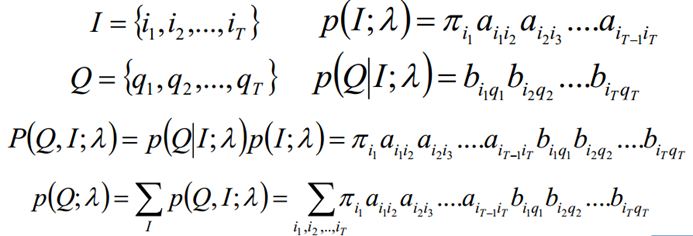

前向后向算法就是来帮助我们在较低的时间复杂度情况下求解这个问题的。
三、前向算法
前向后向算法是前向算法和后向算法的统称,这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。
前向算法本质上属于动态规划的算法,也就是我们要通过找到局部状态递推的公式,这样一步步的从子问题的最优解拓展到整个问题的最优解。
定义:给定λ,定义到时刻t部分观测序列为q1,q2,...,qt且隐含状态为si的概率为前向概率。记做:
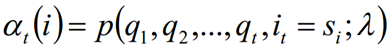
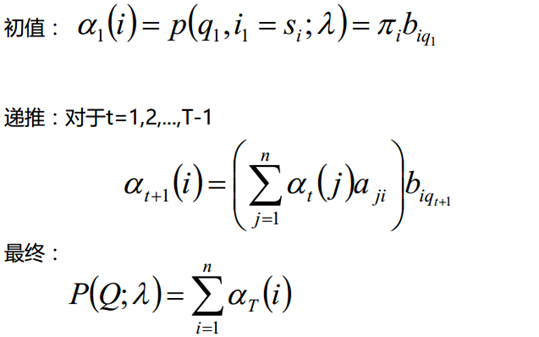
其中推导过程如下,也可以自己进行理解:在t+1时刻的i状态,可能是由每一个状态经过变换而来

从递推公式可以看出,我们的算法时间复杂度是O(TN^2),比暴力解法的时间复杂度O(TN^T)少了几个数量级。
四、前向算法实例
4.1 例题
假设有三个盒子,编号为1,2,3;每个盒子都装有黑白两种颜色的小球,球的比例如下:
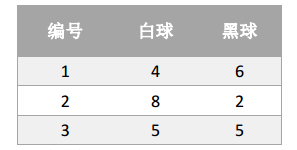
按照下列规则的方式进行有放回的抽取小球,得到球颜色的观测序列:
- 按照π的概率选择一个盒子,从盒子中随机抽取出一个小球,记录颜色后,放回盒子中;
- 按照某种条件概率选择新的盒子,重复该操作;
- 最终得到观测序列:"白黑白白黑
- 状态集合:S={盒子1,盒子2,盒子3}
- 观测集合:O={白,黑}
- 状态序列和观测序列的长度T=5
- 初始概率分布π
- 状态转移概率矩阵A
- 观测概率矩阵B
在给定参数π、A、B的时候,得到观测序列为"白黑白白黑"的概率是多少??注意在这个过程中,观察者只能看到球的颜色序列,却不能看到球是从哪个盒子里取出的。

4.2 计算过程


得到最终的结果:

五、后向算法
熟悉了用前向算法求HMM观测序列的概率,现在看看怎么用后向算法求HMM观测序列的概率。
后向算法和前向算法非常类似,都是用的动态规划,唯一的区别是选择的局部状态不同,后向算法用的是"后向概率",那么后向概率是如何定义的呢?
定义:给定λ,定义到时刻t状态为si的前提下,从t+1到T部分观测序列为qt+1,qt+2,...,qT的概率为后向概率。记做:
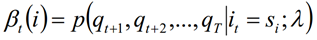
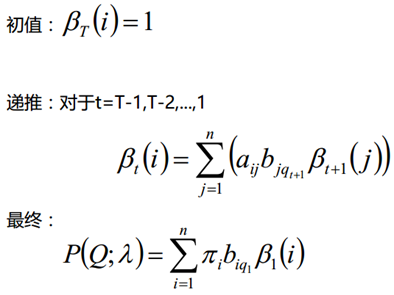
推导:

根据这个式子,同样可以算出上节中的概率,求得得结果一样得,本文不再举例。
六、HMM常用概率的计算
利用前向概率和后向概率,我们可以计算出HMM中单个状态和两个状态的概率公式。
6.1 单个状态的概率
求给定模型λ和观测序列Q的情况下,在时刻t处于状态si的概率,记做:
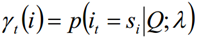
单个状态概率的意义主要是用于判断在每个时刻最可能存在的状态,从而可以得到一个状态序列作为最终的预测结果。
利用前向概率和后向概率的定义可知:
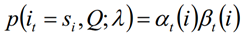
由上面两个表达式可知:
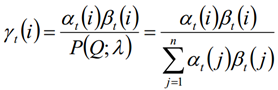
6.2 两个状态的联合概率
求给定模型λ和观测序列Q的情况下,在时刻t处于状态si并时刻t+1处于状态sj概率,记做:

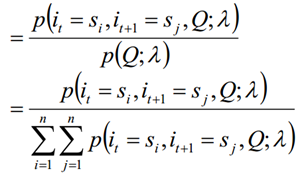
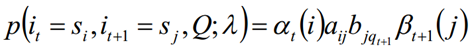
6.3 上述两种求和可以得到:
附件一:前向概率
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
# --encoding:utf-8 -- """课堂上实现的一个计算HMM模型中前向概率的一个算法实现(前向算法)""" import numpy as np def calc_alpha(pi, A, B, Q, alpha): """ 计算前向概率alpha,并将结果保存到alpha矩阵中(T*n) :param pi: 1*n :param A: n*n :param B: n*m :param Q: 1*T => T的数组 :param alpha: T*n :return: alpha """ # 1. 获取相关的变量信息 n = np.shape(A)[0] T = np.shape(Q)[0] # 2 更新t=1时刻的前向概率值 for i in range(n): alpha[0][i] = pi[i] * B[i][Q[0]] # 3. 更新t=2... T时刻对应的前向概率值 tmp = np.zeros(n) for t in range(1, T): # 迭代计算t时刻对应的前向概率值 for i in range(n): # 计算时刻t状态为i的前向概率 # a. 计算上一个时刻t-1累计到当前状态i的概率值 for j in range(n): tmp[j] = alpha[t - 1][j] * A[j][i] # b. 更新时刻t对应状态i的前向概率值 alpha[t][i] = np.sum(tmp) * B[i][Q[t]] # 4. 返回结果 return alpha if __name__ == '__main__': # 测试 pi = np.array([0.2, 0.5, 0.3]) A = np.array([ [0.5, 0.4, 0.1], [0.2, 0.2, 0.6], [0.2, 0.5, 0.3] ]) B = np.array([ [0.4, 0.6], [0.8, 0.2], [0.5, 0.5] ]) # 白,黑,白,白,黑 Q = [0, 1, 0, 0, 1] alpha = np.zeros((len(Q), len(A))) # 开始计算 calc_alpha(pi, A, B, Q, alpha) # 输出最终结果 print(alpha) # 计算最终概率值: p = 0 for i in alpha[-1]: p += i print(Q, end="->出现的概率为:") print(p) |
结果:
[[0.08 0.4 0.15 ]
[0.09 0.0374 0.1465 ]
[0.032712 0.093384 0.037695 ]
[0.01702872 0.04048728 0.03530505]
[0.0142037 0.00651229 0.01829338]]
[0, 1, 0, 0, 1]->出现的概率为:0.03900936690000001
附件一:手写练习



