目录
- 向量对向量
- 标量对多个向量
- 标量对多个矩阵
- 矩阵向量求导小结
求导的自变量和因变量直接有复杂的多层链式求导的关系,此时微分法使用起来也有些麻烦。需要一些简洁的方法。
本文我们讨论矩阵向量求导链式法则,使用该法则很多时候可以帮我们快速求出导数结果。如果遇到其他资料求
导结果不同,请先确认布局是否一样。
若没有特殊说明,默认情况定义如下:求导的自变量用x表示标量,x表示n维向量,X表示m×n维度的矩阵,求导的因变量用y表示标量,y表示m维向量,Y表示p×q维度的矩阵。默认向量为列向量,若是行向量,本文全部使用对应字母的转置表示。
总的求导准则:形式和平时高中所述的链式求导方式一样,这里矩阵和向量求导一定要注意维度统一。
一、向量对向量
假设多个向量存在依赖关系,比如三个向量 x → y → z 存在依赖关系,则我们有下面的链式求导法则:

维度探讨:假设x y z 的维度分别为m,n,p,∂z/∂x 是 p×m,∂z/∂y 是 p×n,∂y/∂x 是 n×m,符合矩阵乘法维度原则。
二、标量对多个向量
2.1 3个向量
最后到1标量的依赖关系: x → y → z ,此时很容易发现维度不相容。不能再简单套用上面的式子,而做了对应的变形:

维度探讨:假设x y z 的维度分别为m,n,1,∂z/∂x 是 m×1,(∂y/∂x)T 是 m×n,∂z/∂x 是 n×1,符合矩阵乘法维度原则。
2.2 多个向量
对于更加复杂的形式:如: y1 → y2 →…… yn → z ,则表达式为:
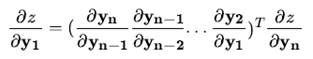
2.3 实际应用
ML-2最小二乘法中使用到的,最小二乘法优化的目标是最小化如下损失函数:

对上述进行如下假设:
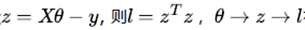
很容易得到以下表达式:
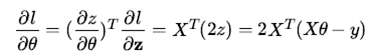
三、标量对多个矩阵
假设: X → Y → z 存在依赖关系,则我们有下面的链式求导法则:
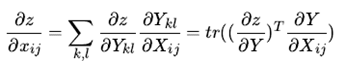
上面的式子是矩阵迹性质来的,不是特别实用,也不便于推广。我们再看一个偏难得问题:
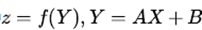
同样还是如此,

我们再来看看后半部分的导数:


那么最终的标签链式求导公式转化为:
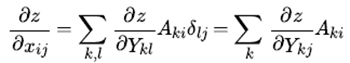
排列成矩阵即为:

对上面的式子做个总结:

维度探讨:假设Y A X 的维度分别为p×n,p×m,m×n,∂z/∂X是m×n,(A)T 是 m×p,∂z/∂Y是 p×n,符合矩阵乘法维度原则。
这结论在是一个向量x的时候也成立,即

同理:如果要求导的自变量在左边,线性变换在右边,也有类似稍有不同的结论如下:
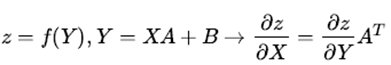

使用好上述四个结论,对于机器学习尤其是深度学习里的求导问题可以非常快的解决
四、矩阵向量求导小结
矩阵向量求导的三种方法:定义法,微分法和链式求导法。在同等情况下,优先考虑链式求导法,尤其是第三节的四个结论。其次选择微分法、在没有好的求导方法的时候使用定义法是最后的保底方案。
基本上大家看了系列里这四篇后对矩阵向量求导就已经很熟悉了,对于机器学习中出现的矩阵向量求导问题已足够。
主要来自: https://www.cnblogs.com/pinard/p/10825264.html
附件:手写推导
