目录
- 矩阵向量求导之定义法
- 矩阵向量求导之微分法
若没有特殊说明,默认情况定义如下:求导的自变量用x表示标量,x表示n维向量,X表示m×n维度的矩阵,求导的因变量用y表示标量,y表示m维向量,Y表示p×q维度的矩阵。默认向量为列向量,若是行向量,本文全部使用对应字母的转置表示。
一、矩阵向量求导之定义法
1.1 标量对向量求导的一些基本法则
1) 常量对向量的求导结果为0。
2)线性法则:如果都是实值函数 f,g, 为常数c1,c2,则:
![]()
3) 乘法法则:如果都是实值函数f,g,则:
![]()
要注意的是如果不是实值函数,则不能这么使用乘法法则。
4) 除法法则:如果f,g都是实值函数,且g(x)≠0,则
![]()
1.2 用定义法求标量对向量求导
由于所谓标量对向量的求导,其实就是标量对向量里的每个分量分别求导,最后把求导的结果排列在一起,按一个向量表示而已。那么我们可以将实值函数对向量的每一个分量来求导,最后找到规律,得到求导的结果向量。
首先我们来看一个简单的例子:
![]()
根据定义,我们先对的第i个分量进行求导,这是一个标量对标量的求导,如下:
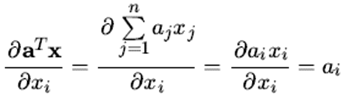
可见,对向量的第i个分量的求导结果就等于向量的第i个分量。由于我们是分母布局,最后所有求导结果的分量组成
的是一个n维向量。那么其实就是向量。也就是说:
![]()
同样的思路,我们也可以直接得到:
![]()
给一个简单的测试,大家看看自己能不能按定义法推导出:
![]()
再来看一个复杂一点点的例子:
![]()
我们对x的第k个分量进行求导如下:

这个第k个分量的求导结果稍微复杂些了,仔细观察一下,第一部分是矩阵A的第k列转置后和x相乘得到,第二部分
是矩阵的第k行和x相乘得到,排列好就是:
![]()
从上面可以看出,定义法求导对于简单的实值函数是很容易的,但是复杂的实值函数就算求出了任意一个分量的导
数,要排列出最终的求导结果还挺麻烦的,因此我们需要找到其他的简便一些的方法来整体求导,而不是每次都先去针对任意一个分量,再进行排列。
1.3 定义法求解标量对矩阵求导
其实思路和标量对向量的求导是类似的,只是最后的结果是一个和自变量同型的矩阵。
我们还是以一个例子来说明。
![]()
其中, a是m维向量, b是n维向量, X是 m × n 的矩阵。
我们对矩阵 X 的任意一个位置的 Xij求导,如下:
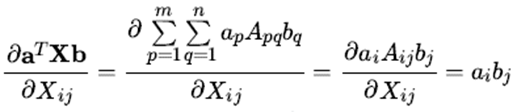
即求导结果在( i , j )位置的求导结果是a向量第i个分量和b第j个分量的乘积,将所有的位置的求导结果排列成一个m × n 的矩阵,即为abT,这样最后的求导结果为:
![]()
1.4 用定义法求解向量对向量求导
先来一个简单的例子:
![]()
其中A是 n × m 的矩阵。x,y分别为m,n维向量。需要求导∂Ax/∂x,根据定义,结果应该是一个m × n的矩阵
先求矩阵的第i行和向量的内积对向量的第j分量求导,用定义法求解过程如下:
![]()
可见矩阵 A的第i行和向量的内积对向量的第j分量求导的结果就是矩阵 A的位置的( i , j )值。排列起来就是一个矩阵
了,由于我们分子布局,所以排列出的结果是A,而不是A的转置
二、矩阵向量求导之微分法
使用定义法虽然已经求出一些简单的向量矩阵求导的结果,但是对于复杂的求导式子,则中间运算会很复杂,同时求
导出的结果排列也是很头痛的。故推出微分法。
2.1 矩阵微分的性质

2.2 矩阵微分
多变量的情况,则微分可以写成:
![]()
从上次我们可以发现标量对向量的求导和它的向量微分有一个转置的关系。现在我们再推广到矩阵。矩阵微分定义为:
![]()
其中第二步使用了矩阵迹的性质,即迹函数等于主对角线的和。即
![]()
从上面矩阵微分的式子,我们可以看到矩阵微分和它的导数也有一个转置的关系,不过在外面套了一个迹函数而已。
由于标量的迹函数就是它本身,那么矩阵微分和向量微分可以统一表示,即:
![]()
2.3 用微分法求标量对矩阵
我们先看第一个例子,我们使用定义法中的一个求导问题:
![]()
首先,我们使用2.1微分乘法的性质对求微分,得到:
![]()
第二步,就是两边套上迹函数,即:
![]()
其中第一到第二步使用了上面迹函数性质1,第三步到第四步用到了上面迹函数的性质3.
根据我们矩阵导数和微分的定义,迹函数里面在dX左边的部分baT,加上一个转置即为我们要求的导数,即:
![]()
以上就是微分法的基本流程,先求微分再做迹函数变换,最后得到求导结果。比起定义法,我们现在不需要去对矩阵
中的单个标量进行求导了。 再来看看:
![]()
![]()
其中第三步到第4步使用了上面迹函数的性质5. 这样我们的求导结果为:
![]()
2.4 迹函数对向量矩阵求导
由于微分法使用了迹函数的技巧,那么迹函数对对向量矩阵求导这一大类问题,使用微分法是最简单直接的。下面给
出一些常见的迹函数的求导过程,也顺便给大家熟练掌握微分法的技巧。
![]()
这个直接根据2.2 矩阵微分的定义即可得到。 再来看看:
![]()
![]()
因此可以得到:
![]()
最后来个更加复杂的迹函数求导:

![]()
因此可以得到:
![]()
2.5 小结
使用矩阵微分,可以在不对向量或矩阵中的某一元素单独求导再拼接,因此会比较方便,当然熟练使用的前提是对上
面矩阵微分的性质,以及迹函数的性质熟练运用。
还有一些场景,求导的自变量和因变量直接有复杂的多层链式求导的关系,此时微分法使用起来也有些麻烦。如果我
们可以利用一些常用的简单求导结果,再使用链式求导法则,则会非常的方便。
主要来自:
https://www.cnblogs.com/pinard/p/10791506.html
https://www.cnblogs.com/pinard/p/10773942.html
附件:手写推导
