目录
- 复数形态
- 傅里叶变换
- 傅里叶变换的意义
一、复数形态
1.1 直角坐表示
高中所学:复数可以在复平面(complex plane)上表示,复平面横纵坐标分别为实部和虚部,下图就是复数 4+3i 在复平面上的表示。
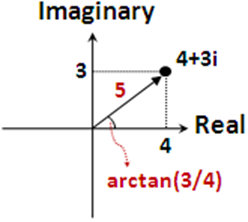
1.2 极坐标表示
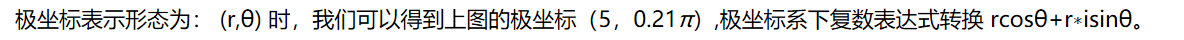
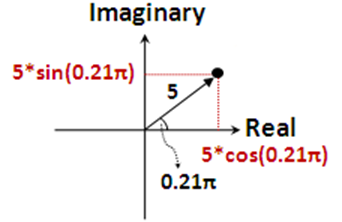
1.3 指数表示
著名的欧拉公式:
![]()
当 r=1,θ=π 时,可以得到数学届代表性公式:
![]()
其实欧拉公式可以从波形取直观理解:

可以看出,当俯视复数波时,观察到的投影即是一个实数波,即cosθ;当从左侧测视时,得到的投影即是虚部:sinθ。
当然上面的式子还有一个更为普遍的公式:
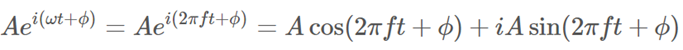
其中,A为振幅,ω为角速度,f为频率,ϕ为初试相位,这部分系数和高中课本三角函数所述相同。
另外:欧拉公式的另一种解释-使用泰勒公式:
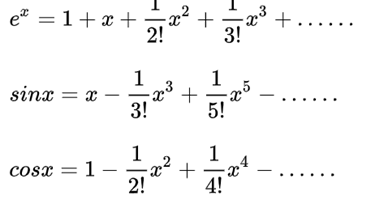
把x替换成it,就可以得出

二、傅里叶变换公式
傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个"傅里叶级数"或"傅里叶变换"。如今的计算机深度学习也会用到这些,如Gabor滤波器等。本文作简单介绍:
傅里叶他老人家生于1768年,死于1830年。故傅里叶变化技术也算是老树开新花。
2.1 傅里叶级数的公式
(推导见下文的附件一,感兴趣的可以浏览)
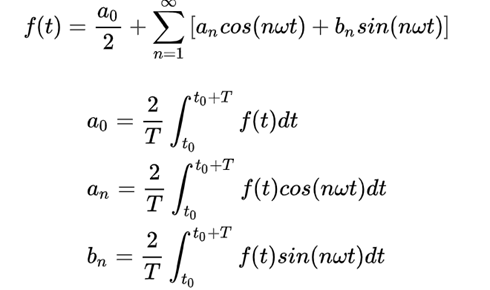
2.2 傅里叶指数形式
(推导见下文的附件二,感兴趣的可以浏览)
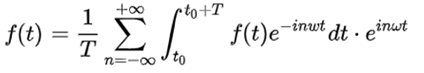
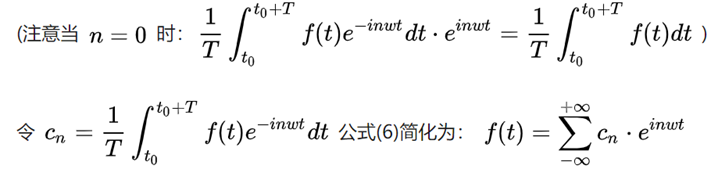
2.3 傅里叶变换和傅里叶逆变化
(推导见下文的附件三,感兴趣的可以浏览)
傅里叶变换:
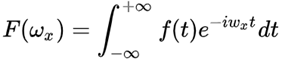
傅里叶逆变换:
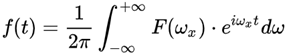
F(ω)叫做f(t)的像函数,f(t)叫做F(ω)的像原函数。F(ω)是f(t)的像。f(t)是F(ω)原像
2.4 离散傅里叶变换和傅里叶逆变化
(推导见下文的附件四,感兴趣的可以浏览)
离散傅里叶变换:
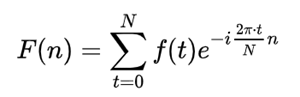
离散傅里叶逆变化
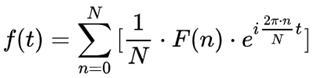
三、傅里叶变换的意义
数字信号处理技术是将声音、图片或者是视频进行信息的模拟再将其转化为数字信息,该技术也是数字时代的标志性技术,目前已经在仪器仪表、通信、计算机以及图像图形处理等领域得到了广泛应用。而数字信号领地最重要的基础就是傅里叶变换,它可分析信号的成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅里叶变换用正弦波作为信号的成分。
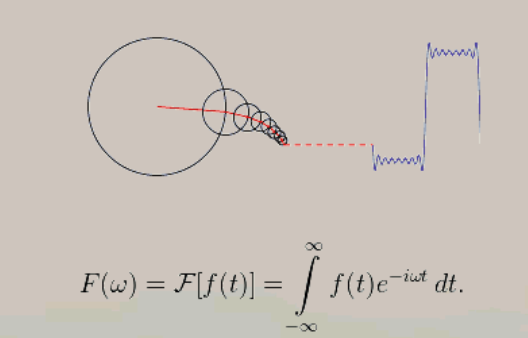
如下图所示:傅立叶变换(的三角函数形式)的基本原理是:多个正余弦波叠加(蓝色)可以用来近似任何一个原始的周期函数(红色)。(如同利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲,也可以看作余弦波叠加成的周期函数)

从时域空间和频域空间看,时域是永远随着时间的变化而变化的,而频域就是装着装着正余弦波的空间:
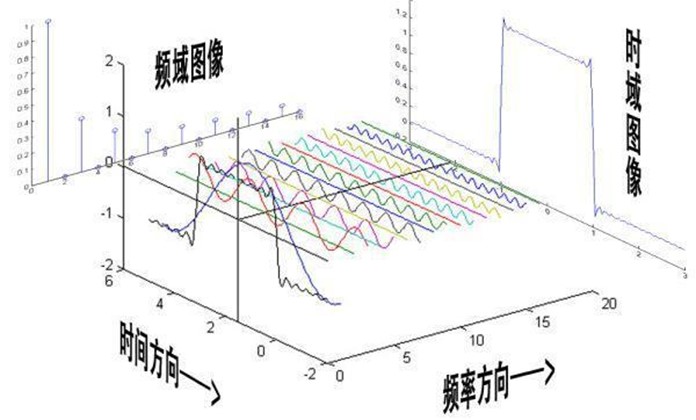
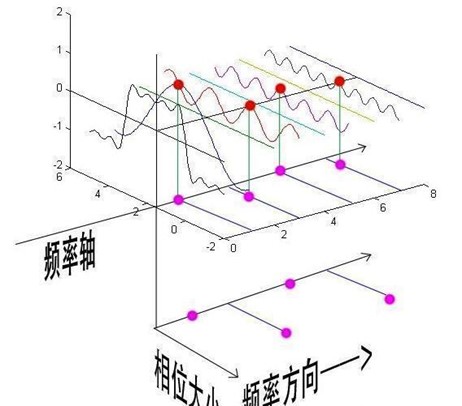
要完整表达曲线,不仅需要频率空间的振幅情况,还需要初始的相位大小,这样就能通过一些点位来确定单个波形的情况,从而拟合出整个时空图像的任意波形。
总结来说:傅立叶变换就是多个正余弦波叠加可以用来近似任何一个原始的周期函数,它实质是是频域函数和时域函数的转换。而其中时域就是永远随着时间的变化而变化的,而频域就是装着装着正余弦波的空间,代表着每一条正余弦波的幅值,而表示正余弦波除了幅值是不够的,就还有相位谱。
附件一:
1、设想可以把一个周期函数f(t)通过最简单的一系列正弦函数来表示
因为正弦函数sin可以说是最简单的周期函数了。于是,傅里叶写出下式:
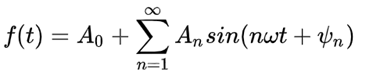
2、通过变形后用三角级数(含sin和cos)来表示
这个n是从1到无穷大,也就是是一个无穷级数,对上式子做变形(来源于高中的三角变换):
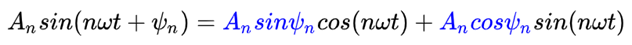
式中,蓝色项即为我们需要合并的常数项,
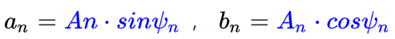
所以傅里叶级数公式得出:
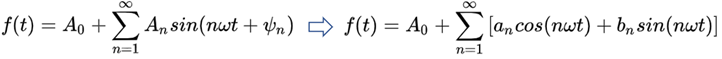
3、通过积分,把各未知系数用f(t)的积分式来表达;
接下来求解A0:
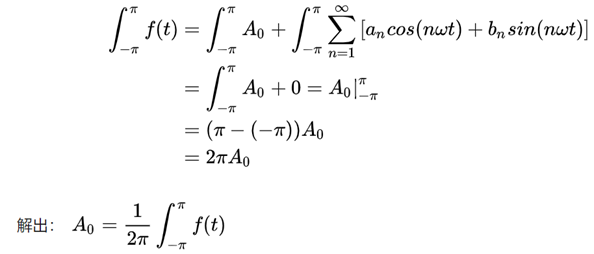
求解an:


同理得出bn:

附件二:
由欧拉公式易知:
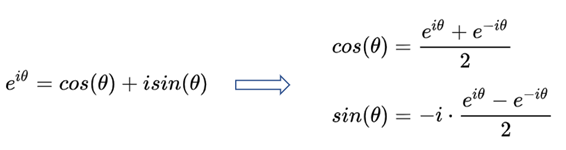
代入傅里叶级数求得:
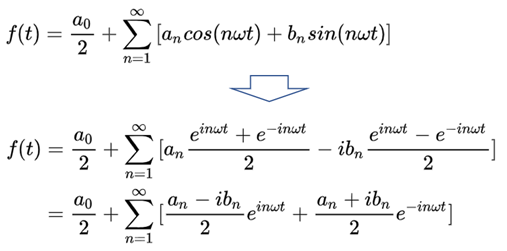
由前面几个表达式得到:
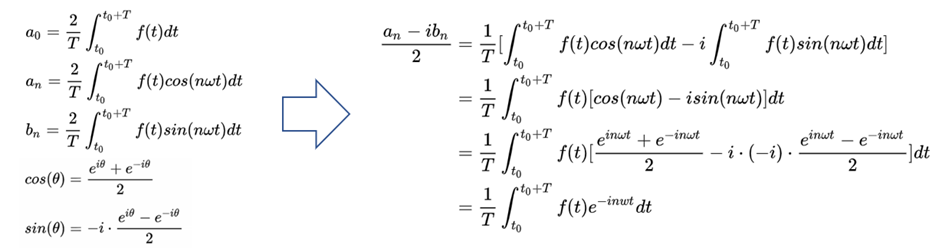
同理可得:

将两式都代入傅里叶级数得到其指数表示:
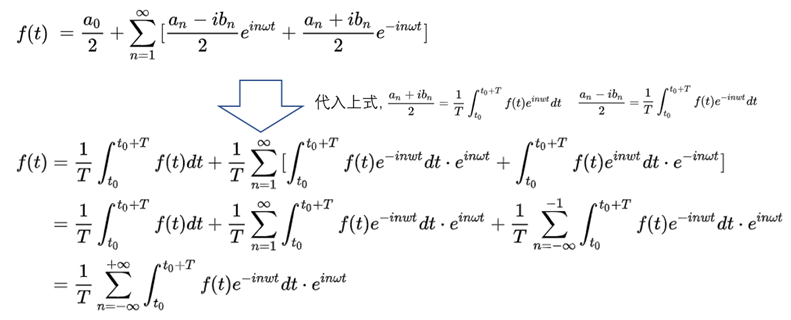
附件三:
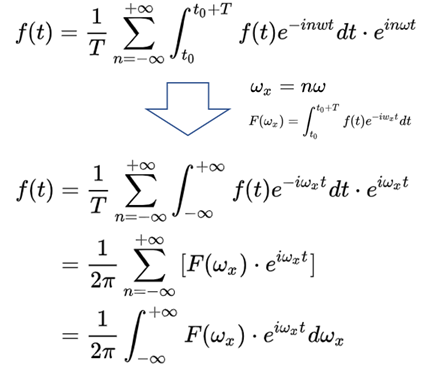
傅里叶变换:
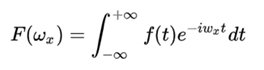
傅里叶逆变换:
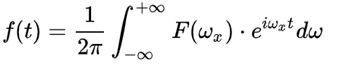
附件四
由附件三知道:
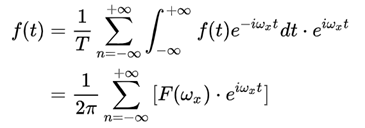
其中:
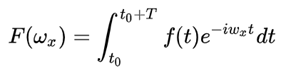

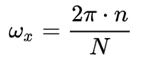
因此我们可以简化公式为
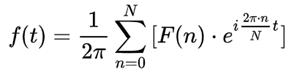
其中:

令N= 2Π,得到如下两个式子:
离散傅里叶变换:
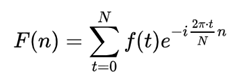
离散傅里叶逆变化
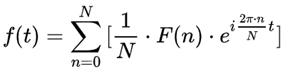
附件五
https://www.bilibili.com/video/av48286796/?redirectFrom=h5 傅里叶的理解视频