目录
- KTT介绍
- KTT的理解
- 内容详解
一、KTT介绍:
KKT条件是泛拉格朗日乘子法的一种形式;主要应用在当我们的优化函数存在不等值约束的情况下的一种最优化求解方式;KKT条件即满足不等式约束情况下的条件:

二、KTT的理解:
可行解必须在约束区域g(x)之内,由图可知可行解x只能在g(x)<0和g(x)=0的区域取得;
1)当可行解x在g(x)<0的区域中的时候,此时直接极小化f(x)即可得到;如下图左;
当可行解在约束内部区域的时候,令β=0即可消去约束。
2)当可行解x在g(x)=0的区域中的时候,此时直接等价于等式约束问题的求解,如下图右。


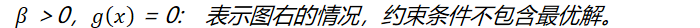
对于参数β的取值而言,在等值约束中,约束函数和目标函数的梯度只要满足平行即可,而在不等式约束中,若β≠0,则说明可行解在约束区域的边界上,这个时候可行解应该尽可能的靠近无约束情况下的解,所以在约束边界上,目标函数的负梯度方向应该远离约束区域朝无约束区域时的解,此时约束函数的梯度方向与目标函数的负梯度方向应相同;从而可以得出β>0。如下图所示:


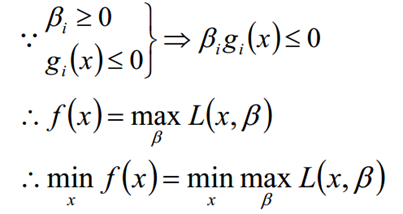

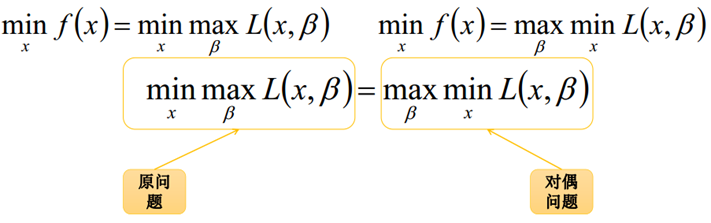
对偶问题的直观理解:最小的里面的那个最大的要比最大的那个里面的最小的大;从而就可以为原问题引入一个下界
另外对偶问题的解,可以参考以下博文:
https://blog.csdn.net/james_616/article/details/72869015
三、KKT条件总结
- 拉格朗日取得可行解的充要条件;
- 将不等式约束转换后的一个约束,称为松弛互补条件;
- 初始的约束条件;
- 初始的约束条件;
- 不等式约束需要满足的条件
