线性回归可以说是机器学习中最基本的问题类型了,这里就对线性回归的原理和算法做一个小结
目录
- 背景
- 简述
- 内容详解
- 密度聚类
- 层次聚类
- 模型效果判断
附件:手写推导过程练习
一、线性回归函数定义


二、线性回归的模型函数和损失函数由来

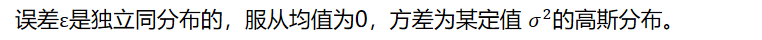
原因:中心极限定理
实际问题中,很多随机现象可以看做众多因素的独立影响的综合反应,往往服从正态分布
从最大似然函数角度出发,是使得最大似然越大越好,假设有m个样本,每个样本对应于n维特征和一个结果输出,如下:
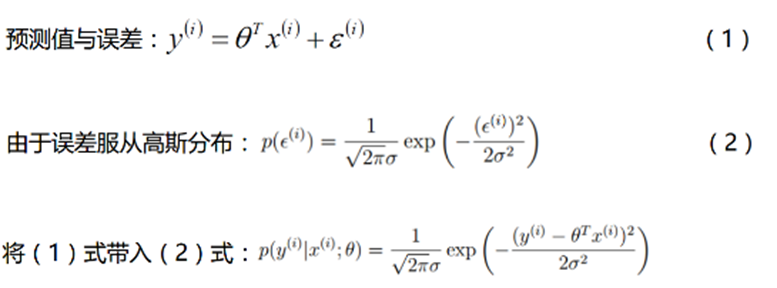

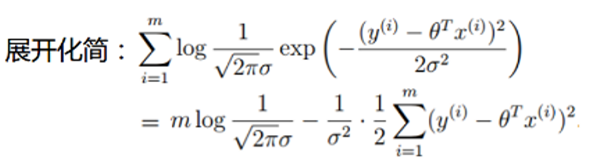
从上面式子的后半部分,要使得上式MAX,即使求解后半部分的MIN。这也和我们的目标减小ε的值,使其最小平方数和最小不谋而合:


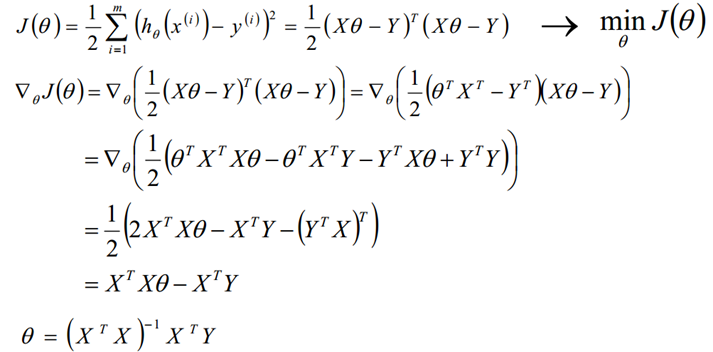
由于矩阵法表达比较的简洁,后面我们将统一采用矩阵方式表达模型函数和损失函数。
二、最小二乘法
参数解析式:
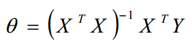


最小二乘法直接求解的难点:矩阵逆的求解是一个难处
具体可见另一篇文章: 最小二乘法(least squares)介绍
当然线性回归,还有其他的常用算法,比如牛顿法和拟牛顿法,这里不详细描述。
三、 线性回归的推广:多项式回归

四、线性回归的推广:广义线性回归

五、线性回归的正则化(防止过拟合)
为了防止模型的过拟合,我们在建立线性模型的时候经常需要加入正则化项。一般有L1正则化和L2正则化。当然这种方法不是仅仅局限于在线性回归中使用,在后面很多机器学习方法中都有涉及。
使用L2正则的线性回归模型就称为Ridge回归(岭回归)。Ridge回归的求解比较简单,一般用最小二乘法。这里给出用最小二乘法的矩阵推导形式,和普通线性回归类似。
使用L1正则的线性回归模型就称为LASSO回归(Least Absolute Shrinkage andSelection Operator)
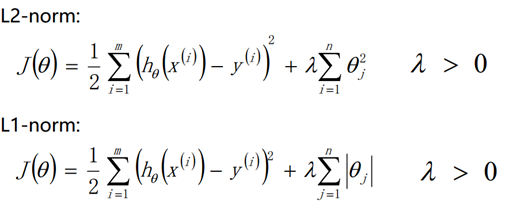
LASSO(L1-norm)和Ridge(L2-norm)比较
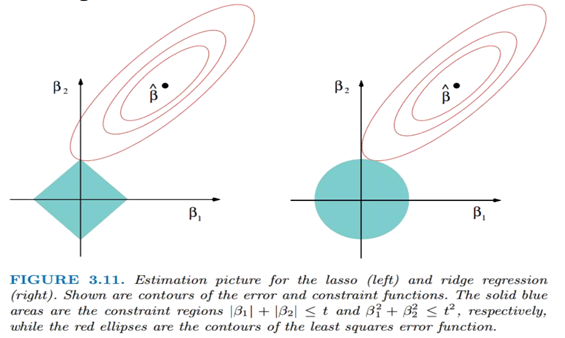
L1很容易产生为0的稀疏矩阵。因为这种情况下更容易交到坐标轴上。
- L2-norm中,由于对于各个维度的参数缩放是在一个圆内缩放的,不可能导致有维度参数变为0的情况,那么也就不会产生稀疏解;实际应用中,数据的维度中是存在噪音和冗余的,稀疏的解可以找到有用的维度并且减少冗余(某些系数的值可以降低为0),提高回归预测的准确性和鲁棒性(减少了overfitting)(L1-norm可以达到最终解的稀疏性的要求)
- Ridge模型具有较高的准确性、鲁棒性以及稳定性;LASSO模型具有较高的求解速度,常用于特征选择,因为可以降低特征数量。
- 如果既要考虑稳定性也考虑求解的速度,就使用Elasitc Net同时使用L1正则和L2正则的线性回归模型就称为Elasitc Net算法(弹性网络算法)
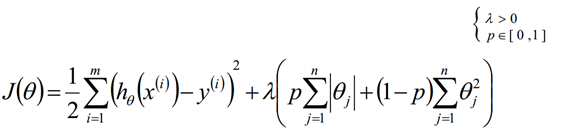
总之:一般使用L2,除非希望得到系数解
六、模型效果判断
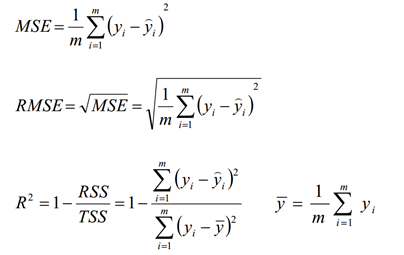
- MSE:误差平方和,越趋近于0表示模型越拟合训练数据。
- RMSE:MSE的平方根,作用同MSE
- R2:取值范围(负无穷,1],值越大表示模型越拟合训练数据;最优解是1;当模型预测为随机值的时候,有可能为负;若预测值恒为样本期望,R2为0
- TSS:总平方和TSS(Total Sum of Squares),表示样本之间的差异情况,是伪方差的m倍
- RSS:残差平方和RSS(Residual Sum of Squares),表示预测值和样本值之间的差异情况,是MSE的m倍
七、总结
- 算法模型:线性回归(Linear)、岭回归(Ridge)、LASSO回归、Elastic Net
- 正则化:L1-norm、L2-norm
-
损失函数/目标函数

- θ求解方式:最小二乘法(直接计算,目标函数是平方和损失函数)、梯度下降(BGD\SGD\MBGD)--请看后面的【2】和【3】