一、目录
1、目录
2、简述
3、CNN的结构组成
4、卷积神经网络 VS. 传统神经网络
5、总结
常见问答
二、简述
1980年,一位名为Fukushima的研究员提出了一种分层神经网络模型。他称之为新认知。该模型的灵感来自简单和复杂细胞的概念。neocognitron能够通过了解物体的形状来识别模式。
后来,1998年,卷心神经网络被Bengio,Le Cun,Bottou和Haffner引入。他们的第一个卷积神经网络称为LeNet-5,能够对手写数字中的数字进行分类。
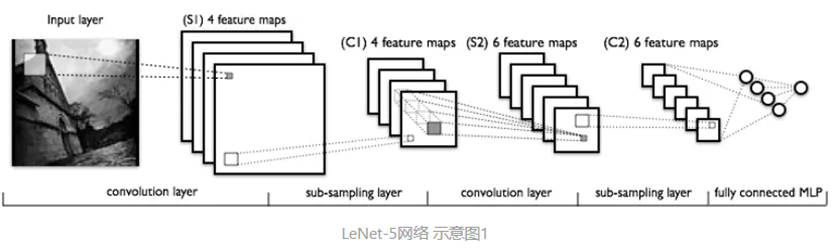
卷积神经网络(Convolutional Neural Network,CNN)是一种前馈神经网络,它的人工神经元可以响应一部分覆盖范围内的周围单元,对于语音识别,时间序列模型和大型图像处理均有出色表现(一维卷积神经网络主要用于序列类的数据处理,二维卷积神经网络常应用于图像类文本的识别,三维卷积神经网络主要应用于医学图像以及视频类数据识别。)。 它包括输入层、卷积层、激活函数、池化层、全连接层。CNN的概念图如下:
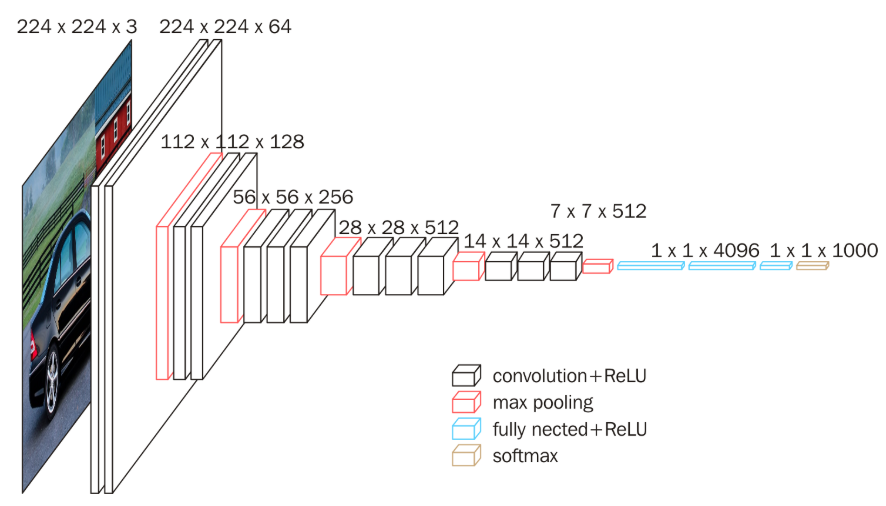
上图为VGG16的网络结构,共16层(不包括池化和softmax层),所有的卷积核都使用3*3的大小,池化都使用大小为2*2,步长为2的最大池化,卷积层深度依次为64 -> 128 -> 256 -> 512 ->512。
CNN架构简单来说就是:图片经过若干次的Convolution, Pooling, Fully Connected就是CNN的架构了,因此只要搞懂Convolution, Pooling, Fully Connected三个部分是核心。本文以房颤鉴别实验作介绍(使用tensorflow)
三、CNN的结构组成
3.1 Convolutional layer(卷积层--CONV)
卷积层是卷积神经网络的核心基石。在图像识别里我们提到的卷积是二维卷积,即离散二维滤波器(也称作卷积核)与二维图像做卷积操作,简单的讲是二维滤波器滑动到二维图像上所有位置,并在每个位置上与该像素点及其领域像素点做内积。不同卷积核可以提取不同的特征,例如边沿、线性、角等特征。在深层卷积神经网络中,通过卷积操作可以提取出图像低级到复杂的特征。在一维数组中,用于提取极值等特征。卷积核的权重是可以学习的,由此可以猜测,在高层神经网络中,卷积操作能突破传统滤波器的限制,根据目标函数提取出想要的特征。
由滤波器filters和激活函数构成。一般要设置的超参数包括filters的数量、大小、步长,以及padding是"valid"还是"same"。当然,还包括选择什么激活函数。
卷积运算就是将原始图片的与特定的Feature Detector(filter)做卷积运算(符号⊗),卷积运算就是将下图两个3x3的矩阵作相乘后再相加,以下图为例0 *0 + 0*0 + 0*1+ 0*1 + 1 *0 + 0*0 + 0*0 + 0*1 + 0*1 =0

再举一个例子:我们有下面这个绿色的5x5输入矩阵,卷积核是一个下面这个黄色的3x3的矩阵。卷积的步幅是一个像素。则卷积的过程如下面的动图。卷积的结果是一个3x3的矩阵

在斯坦福大学的cs231n的课程上,有一个动态的例子,链接。建议大家对照着例子中的动图看下面的讲解。
常见的激活函数如下,详细的可移步到我机器学习的另一篇文章。
|
类型 |
sigmoid |
RELU |
Leaky ReLU |
tanh |
|
说明 |
计算量大,容易梯度消失 |
计算简单 |
计算量稍大,一般是RELU不能使用时才启用 |
特征向量明显时效果较好 |
3.2 Pooling layer (池化层--POOL)
池化层:(Pooling Layer,POOL ):保证特不变性,降低维度,减少后续计算量,一定程度上防止过拟合。池化层进行的运算一般有以下几种:
|
类型 |
最大池化(Max Pooling) |
均值池化(Mean Pooling) |
高斯池化 |
|
说明 |
取几个点中最大的 |
取几个数的均值 |
借鉴高斯模糊的方法,不常用 |
需要指定的超参数,包括是Max还是average,窗口大小以及步长。
通常,我们使用的比较多的是Maxpooling,而且一般取大小为(2,2)步长为2的filter,这样,经过pooling之后,输入的长宽都会缩小2倍,channels不变。
下面这个例子采用取最大值的池化方法。同时采用的是2x2的池化。步幅为2(这是压缩的关键)。首先对红色2x2区域进行池化,由于此2x2区域的最大值为6.那么对应的池化输出位置的值为6,由于步幅为2,此时移动到绿色的位置去进行池化,输出的最大值为8.同样的方法,可以得到黄色区域和蓝色区域的输出值。最终,我们的输入4x4的矩阵在池化后变成了2x2的矩阵。进行了压缩。

3.3 Fully Connected layer(全连接层--FC)
这个前面没有讲,是因为这个就是我们最熟悉的家伙,就是我们之前学的神经网络中的那种最普通的层,就是一排神经元。因为这一层是每一个单元都和前一层的每一个单元相连接,所以称之为"全连接"。
这里要指定的超参数,无非就是神经元的数量,以及激活函数。
四、卷积神经网络 VS. 传统神经网络
传统的神经网络,其实就是多个FC层叠加起来。CNN,无非就是把FC改成了CONV和POOL,就是把传统的由一个个神经元组成的layer,变成了由filters组成的layer。那么,为什么要这样变?有什么好处?具体说来有两点:
1.参数共享机制(parameters sharing)
我们对比一下传统神经网络的层和由filters构成的CONV层:
假设我们的图像是8×8大小,也就是64个像素,假设我们用一个有9个单元的全连接层:

那这一层我们需要多少个参数呢?需要 64×9 = 576个参数(先不考虑偏置项b)。因为每一个链接都需要一个权重w。
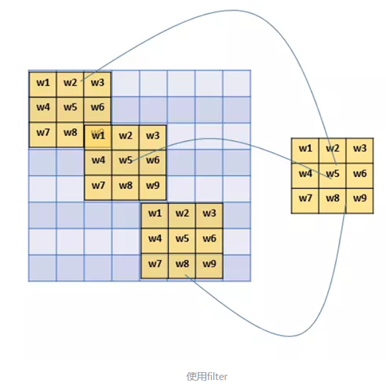
其实不用看就知道,有几个单元就几个参数,所以总共就9个参数!
因为,对于不同的区域,我们都共享同一个filter,因此就共享这同一组参数。通过前面的讲解我们知道,filter是用来检测特征的,那一个特征一般情况下很可能在不止一个地方出现,比如"竖直边界",就可能在一幅图中多出出现,那么 我们共享同一个filter不仅是合理的,而且是应该这么做的。
由此可见,参数共享机制,让我们的网络的参数数量大大地减少。这样,我们可以用较少的参数,训练出更加好的模型,典型的事半功倍,而且可以有效地 避免过拟合。
同样,由于filter的参数共享,即使图片进行了一定的平移操作,我们照样可以识别出特征,这叫做 "平移不变性"。因此,模型就更加稳健了。
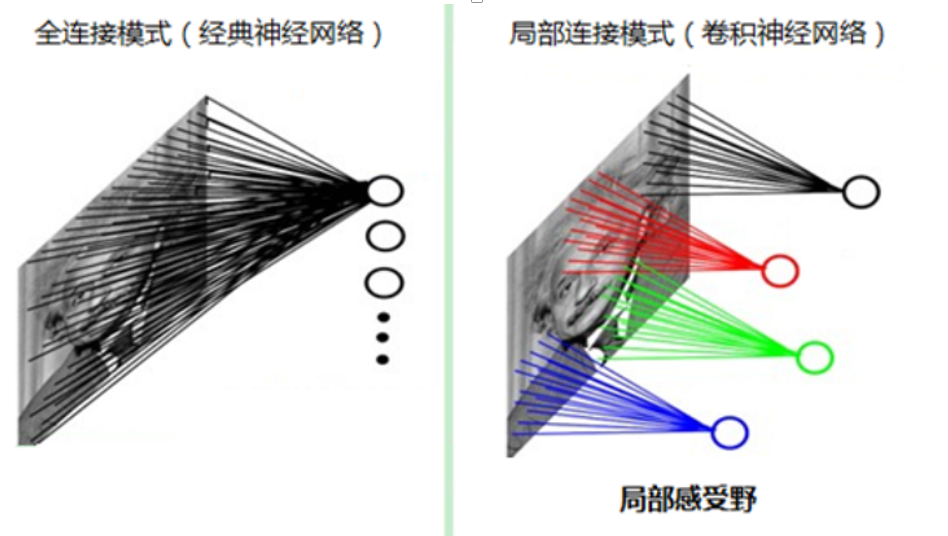
2.局部感受野
如果采用经典的神经网络模型,则需要读取整幅图像作为神经网络模型的输入(即全连接的方式),当图像的尺寸越大时,其连接的参数将变得很多,从而导致计算量非常大,上面1也解释了。
我们人类对外界的认知一般是从局部到全局,先对局部有感知的认识,再逐步对全体有认知,这是人类的认识模式。在图像中的空间联系也是类似,局部范围内的像素之间联系较为紧密,而距离较远的像素则相关性较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。这种模式就是卷积神经网络中降低参数数目的重要神器:局部感受野。
连接的稀疏性(sparsity of connections)中,由卷积的操作可知,输出图像中的任何一个单元,只跟输入图像的一部分有关系。 而传统神经网络中,由于都是全连接,所以输出的任何一个单元,都要受输入的所有的单元的影响。这样无形中会对图像的识别效果大打折扣。比较,每一个区域都有自己的专属特征,我们不希望它受到其他区域的影响。
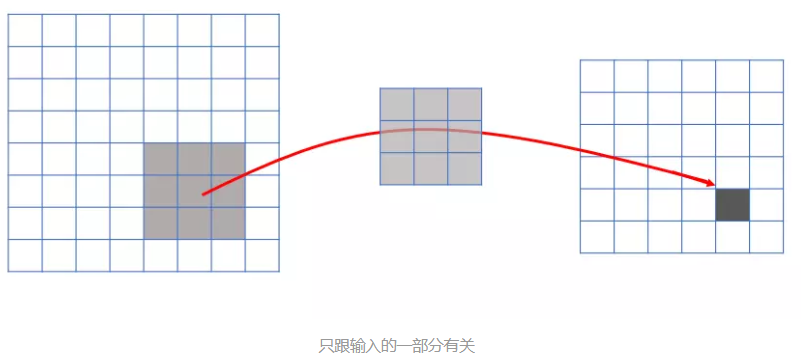
正是由于上面这两大优势,使得CNN超越了传统的NN,开启了神经网络的新时代。
五、总结
根据经典的手写识别LeNet5再进一步阐述过程:
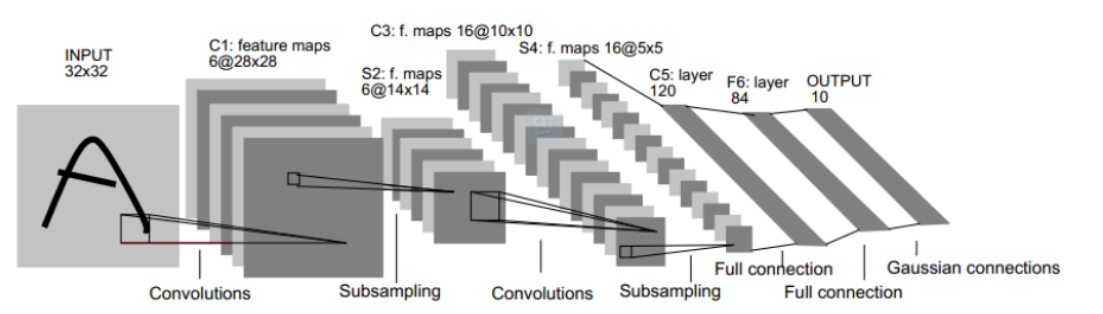
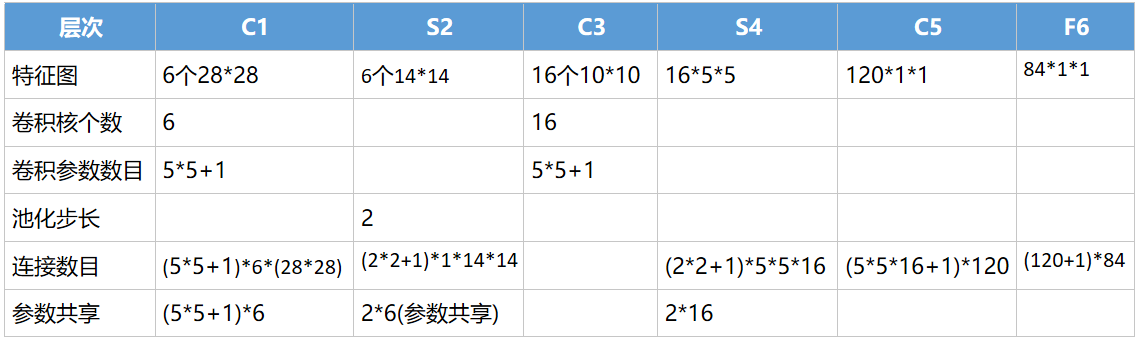
C3的每个特征图中的每个元素由S2中某几层多个5*5的领域相连
S4每张特征图需要一个因子和一个偏置量,共2个参数
最后输出层采用欧式径向基函数(Euclidean Radial Basis Function)
常见问答:
关于卷积的计算:

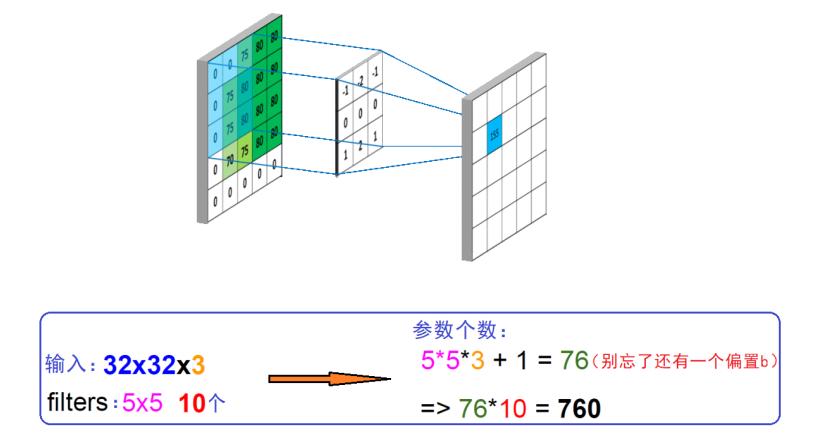
共享权值数量计算:
参考文献:
https://www.cnblogs.com/wj-1314/p/9754072.html