1.【算法】单调栈
参考:https://blog.csdn.net/lucky52529/article/details/89155694
一、算法理解
单调栈是一种理解起来很容易,但是运用起来并不那么简单的数据结构。
单调栈,就是一个堆栈,里面的元素的按照大小在栈中满足一定的单调性。也就说是,就是递增存储元素、或递减存储元素,当该单调性(递增性、或递减性)被打破时要进行适当出栈。
单调栈也分为 递增单调栈 和 递减单调栈
- 递增单调栈:从栈底 到 栈顶 保存的数据是从小到大
- 递减单调栈:从栈底 到 栈顶 保存的数据是从大到小
【举例】:
数据序列[10, 7, 6, 8, 5, 9, 3]在 递减单调栈 中的出栈、入栈顺序为:
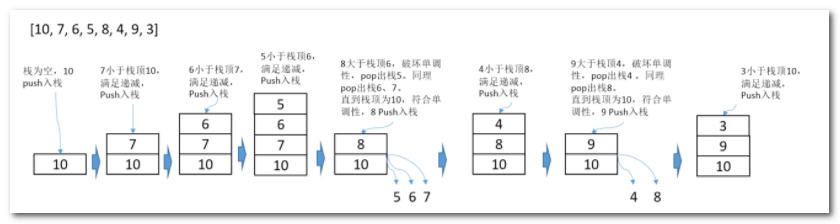
通过样例可以看出,对于递减单调栈:
- 最大数据一定在栈中(未出栈)
- 栈中最终残余参数是递减
【伪码】:
单调栈( 单调递减 为例)的伪码如下:
stack<int> st;
for (遍历集合中元素)
{
if (栈空 || 栈顶元素 >= 当前元素)
{
入栈;
}
else
{
while (栈不为空 && 栈顶元素 < 当前元素)
{
栈顶元素出栈;
根据业务场景计算结果;
}
当前元素入栈;
}
}
【以一个例子加深理解】:
N个人排队,给出每个人身高,所有的人全部向右看,个子高的可以看到个子低的发型,问:序列中一共可以看到多个个人的发型。
把身高换成成柱图,如下:
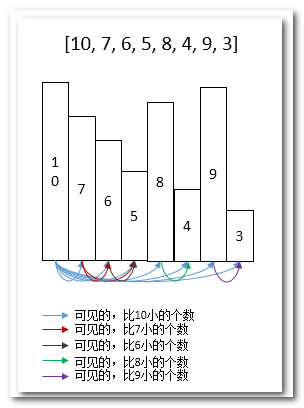
按照如上算法迭代过程,如何确定业务场景计算结果公式呢?
- 如图:7能看到6/5,6能看到5,根据单调栈规律如何计算:8右边的内容,即便是小于7,7/6/5也是看不到的。按照单调栈前面伪码,8破坏单调栈递减规律,触发出栈。
- 8触发出栈,和业务计算公式啥关系呢?标注上index数组下表,可能更清楚一点:
- 5向右能看到的个数0
- 6向右能看到的index=3的元素
- 7向右能看到的是index=2、index=3的元素
- 看到规律了吧,5、6、7能看到的元素个数就是:其index 到 单调栈破坏点8(index=4)之间的间隔数。
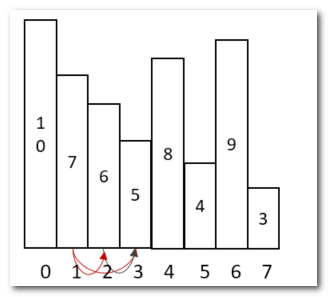
换算成单调栈伪码的出栈出发逻辑就是:
- 5出栈时,5向右能看到的发型数量:4(index of 8) - 3(index of 5) -1
- 6出栈时,6向右能看到的发型数量:4(index of 8) - 2(index of 6) -1
- 7出栈时,7向右能看到的发型数量:4(index of 8) - 1(index of 7) -1
......
[注]:按照如上规律遍历完队列后,元素遍历完毕后,栈中还有元素的。剩余这些元素,在队列中其右边没有比其更大的元素。换言之:剩余每个元素能看到其右边所有元素的发型。
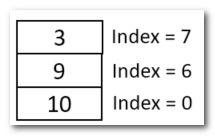
【针对参与元素调整后的伪码】
调整方式一:在原始数组最后加一个超大元素,确保所有元素出栈
元素列表末尾位置添加一个Max元素; //Here
for (遍历集合中元素)
{
if (栈空 || 栈顶元素 >= 当前元素)
{
入栈;
}
else
{
while (栈不为空 && 栈顶元素 < 当前元素)
{
栈顶元素出栈;
总数 += 当前元素index - 栈顶出栈元素index - 1;
}
当前数据入栈;
}
}
调整方式二:单调处理完毕后,栈内残余元素出栈
for (遍历集合中元素)
{
if (栈空 || 栈顶元素 >= 当前元素)
{
入栈;
}
else
{
while (栈不为空 && 栈顶元素 < 当前元素)
{
栈顶元素出栈;
总数 += 当前元素index - 栈顶出栈元素index - 1; //Here
}
当前数据入栈;
}
}
//剩余元素出栈
while (栈不为空) //Here
{
栈顶元素出栈;
总数 += 队列最大index - 栈顶出栈元素index;
}
二、适用场景
按照单调栈(以递减单调栈为例)规律:
- 最大元素一定在栈中(未出栈)
- 栈中最终残余元素是递减
基于单调栈的特点,单调栈可以用于:
[预置输入]:
- 未排序序列
- 单向比较(向左看、向右看)。(备注:如果双向,可分解为向右一次单调栈、向左一次单调栈)
- 比较元素间大小规律
[目标输出]: - 寻找序列最大(小)值
- 筛选并处理序列中不符合递减/递增规律的元素。如:
- 筛选一定规律的子序列并处理(坡的最大宽度场景);
- 计算某规律下元素之间间距相关的等。
三、使用注意事项
单调栈能很好的对一组元素的峰、谷进行筛选处理,遇到和峰谷相关的场景,可以考虑用单调栈算法。
单调栈使用中思路和注意实现:
- 确认方向(左->右? 右->左?)
- 确认栈类型(递增/递减单调栈)
- 递增单调栈:大数为出栈触发点,小数出栈;最终栈内数据一定包含最大 那个数。
- 递减单调栈:小数为出栈触发点,大数出栈;最终栈内数据一定包含最小那个数。
- 业务目标结果与栈的关系(与出栈元素有关 ;与栈内**残余数据 **有关)
- 业务与逐个元素有关,一般选择与出栈元素有关。(如:矩形面积、接雨水)
- 业务与序列最大/小元素有关,一般选择与残余数据关联。(如滑窗内最大值)
- 业务是与 出栈数据/残余数据 有关,数据 找大/找小,决定了使用递增/递减单调栈。
遇到单调栈解决问题的业务场景,先根据单调栈特点建业务模型:
- 业务和单调栈关联模型:注意
- 选择关联合适的触发出栈点index、出栈元素index、出栈前、后元素index。
- 如有需要,可以入栈时调整index、原始数据。(如:计算矩形面积案例)
- 相等元素处理策略:触发出栈处理、还是入栈处理。
- 残余数据处理策略:根据不同业务,考虑最终栈内残余单向元素是否需要出栈处理。
四、使用案例
1. [1类]单向找下一个更大/更小元素
1)看发型(下一个更高人)
如算法理解章节描述。其代码实现如下:
(1)对应代码【伪码1方式】
public int FieldSum(ArrayList<Integer> personList) {
personList.add(Integer.MAX_VALUE);
ArrayDeque<Integer> stack = new ArrayDeque<Integer>(personList.size() + 1);
int sum = 0;
for (int i = 0; i < (int)personList.size(); i++) {
//小于栈顶元素入栈
if (stack.isEmpty() || personList.get(stack.peekLast()) > personList.get(i)) {
stack.addLast(i);
} else {
while (!stack.isEmpty() && personList.get(stack.peekLast()) <= personList.get(i)) {
int top = stack.pollLast(); //取出栈顶元素
sum += (i - top - 1); //这里需要多减一个1
}
stack.addLast(i);
}
}
return sum;
}
(2)调整后的伪码2-对应代码
public int FieldSum(int[] personList) {
ArrayDeque<Integer> stack = new ArrayDeque<Integer>(personList.length + 1);
int sum = 0;
for (int i = 0; i < (int)personList.length; i++) {
//小于栈顶元素入栈
if (stack.isEmpty() || personList[stack.peekLast()] > personList[i]) {
stack.addLast(i);
} else {
while (!stack.isEmpty() && personList[stack.peekLast()] <= personList[i]) {
int top = stack.pollLast(); //取出栈顶元素
sum += (i - top - 1); //这里需要多减一个1
}
stack.addLast(i);
}
}
while (!stack.isEmpty()) {
int top1 = stack.pollLast(); //取出栈顶元素
sum += (personList.length - top1 - 1); //这里需要多减一个1
}
return sum;
}
2)下一个更大元素间距
给定一个数组,返回一个大小相同的数组。返回的数组的第i个位置的值,是原数组中的第i个元素,至少往右走多少步,才能遇到一个比自己大的元素(如果之后没有比自己大的元素,或者已经是最后一个元素,则在返回数组的对应位置放上-1)。
样例:
输入: 5, 3, 1, 2, 4
输出: -1 3 1 1 -1
【思路】
[输入]无序序列、找大小。同看发型,找间距一样用单调栈。
- 方向:左到右
- 业务逻辑:
如,7到8的距离,应该是index[4]-index[1],填充到新数组的index[1]位置。
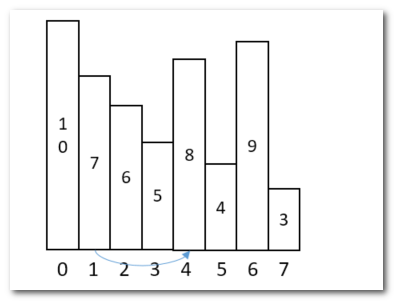
- 非法位置是-1,可以把数组默认设置为-1。
- 残余数据:由于最终单调栈中剩余的递减元素,不影响返回的数组,不需要出栈。
- 相等的值:由于是找下一个
代码实现参考:
public static int[] FieldSum(int[] list)
{
ArrayDeque<Integer> stack = new ArrayDeque<Integer>(list.length + 1);
int[] restList = new int[list.length];
Arrays.fill(restList, -1);
for (int i = 0; i < (int)list.length; i++) {
//小于栈顶元素入栈
if (stack.isEmpty() || list[stack.peekLast()] >= list[i]) {
stack.addLast(i);
} else {
while (!stack.isEmpty() && list[stack.peekLast()] < list[i]) {
int top = stack.pollLast(); //取出栈顶元素
restList[top] = (i - top);
}
stack.addLast(i);
}
}
return restList;
}
3)股价跨度
已知某支股票的每日报价,返回该股票当日价格的跨度。今天股票价格跨度被定义为股票价格小于或等于今天价格的最大连续日数(从今天开始往回数,包括今天)。
例如,如果未来7天股票的价格是 [100, 80, 60, 70, 60, 75, 85],那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。
【思路】:
- 栈类型:单向、下一个更大值;从右向左边。
- 业务公式:出栈时,value = TopIndex - CurIndex。
- 残余数据:残余数据递减,需全部出栈。
2. [2类]循环下一个更大/更小元素
1)下一个更大元素(循环)
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素)。输出:每个元素的下一个更大元素。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
【思路】:
- 栈类型:找下一个更大元素,使用 递减 单调栈,方向 向右。
- 业务公式:由于是向右循环,某个[Index]向右到队列末尾找不到,继续循环从队列头找,第二次遍历对立依然找不到,就可以结束。所以考虑把[1,2,1]--> [1, 2, 1, 1, 2, 1] 循环两次进行单调栈,返回的结果数组只需记录[0]~[2]的数据即可。
- 残余数据:找下一个更大元素的值,残余数据是递减顺序,无需处理。
模型化就是:
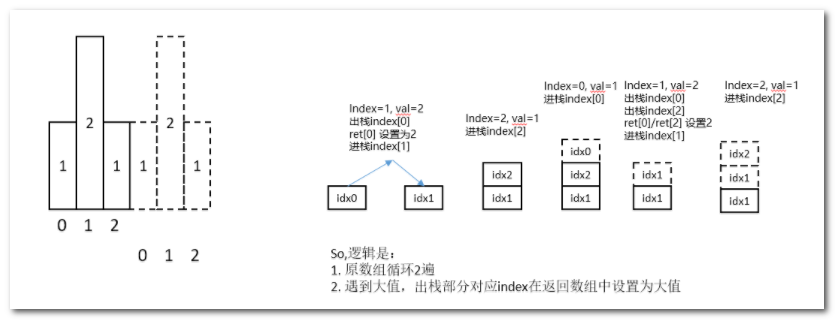
实现代码参考:
public static int[] nextGreaterElements(int[] nums) {
if (nums == null || nums.length == 0) {
return new int[0];
}
int[] retList = new int[nums.length];
Arrays.fill(retList, -1);
ArrayDeque<Integer> stack = new ArrayDeque<Integer>(2 * nums.length);
for (int i = 0; i < 2 * nums.length; i++) {
int index = i % nums.length;
if (stack.isEmpty() || nums[stack.peekLast()] >= nums[index]) {
stack.addLast(index);
} else {
while (!stack.isEmpty() && nums[stack.peekLast()] < nums[index]) {
int top = stack.pollLast();
retList[top] = nums[index];
}
stack.addLast(index);
}
}
return retList;
}
3. [3类]利用下一个更大/更小元素复杂计算
1)柱状图中的最大矩形
给定一个非负整数序列,表示柱状图中各个柱子的高度,每个柱子想邻,且宽度都为1。
求柱状图中,能勾勒的最大矩形面积。
我们用图形化建模,来理顺业务逻辑,如下:
- 栈类型:采用递增单调栈,遇到更小元素,计算前面的面积值。
- 残余元素:注意最后一个元素在所有柱状图中最小,需要按照数组全部length计算面积。
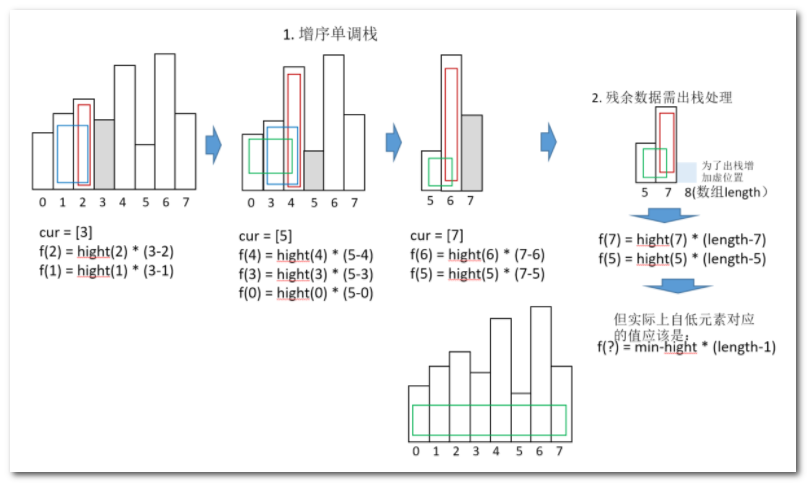
按照如上建模,得出的业务逻辑是否正确呢?继续分析。
- 以3为为例,我们按照如上逻辑,在2出栈时,计算的最大面积是:
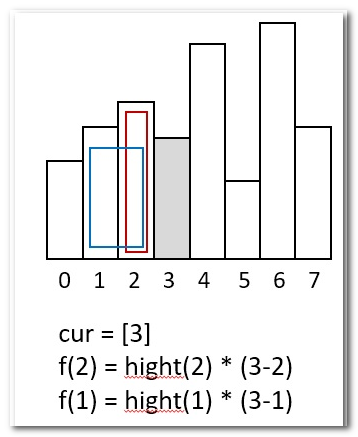
- 但实际上,从完整的柱图看,采用hight(3)高度的最大面积是:
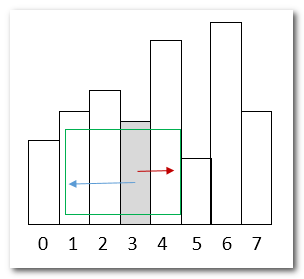
为什么这种情况呢?因为:
单调栈常规的出栈时,个数/距离计算的是出栈index[3] 单向到 触发点index[5] 之间距离,如上图红色箭头部分。相反方向(蓝色箭头部分)是没有计算的。那么怎么解决这个问题呢?
我们考虑在(3)入栈时,把其 index 刷新为最后出栈的索引(出栈的元素hight都大于hight(3),可以被hight(3)计算面积)。过程如下:
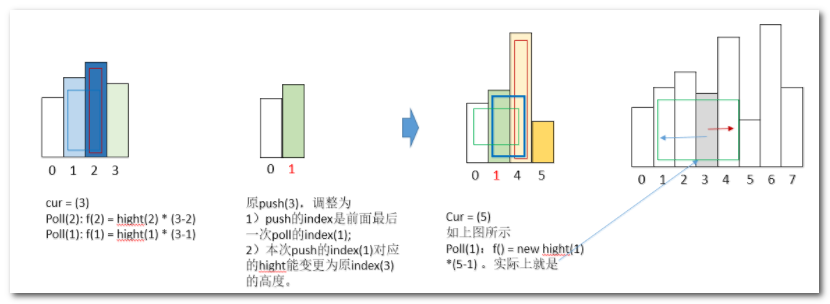
在入栈(3)的时候实际上做了两件事:
- 变更单调栈入栈的index,为前面最后一出栈的Index(即向前最靠前一个高于(3)的柱子的index)。
- 调整真正入栈的index对应的hight为(3)的高度。
- 目的是让下次index(1)出栈计算时,使用原始预期的higth(3)的值。
- 原始index(1)对应的面积,在遇到cur=3时已经计算过,对其higth的更改,本质上不会有影响。
按照此最新逻辑,则图形化建模如下:
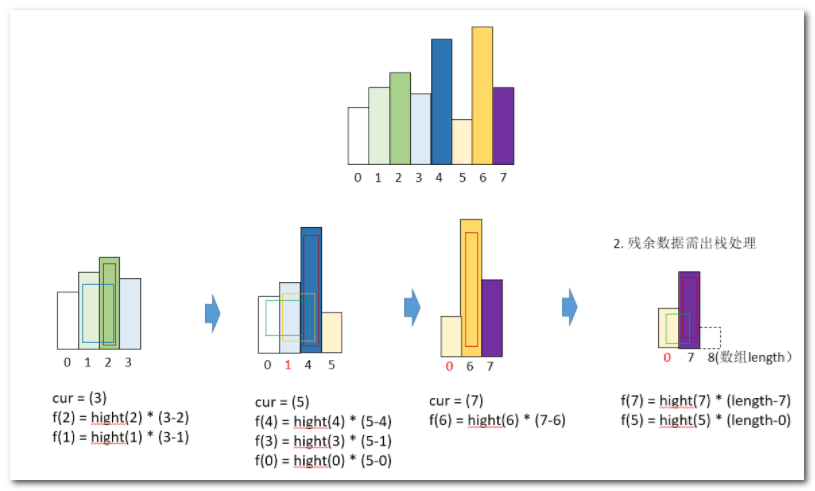
代码如下:
public static int FieldSum(int[] list) {
ArrayDeque<Integer> stack = new ArrayDeque<Integer>(list.length + 1);
int maxArea = 0;
int top = 0;
for (int i = 0; i < (int) list.length; i++) {
//小于栈顶元素入栈
if (stack.isEmpty() || list[stack.peekLast()] <= list[i]) {
stack.addLast(i);
} else {
while (!stack.isEmpty() && list[stack.peekLast()] > list[i]) {
top = stack.pollLast();//取出栈顶元素
//出栈a
maxArea = Math.max(maxArea, list[top] * (i - top));
}
//重要!!!!注意这里
//stack.addLast(i);
stack.addLast(top);
list[top] = list[i];
}
}
while (!stack.isEmpty()) {
top = stack.pollLast();//取出栈顶元素
maxArea = Math.max(maxArea, list[top] * (list.length - top));
}
return maxArea;
}
PS:本题目还可以考虑使用滑窗算法:
- 从滑窗中找到最低点,计算 滑窗长度 x 最低点高度。
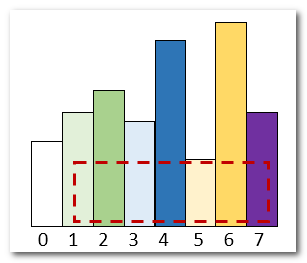
2)接雨水
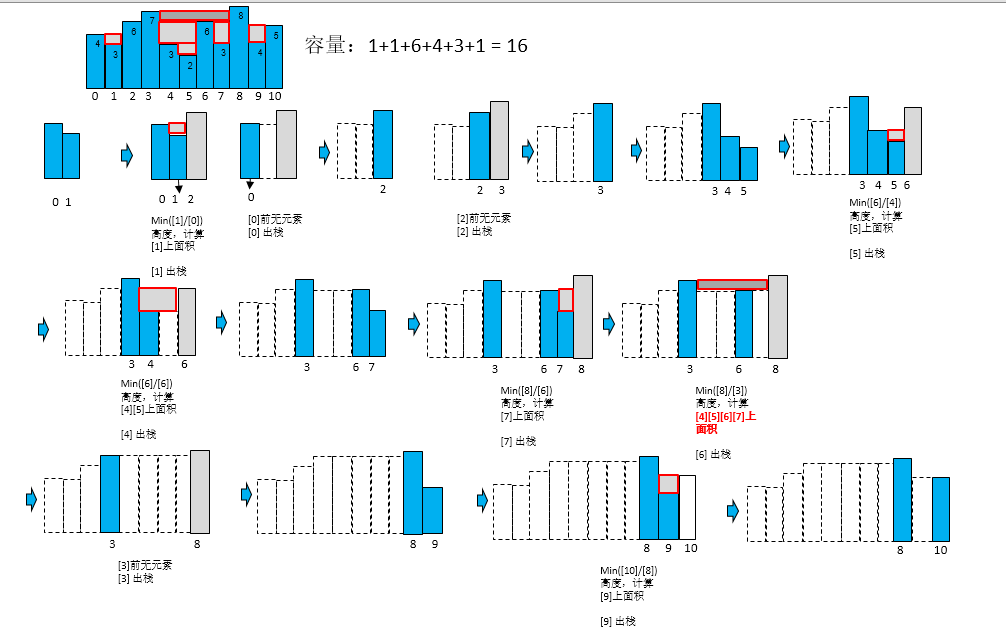
【分析】
- 栈类型:向右单项,遇大值出栈(递减单调栈)。
- 业务公式:
- 出栈时,计算Cur(触发出栈元素) 和 出栈元素的前一元素 Min高度,作为当前出栈元素补齐面积的高。(出栈前是递减栈,一定存在高度差)
- 计算出栈时补齐面积的宽度:出栈7之前,其宽度计算规律都是cur的[index]-poll的[index]。但是出栈6时发现这个规律不正确了;6前面作为触发出栈的元素,导致6前面有很多空间,其补齐后高度是与6相同的。So:宽度计算公式,也变更为以出栈元素前一元素为基准: curIndex - 出栈前一元素Index(先poll,再peek) - 1;
- 总面积 = Sum(1.2.中计算的增补面积)
- 残余数据:不需处理
参考代码:
ArrayDeque<Integer> stack = new ArrayDeque<Integer>(height.length);
int Area = 0;
for (int i = 0; i < height.length; i++) {
//小于栈顶元素入栈
if (stack.isEmpty() || height[stack.peekLast()] >= height[i]) {
stack.addLast(i);
} else {
while (!stack.isEmpty() && height[stack.peekLast()] < height[i]) {
int top = stack.pollLast(); //取出栈顶元素
if (!stack.isEmpty()) {
int pre = stack.peekLast();
int hight = Math.min(height[i], height[pre]) - height[top];
Area += hight * (i - pre - 1);
}
}
stack.addLast(i);
}
}
return Area;
}
3)矩阵中最大面积
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
输出: 6
逐行为底座,把矩阵连续的1看成一个个柱状图,采用矩阵面积的方式期求解。
代码参考:
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0) {
return 0;
}
int[] heights = new int[matrix[0].length];
int maxArea = 0;
for (int row = 0; row < matrix.length; row++) {
//遍历每一列,更新高度
for (int col = 0; col < matrix[0].length; col++) {
if (matrix[row][col] == '1') {
heights[col] += 1;
} else {
heights[col] = 0;
}
}
//调用上一题的解法,更新函数
maxArea = Math.max(maxArea, largestRectangleArea(heights));
}
return maxArea;
}
4. [4类]利用残余数据包含最大/最小值
1)滑窗最大值
给你一个整数序列nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧,滑动窗口每次只向右移动一位,返回滑动窗口中的最大值。
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
【解析】
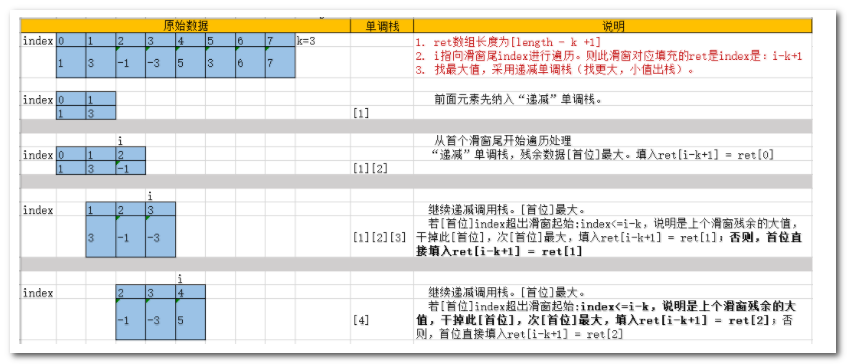
- 方向:向右单向
- 栈类型:递减单调栈。小值出栈,残余数据保留Top,且大值在首位。
- 业务逻辑:如上图。
- 残余数据:根据业务逻辑,不需出栈,查询首元素即可。
代码参考:
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0) {
return new int[0];
}
int length = nums.length;
//返回结果能记录到最后一个滑窗首index即可。
int[] array = new int[length - k + 1];
ArrayDeque<Integer> queue = new ArrayDeque<>();
//第一个滑窗末位前数据入栈,递减栈-小值除栈,留栈是大值,且最大值首位
for (int i = 0; i < (k - 1); i++) {
while (!queue.isEmpty() && nums[i] > nums[queue.peekLast()]) {
queue.pollLast();
}
queue.addLast(i);
}
//从首个滑窗末位为i,开始逐个单元向后移动滑窗
for (int i = k - 1; i < length; i++) {
while (!queue.isEmpty() && nums[i] > nums[queue.peekLast()]) {
queue.pollLast();
}
queue.addLast(i);
//单调站[首位]最大值超出当前滑窗范围,说明是上个滑窗的值,删除。次[首位]变更当前滑窗最大值。
if (i - queue.peekFirst() >= k) {
queue.removeFirst();
}
//[首位]最大值纳入返回数组
array[i - k + 1] = nums[queue.peekFirst()];
}
return array;
}
5. [5类]利用筛选单向元素序列(严格来说,不是单调栈)
2)坡的最大宽度
给定一个整数数组A。坡是元组 (i, j),其中 i < j 且 A[i] <= A[j],这样的坡的宽度为 j - i。找出 A 中的坡的最大宽度,如果不存在,返回 0 。
输入:[6,0,8,2,1,5]
输出:4
解释:最大宽度的坡为 (i, j) = (1, 5): A[1] = 0 且 A[5] = 5.
【暴力破解法】
public int maxWidthRamp(int[] A) {
int ans = 0;
int length = A.length;
for(int j = 0; j < length ; j++) {
for(int k = j + 1; k< length;k ++) {
if(A[k] >= A[j]) {
ans = Math.max(ans, k - j);
}
}
}
return ans;
}
如上,直接暴力循环遍历,结果提示时间超时。
如下:优化一下,ans保存的是索引间最大距离。双层for循环遍历时,外层循环中最后的ans个元素(ans - length)不需要再用i遍历了,因为i在此范围内向后遍历k,i和k之间的差值不可能>ans。
public int maxWidthRamp(int[] A) {
int ans = 0;
int length = A.length;
for(int j = 0; j < length - ans ; j++) {
for(int k = j + 1; k< length;k ++) {
if(A[k] >= A[j]) {
ans = Math.max(ans, k - j);
}
}
}
return ans;
}
【采用单调栈方法】
以为例:[6,1,0,7,2,8,1,5] ,图形化展示:
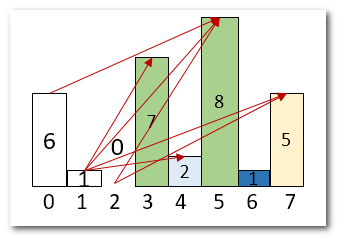
可以看到,最大坡度在红线之间比较选择。
为什么78、28、25、15的坡度忽略了呢?因为在这些元素前,都出现过比其小的元素,“其到后面x的坡度” 不可能大于 “前面比其小的元素 到x的坡度”。
So:
从6开始,只找递减的元素。然后序列从尾到头,和这些元素比较,获取最大值。
这里就用到递减单调栈。因为业务使用的是残余元素,不符合递减规律的元素不需要进栈、出栈、直接忽略。
本样例,筛选后栈内数据是(记录index):[0, 1, 2],然后把队列从尾向前遍历,和单调栈中记录的元素比较即可。
比较时,如上图:05的距离,肯定大于08的距离,所以,比5小的元素只需和5比较就好,不需在和前面的8比较。所以边比较、边出栈。
代码样例:
public static int maxWidthRamp(int[] A) {
ArrayDeque<Integer> stack = new ArrayDeque<Integer>();
int maxLen = 0;
//选取递减元素入栈
for(int i = 0; i < A.length; i++) {
if(stack.isEmpty() || A[stack.peekLast()] > A[i]) {
stack.addLast(i);
}
}
//反向遍历集合,和单调栈中元素比比较。比较过后,已经是单调栈中此元素的最大值,本值出栈,不需要后续再比较
for(int j = A.length - 1; j >= 0; j--) {
while(!stack.isEmpty() && A[stack.peekLast()] <= A[j]) {
int top = stack.pollLast();
maxLen = Math.max(maxLen, j - top);
}
//栈空,返回,不需要再遍历
if(stack.isEmpty()) {
break;
}
}
return maxLen;
}