【算法】拓扑排序

一、算法理解

在图论中，拓扑排序（Topological Sorting）是一个 有向无环图（DAG, Directed Acyclic Graph）的 所有顶点的线性序列。且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次。
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

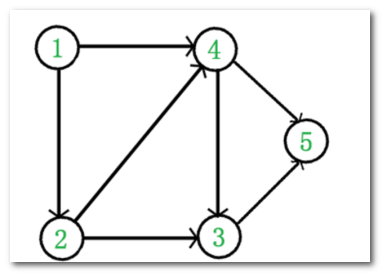
它是一个 DAG 图，那么如何写出它的拓扑排序呢？这里说一种比较常用的方法：

1. 从 DAG 图中选择一个 没有前驱（即入度为0） 的顶点并输出。
2. 从图中删除该顶点 和 所有以它为起点的 有向边。
   重复 1 和 2
   直到当前的 DAG 图为空 或 当前图中不存在 无前驱 的顶点为止。后一种情况说明有向图中必然存在环。
   

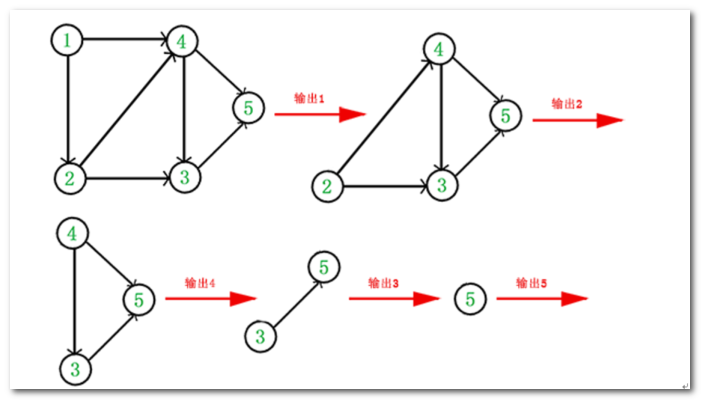
于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。通常，一个有向无环图可以有 一个或多个 拓扑排序序列。

二、适用场景

拓扑排序通常用来 排序 具有 依赖关系 的任务。比如：

如果用一个DAG图来表示一个工程，其中每个顶点表示工程中的一个任务，用有向边<A,B>表示在做任务 B 之前必须先完成任务 A。故在这个工程中，任意两个任务要么具有确定的先后关系，要么是没有关系，绝对不存在互相矛盾的关系（即环路）。

三、注意事项

1. 根据输入，建立有向图的 邻接 矩阵。需要记录，边、节点的入度。
   可以考虑如下结构表达：
   （1）方式一
   用Map<Integer, List>表示节点+边。 key：起始节点 List：本节点为始的边对应的终点。（1组起点+终点构成一条边）
   用Integer[]表示节点入度。 index：节点 Integer[index]：节点的入度
   （2）方式二
   用List[] Index：作为某个起始节点 List：起点关联的有向边的终止节点列表
   用Integer[]表示节点入度。 index：节点 Integer[index]：节点的入度
   （3）方式三
   用List<List<>>表示节点+边。 Index：作为某个起始节点 内List：起点关联的有向边的终止节点列表
   用Integer[]表示节点入度。 index：节点 Integer[index]：节点的入度
2. 宽度优BFS算法：
   • 入度为0的入栈
   • 出栈，找对应的入度点；删除线，对应的入度点 入度-1；入度变为0，继续入栈
3. 判断N个节点是都处理完毕； 完毕，无环；未完毕，有环。

四、算法样例参考

(1) 序列重建

给定一个原始序列（如[1,2,3]）和序列集（如：[1,2],[2,3]），验证原始序列是否可以 从 序列集 中唯一重建。
重建是指：
1）序列集中的序列 都是 原始序列的子序列
2）且原始序列是满足1）条件的最短序列

如：
（1）原始序列为[1,2,3]，序列集为[[1,2],[2,3]]，返回true
（2）原始序列为[1,2,3]，序列集为[1,2]，返回false。因为原始序列不满足2）条件。
（3）原始序列为[5,4,3,2,1,7]，序列集为[[3,2,1,7],[5,4,3,2]]，返回true

【解题思路】：
本地可以解析为需满足如下要求：

1. 任意两个数字的顺序 在 原始序列 和 序列集的序列中 必须一致。不能在一个序列中1在4后、另一个序列中1在4前。（拓扑图不能有环）
2. 序列集 中 并不能出现 原始序列 外的数字。
3. 原始序列 中 不能出现 序列集 外的数字。否则，原始序列就不是最小序列。

算法思路：

1. 把序列集转换成拓扑排序序列
2. 根据拓扑排序序列检索中所有元素总集合。要求：
   • 无环
   • 排序过程不能同时出现2个入度为0的节点，否则为唯一。（过程中A、B节点入度都为0，则存在AB、BA两种选择，序列不唯一）
3. 拓扑排序集合 和 原始集合相同。

那么我们可以用了一个一维数组pos来记录org中每个数字对应的位置，然后用一个flags数字来标记当前数字和其前面一个数字是否和org中的顺序一致，用cnt来标记还需要验证顺序的数字的个数，初始化cnt为n-1，因为n个数字只需要验证n-1对顺序即可，然后我们先遍历一遍org，将每个数字的位置信息存入pos中，然后再遍历子序列中的每一个数字，还是要先判断数字是否越界，然后我们取出当前数字cur，和其前一位置上的数字pre，如果在org中，pre在cur之后，那么直接返回false。否则我们看如果cur的顺序没被验证过，而且pre是在cur的前一个，那么标记cur已验证，且cnt自减1，最后如果cnt为0了，说明所有顺序被成功验证了，参见代码如下：

源码参考（Java）

// run是入口为例
public class RebuildArray {
    class Node {
        // 记录节点的出度
        ArrayList<Integer> outLine = new ArrayList<>();
        // 记录节点的入度
        Integer inCount = 0;
    }
    // 记录拓扑排序节点树
    HashMap<Integer, Node> topoTree;

    public void run() {
        Integer[] orgArray = new Integer[]{1,2,3};
        Integer[][] arrayDictory = new Integer[][]{{1,2},{2,3}};
        System.out.println(TopoSortCheck(orgArray, arrayDictory));
    }

    public boolean TopoSortCheck(Integer[] org, Integer[][] array) {
        topoTree = new HashMap<Integer, Node>();

        // 序列集转换成Topo排序树
        for (int i = 0; i < array.length; i++) {
            addArrayToTopoTree(array[i]);
        }

        // 拓扑排序树转换序列
        ArrayList<Integer> tmpList = new ArrayList<>();
        if (!getArrayFromTopoTree(dirList)) {
            return false;
        }

        // 比较托树序列和原始序列是否一致
        return tmpList.equals(new ArrayList<>(Arrays.asList(org)));
    }

    public void addArrayToTopoTree(Integer[] array) {
        for (int i=0; i<array.length; i++) {
            // 创建节点
            if(!topoTree.containsKey(array[i])) {
                topoTree.put(array[i], new Node());
            }

            // 记录序列集中前一节点和后一节点关系
            if (i >= 1) {
                Node preNode = topoTree.get(array[i-1]);
                Node curNode = topoTree.get(array[i]);
                if(!preNode.outLine.contains((Integer)array[i])) {
                    preNode.outLine.add(array[i]);
                    curNode.inCount++;
                }
            }
        }

        return;
    }

    public boolean getArrayFromTopoTree(ArrayList<Integer> nodeList) {
        // 记录入度是0的节点
        Integer rootNode = -1;
        // 记录入度是0的节点数量
        Integer count = 0;

        while (!topoTree.isEmpty()) {
            // 遍历剩余节点集中入度为0的节点
            Set<Integer> keset = topoTree.keySet();
            for (Integer key: keset) {
                Node node = topoTree.get(key);
                if (node.inCount == 0) {
                    rootNode = key;
                    count++;
                    // 存在多个入度为0节点，序列不唯一
                    if (count > 1) {
                        return false;
                    }
                }
            }

            // 找不到入度是0的节点，则出现循环
            if (rootNode == -1) {
                return false;
            } else {
                // 减少下一节点入度
                for (Integer nextNodekey: topoTree.get(rootNode).outLine) {
                    topoTree.get(nextNodekey).inCount--;
                }
                // 当前节点放入队列
                nodeList.add(rootNode);
                // 删除当前节点
                topoTree.remove(rootNode);
            }

            // 初始数据
            rootNode = -1;
            count = 0;
        }

        return true;
    }
}