一个矩阵就相当于一个基。
例如:
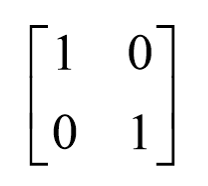
这个矩阵是我们常见的基，是笛卡尔坐标系的基。
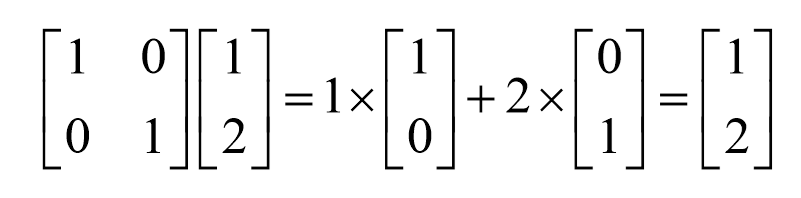
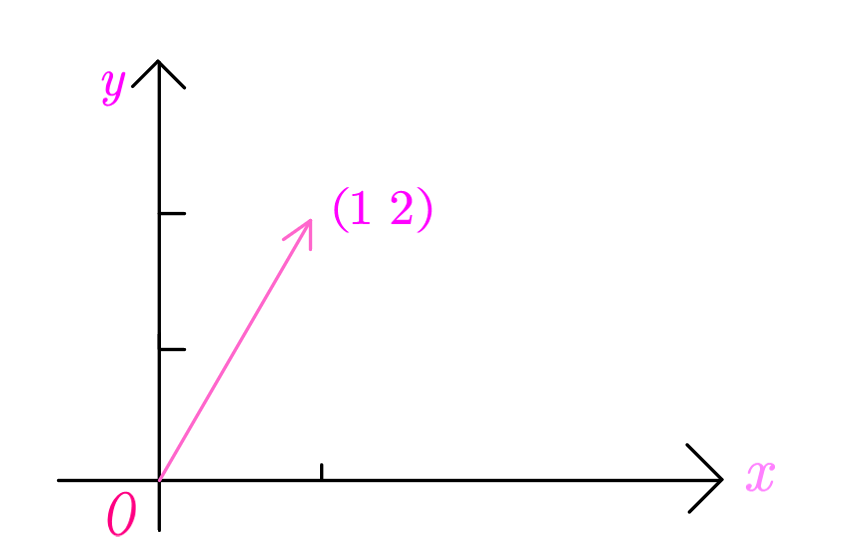
在这个基的作用下，向量被映射后，还是它本身。相当于是1倍的
向量加上2倍的
向量。
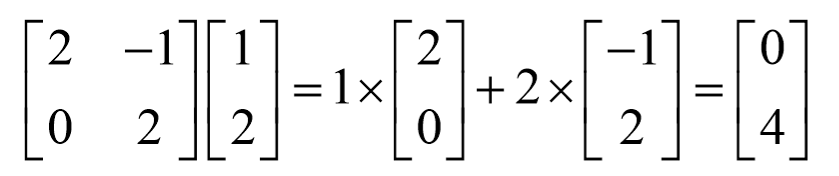
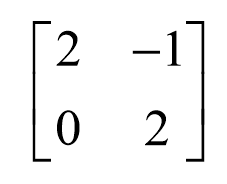这也是一个基。
在这个基的作用（映射）下，向量
被映射成了
，这个结果仍然是相当于1倍的第一个基+2倍的第二个基的结果。
一步一步的来：
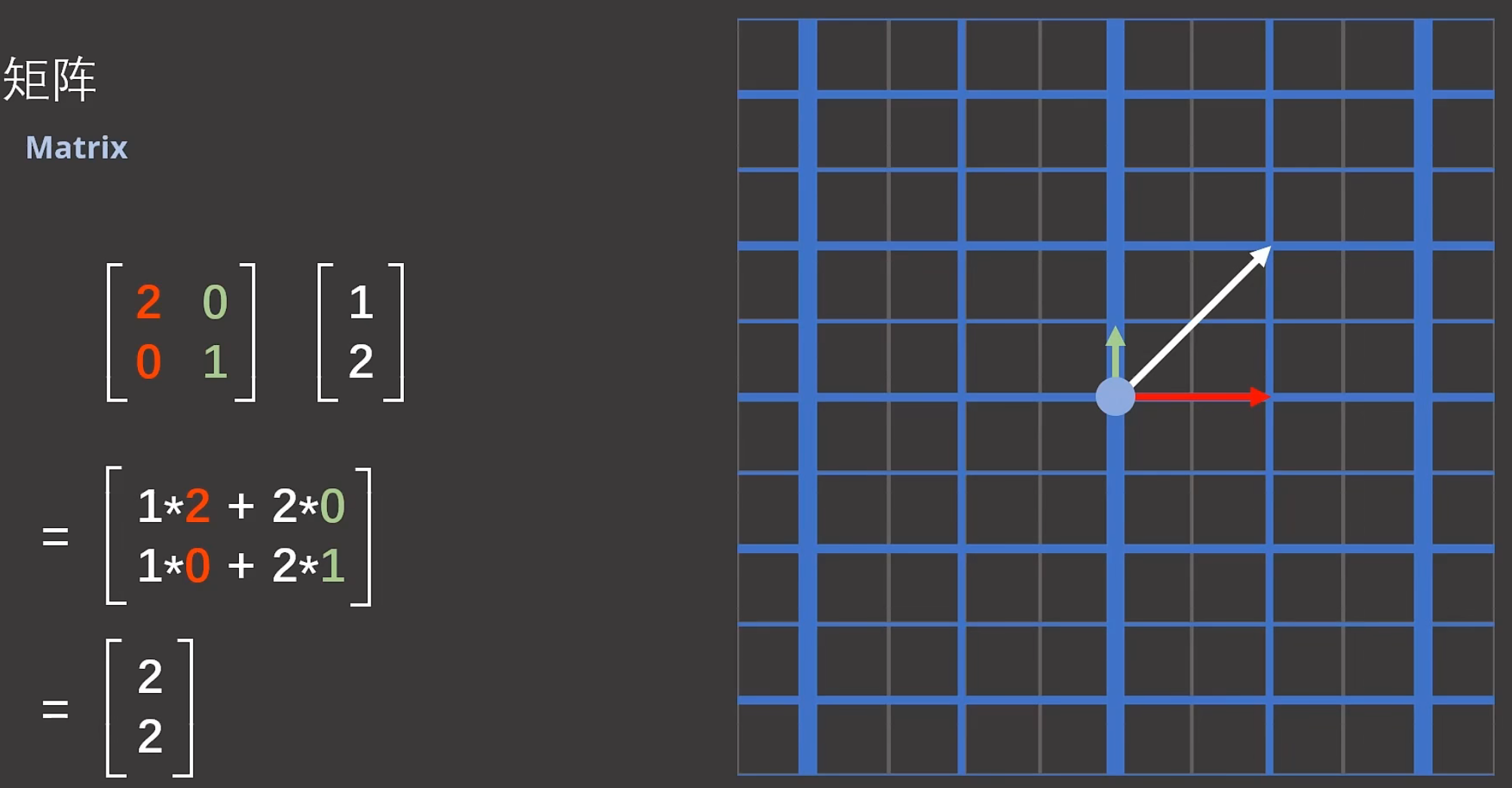
第1步：首先把第1个基变成：
即把在x轴方向上伸长为原来的2倍。
第2步：把第2个基变成：
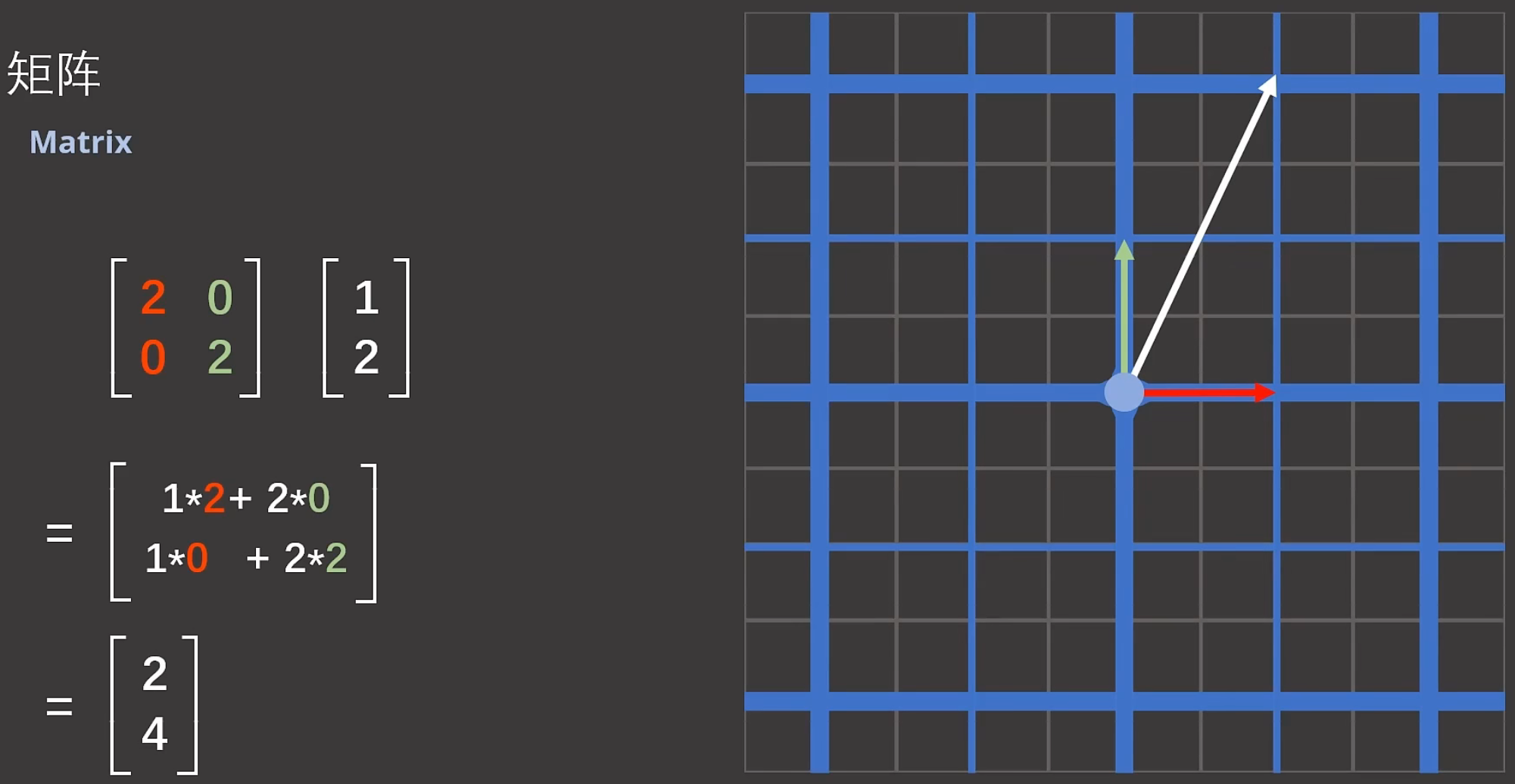
第3步：把第2个基变成：
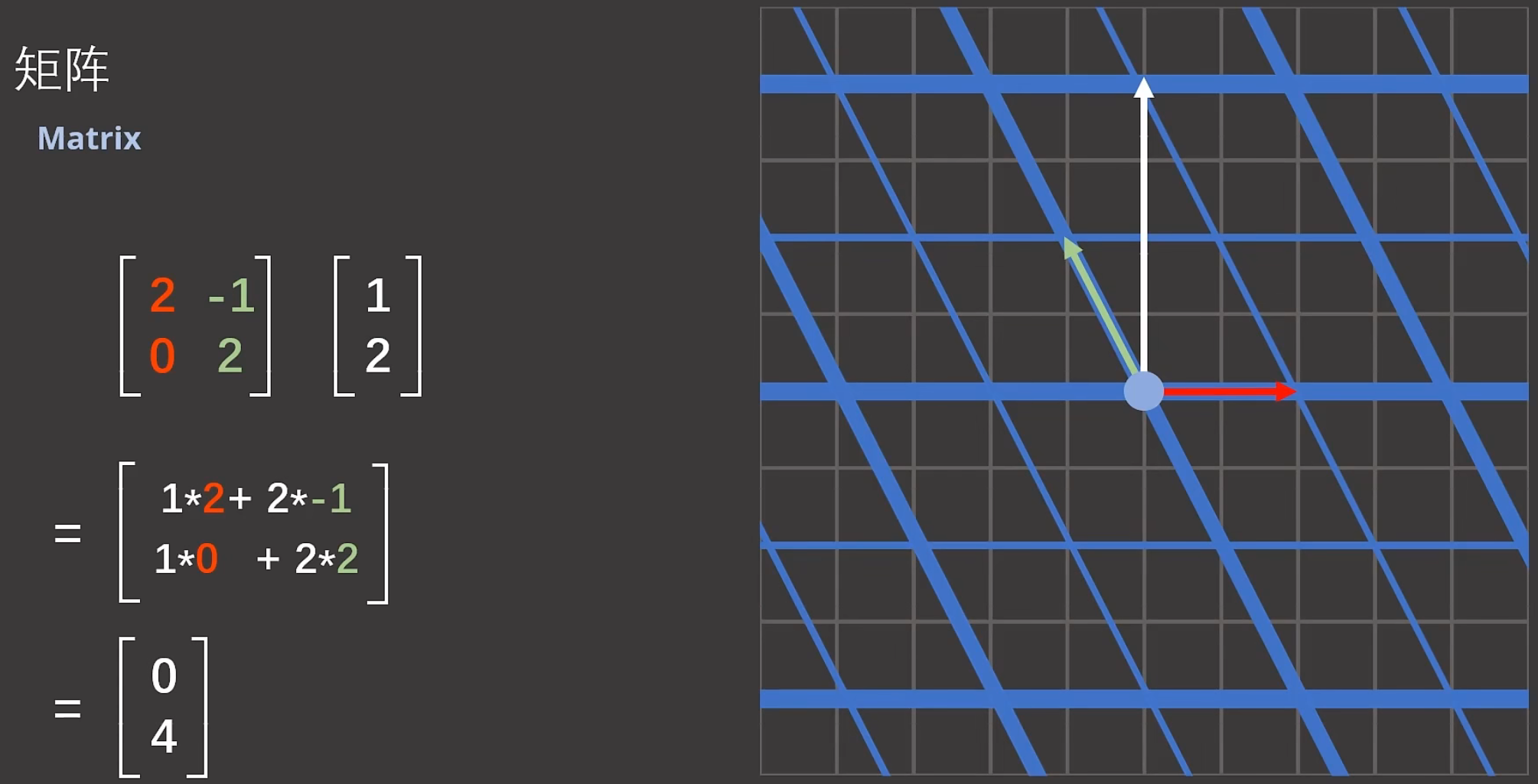
白色向量在奇怪的坐标系（新基准构成的坐标系）里面，在横轴上还是一个单位，在纵轴上还是2个单位，相当于在新基准中，还是向量。只不过回到原始的坐标系中，就是向量.
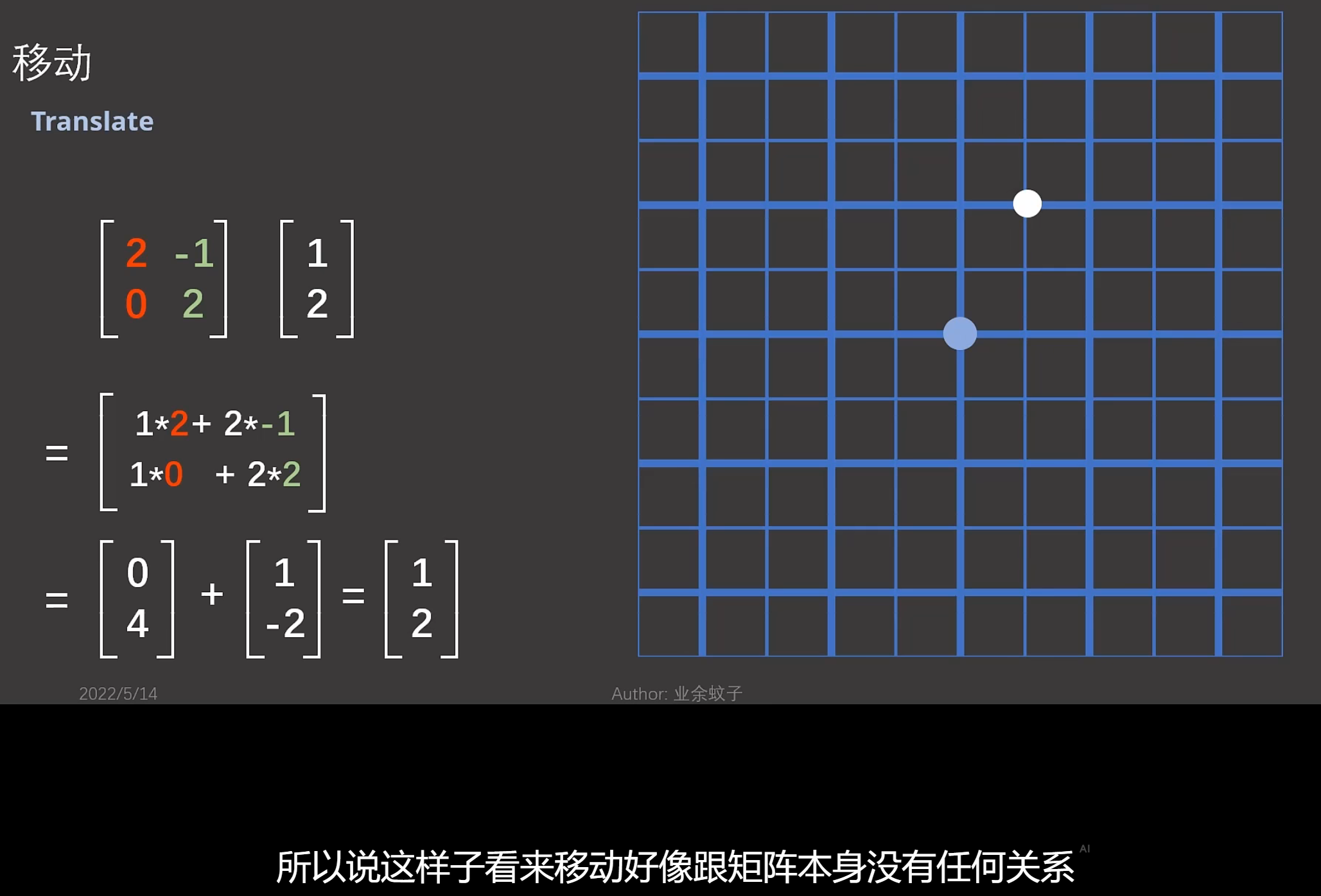
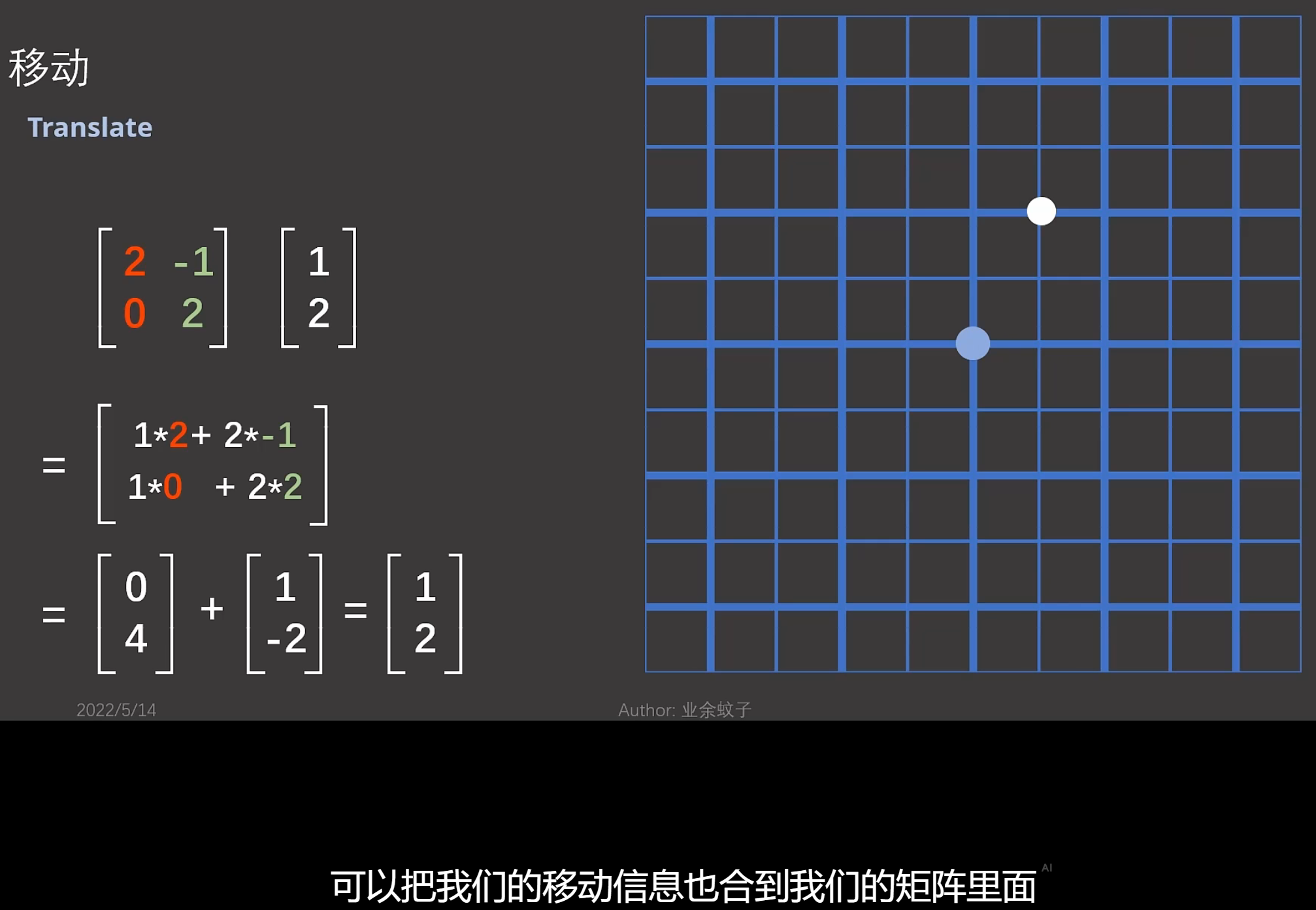
如果是行向量和矩阵相乘，那么，矩阵的每个行向量组成新坐标系的基。如下：
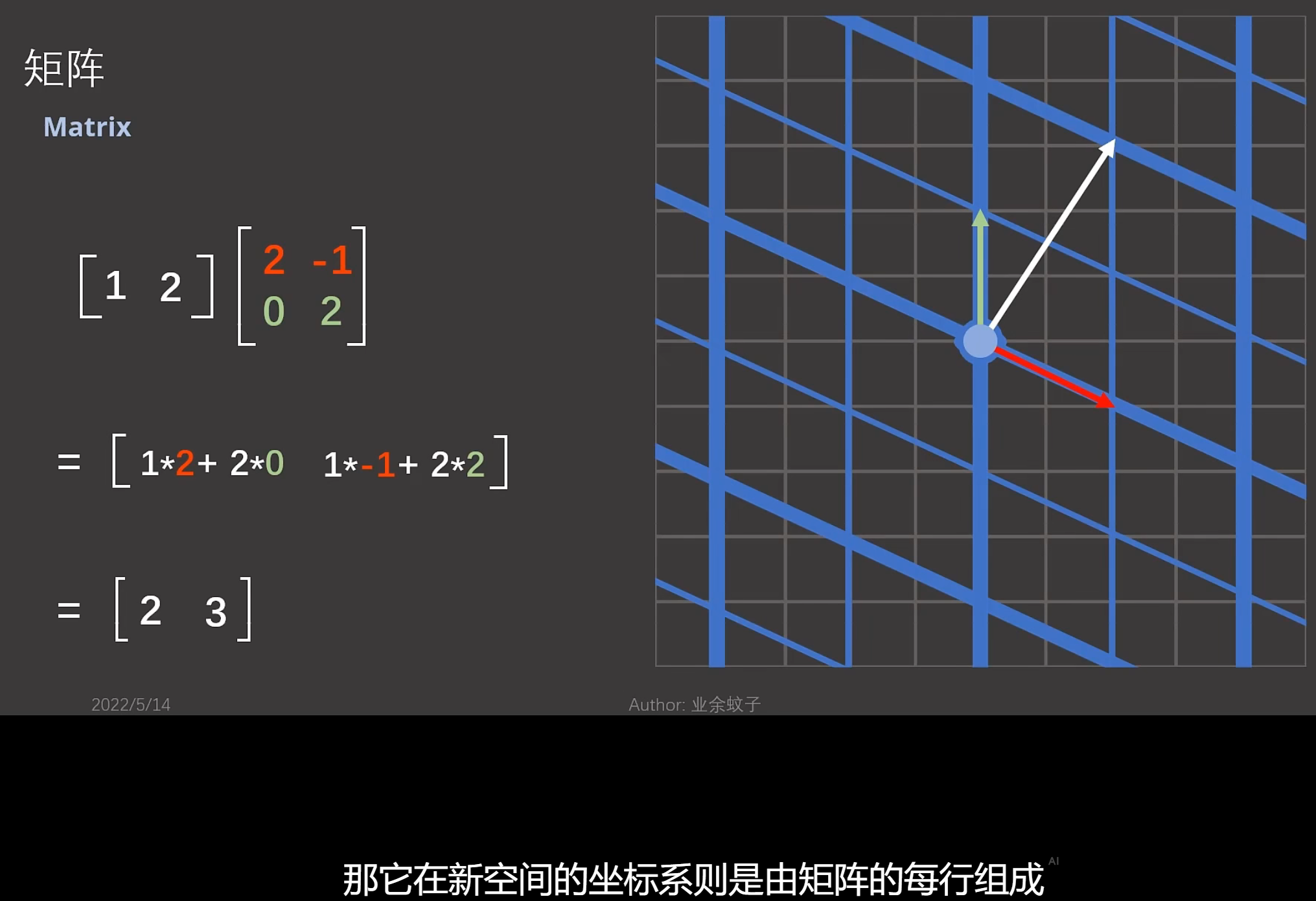
但是，一般是考虑矩阵和列向量相乘。
注解：
1.先向p向量移动x个单位，再向q向量移动y个单位。
2.假如p、q向量分别是标准笛卡尔坐标系中的x轴和y轴，那么结果就是坐标或者向量
3.p向量和q向量，相当于是标准笛卡尔坐标系中的x轴和y轴。
注解：
1.p向量和q向量，还有另外的名字，叫做基向量。
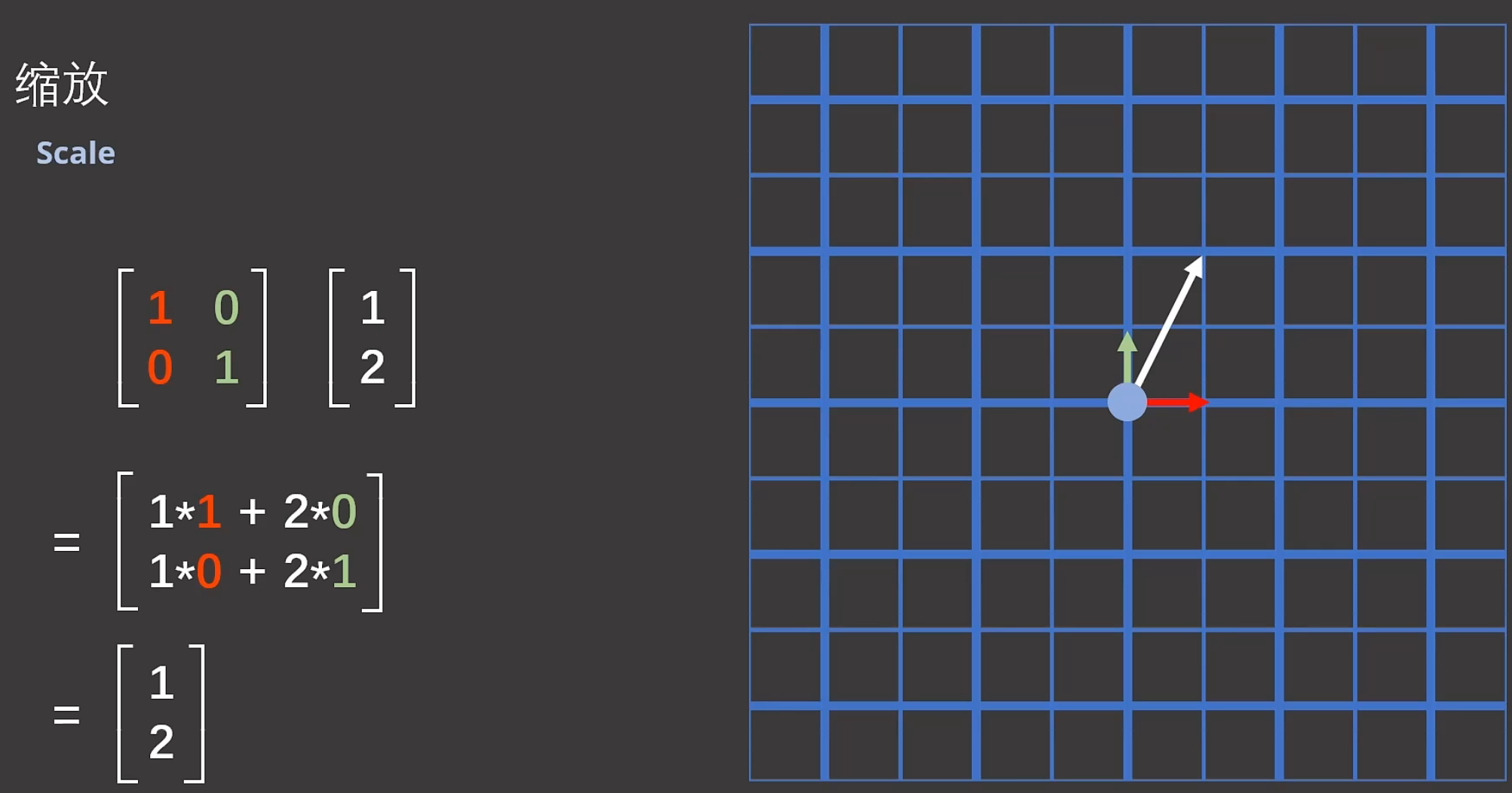
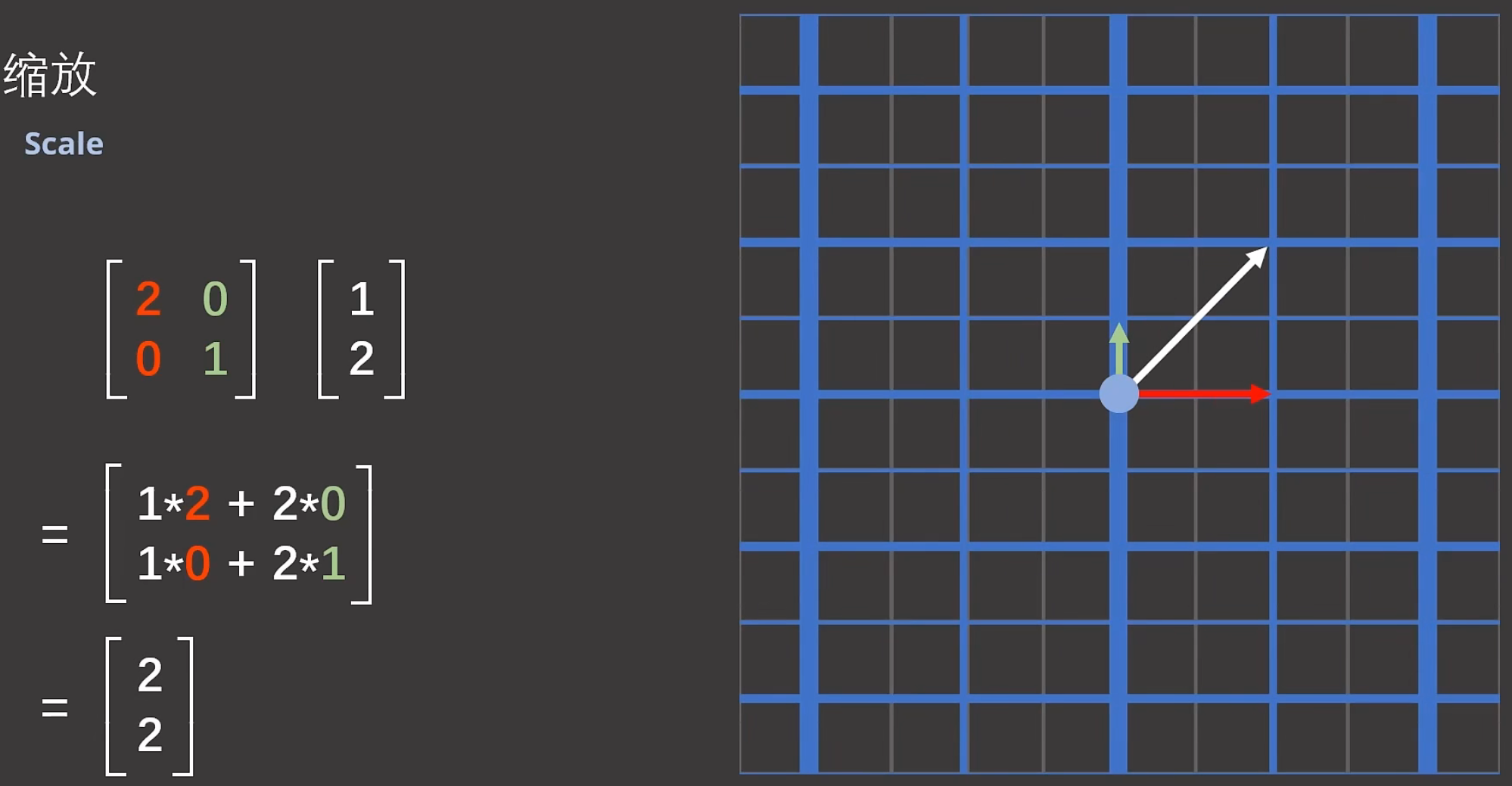
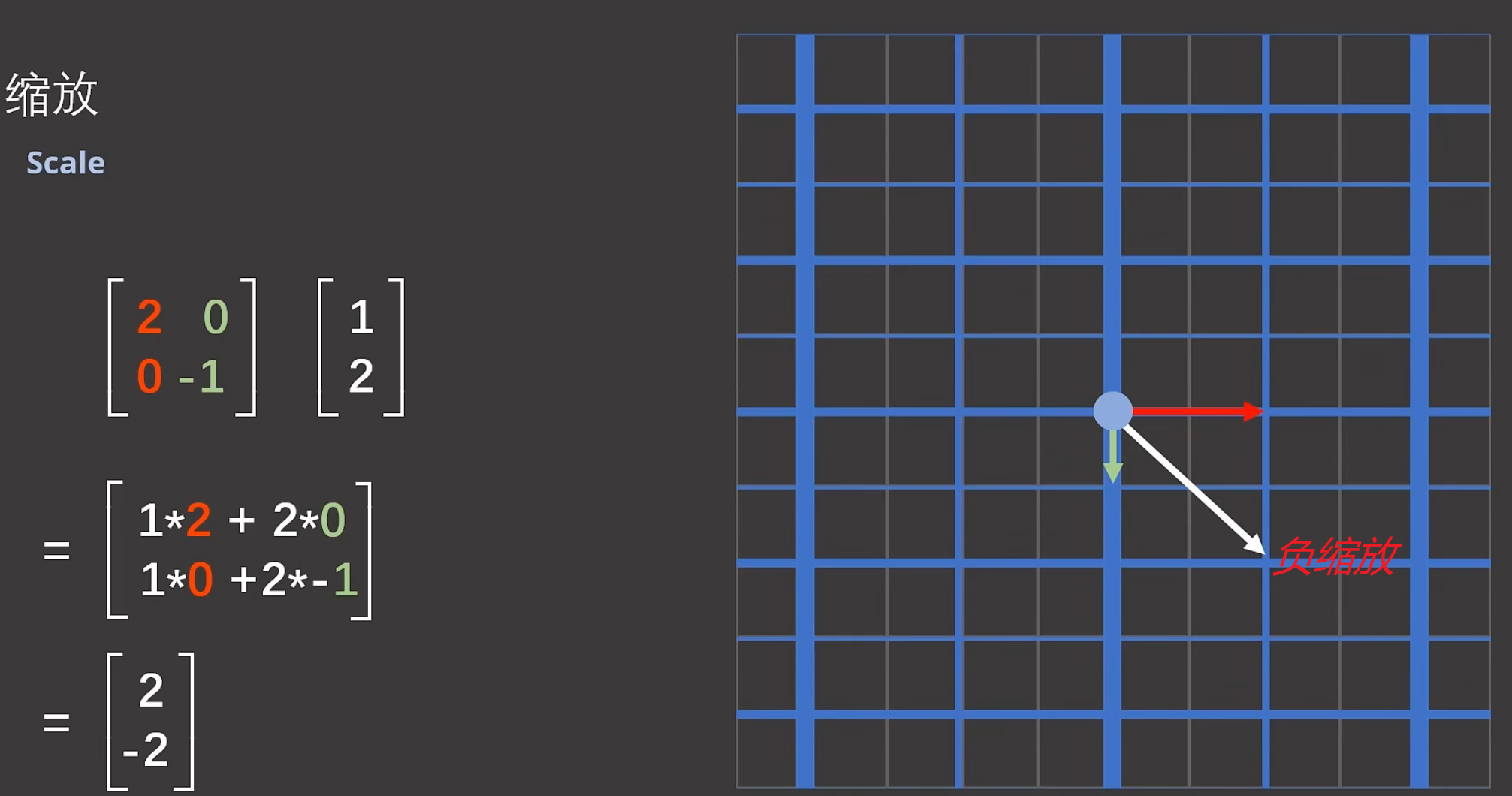
注解：
1.缩放其实最简单，因为只需要修改矩阵对角线上的元素就行了。
旋转：
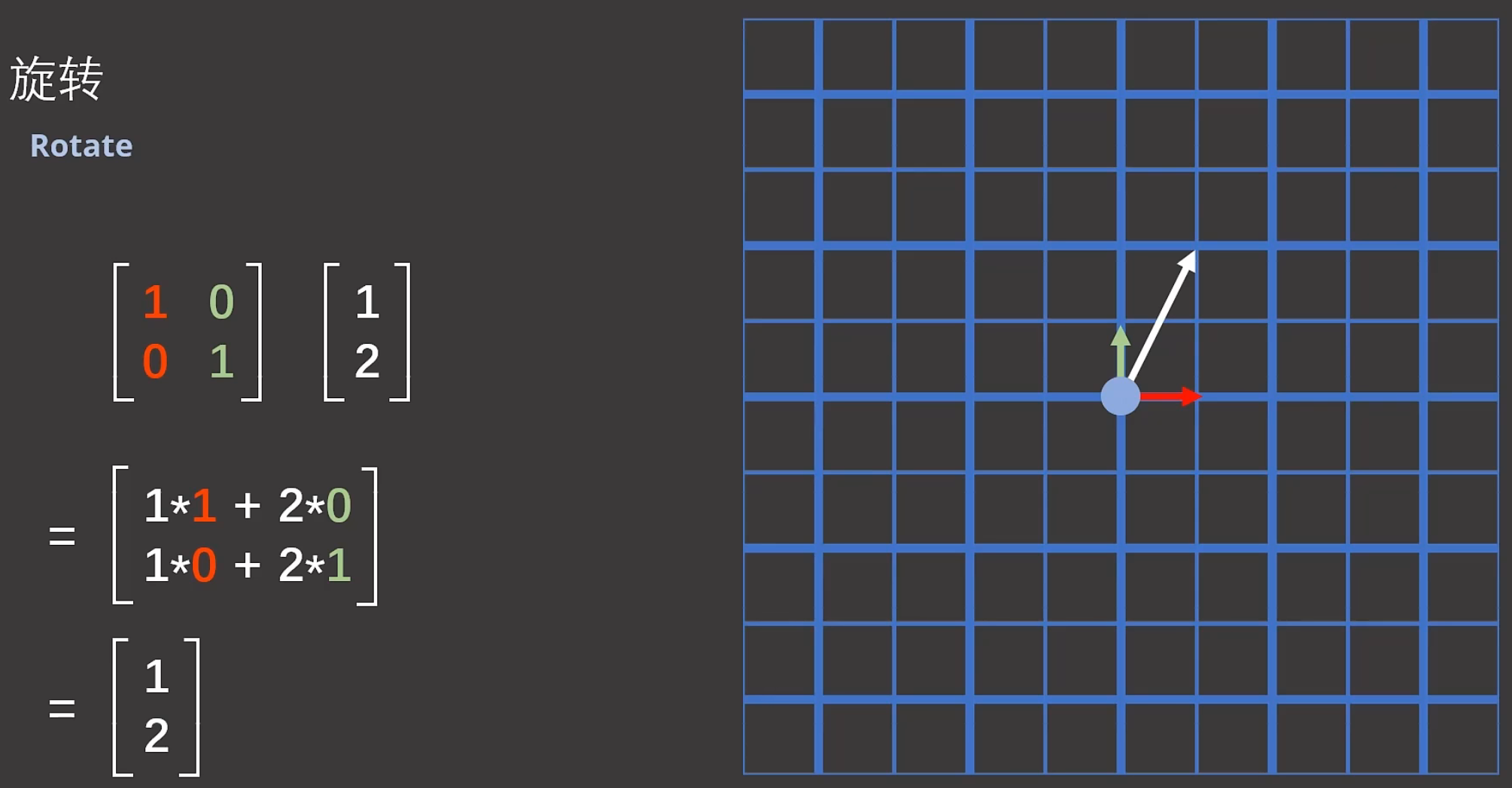
坐标系逆时针旋转90°后，新的基向量是
和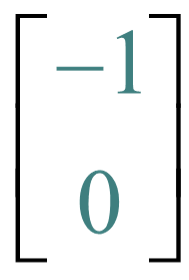
：
注解：
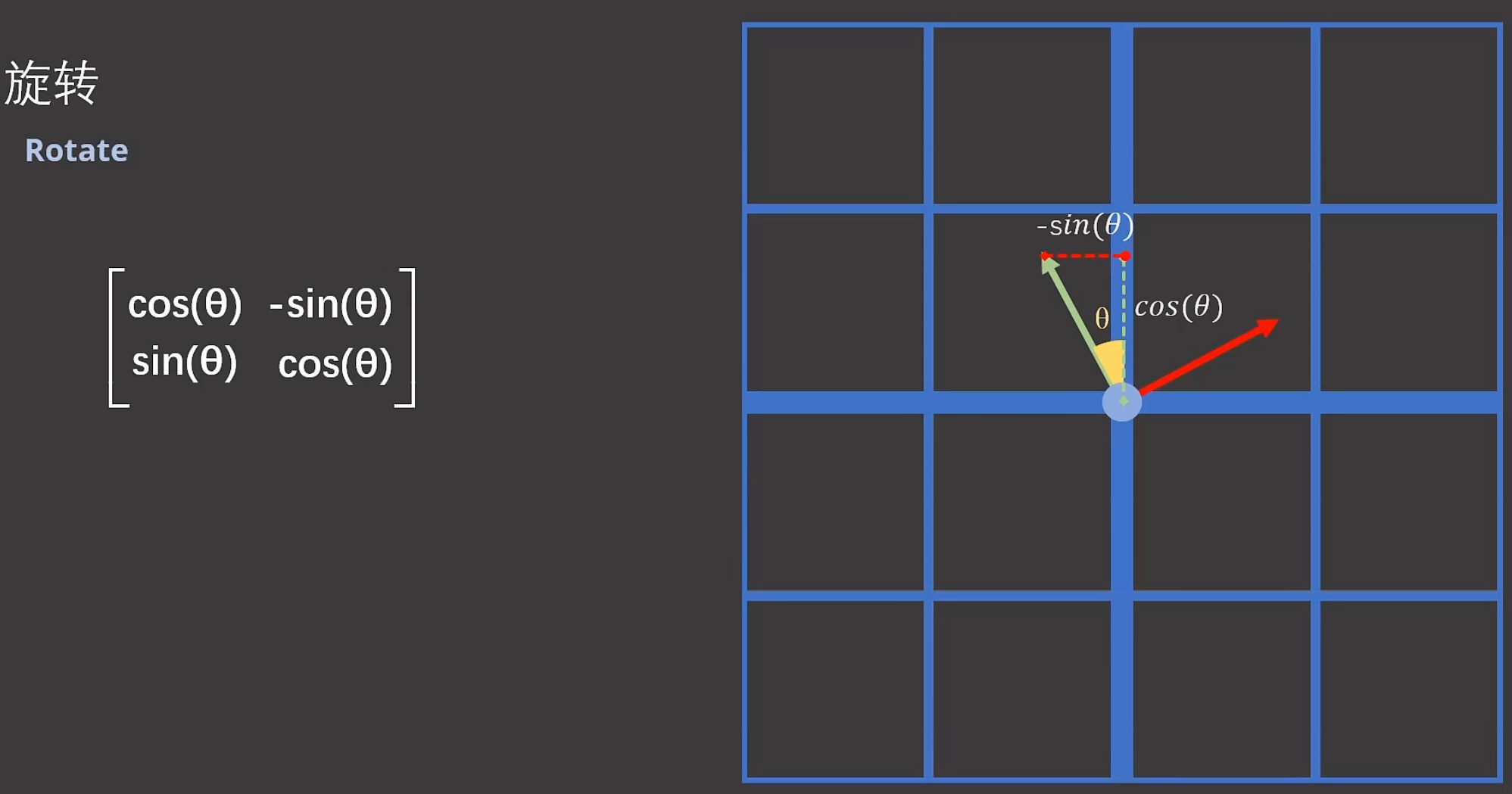
1.这其实是个特定方向的旋转，但是我们平时做的旋转很多情况下是有一定度数的旋转。这就需要知道一般的旋转公式。
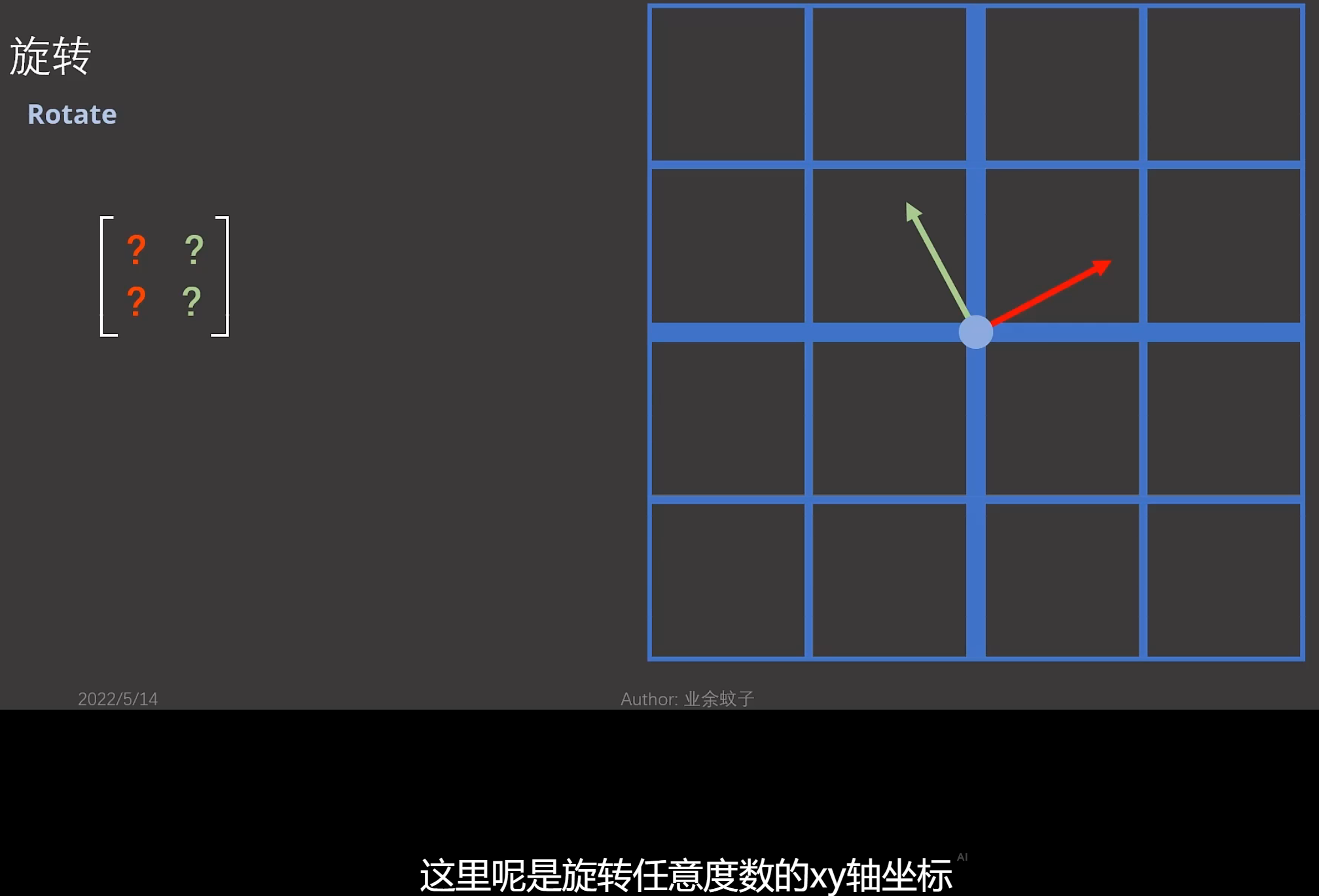
注解：
1.只要知道新的基的坐标就行了，即新的基在原始坐标系的中的坐标(x轴和y轴上的值)，就知道旋转矩阵的样子了。
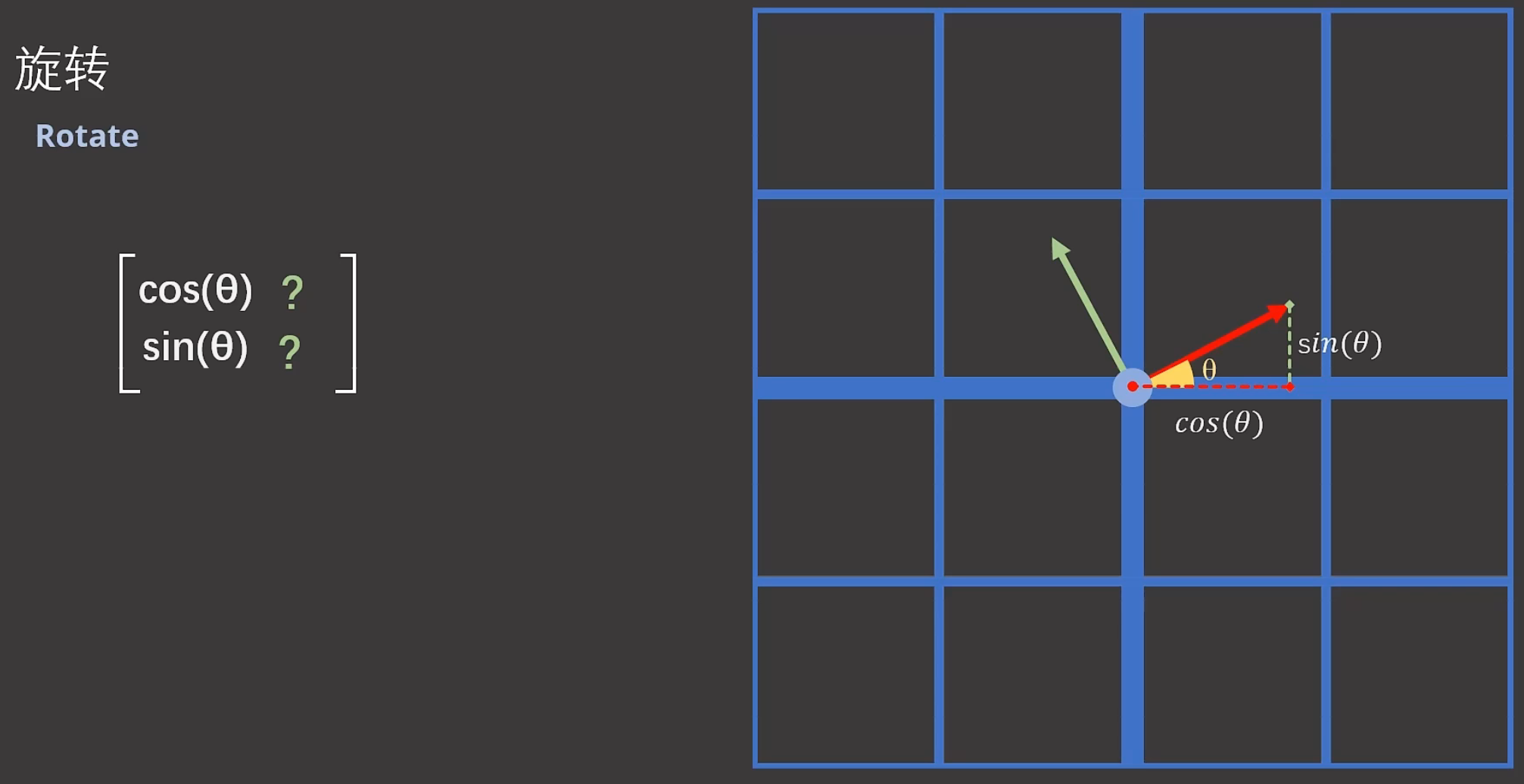
注解：
1.旋转的度数θ是已知的，因为是给定的度数。
2.新的第1个基向量是一个单位向量。
