数据科学【系列1】|统计入门|正态分布和概率密度函数(上)_哔哩哔哩_bilibili
很多假设检验有一定的前提条件,要求数据有一定的正态性,中心极限定理充当了这一桥梁。
连续型随机变量的一个很重要的分布就是正态分布。
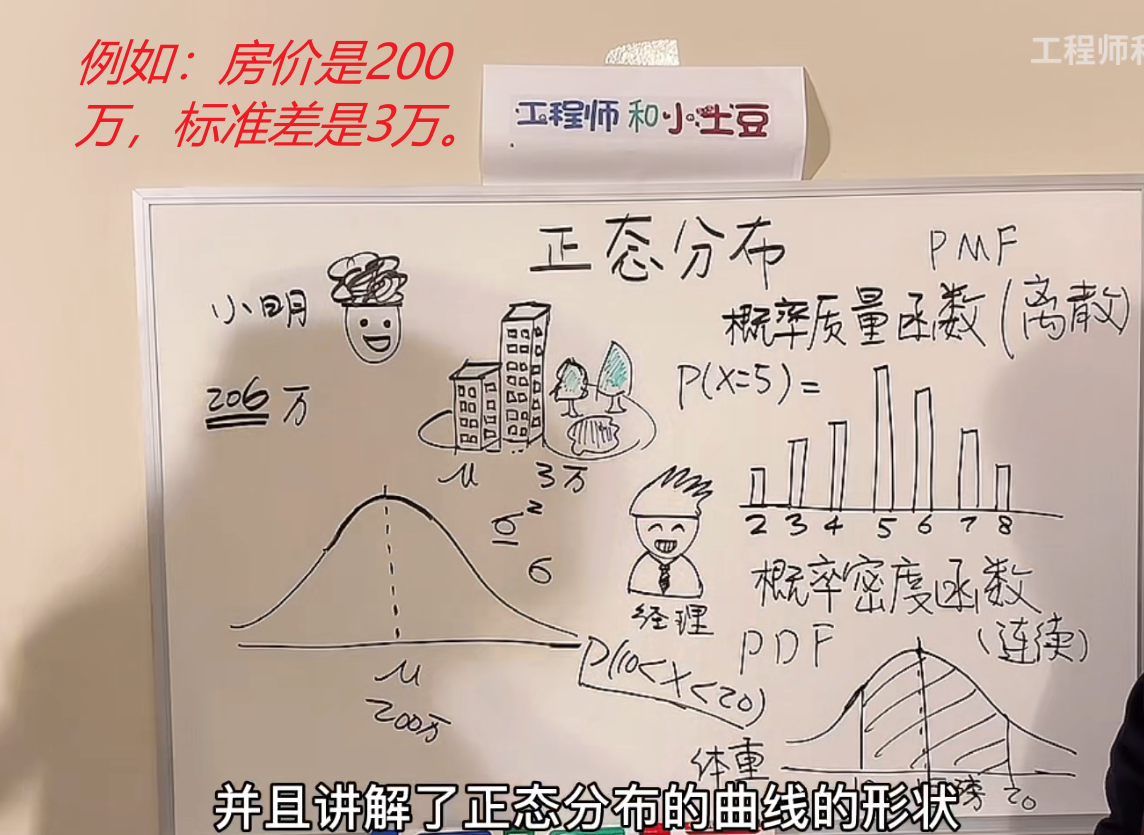
例子:小明买楼盘或者别墅,只有206万块钱。所以,他要利用概率和统计的知识估计自己的钱够不够。判断下房价小于206万的概率,从而知道一下自己的钱够不够买别墅。
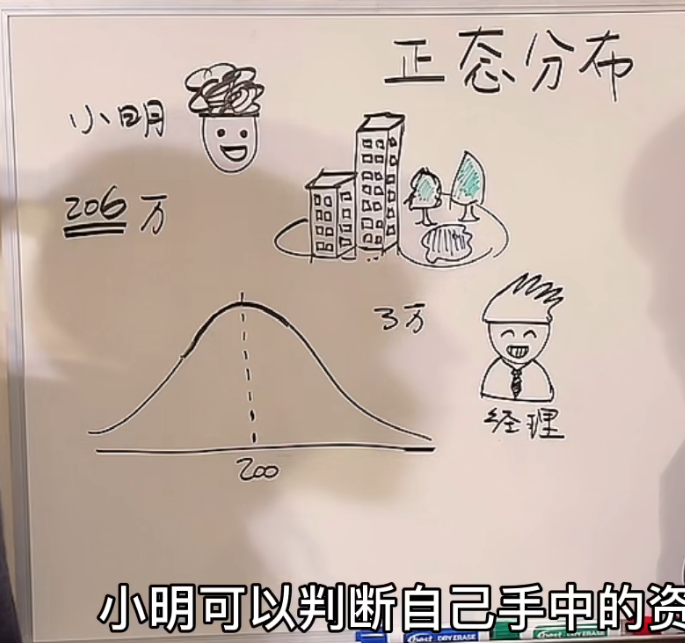
假设楼市的价格的分布服从于正态分布。
引入两个概念:
描述离散型随机变量的概率分布:概率质量函数。
描述连续型随机变量的概率分布:概率密度函数。
离散型随机变量举例:
猫妈妈生小猫,每一窝生的小猫的数量是个随机数。
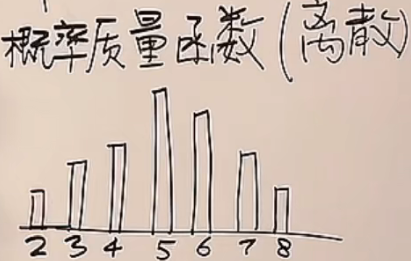
2、3、4、5、6、7、8是生的小猫的数量,柱状图是对应的概率。

注解:
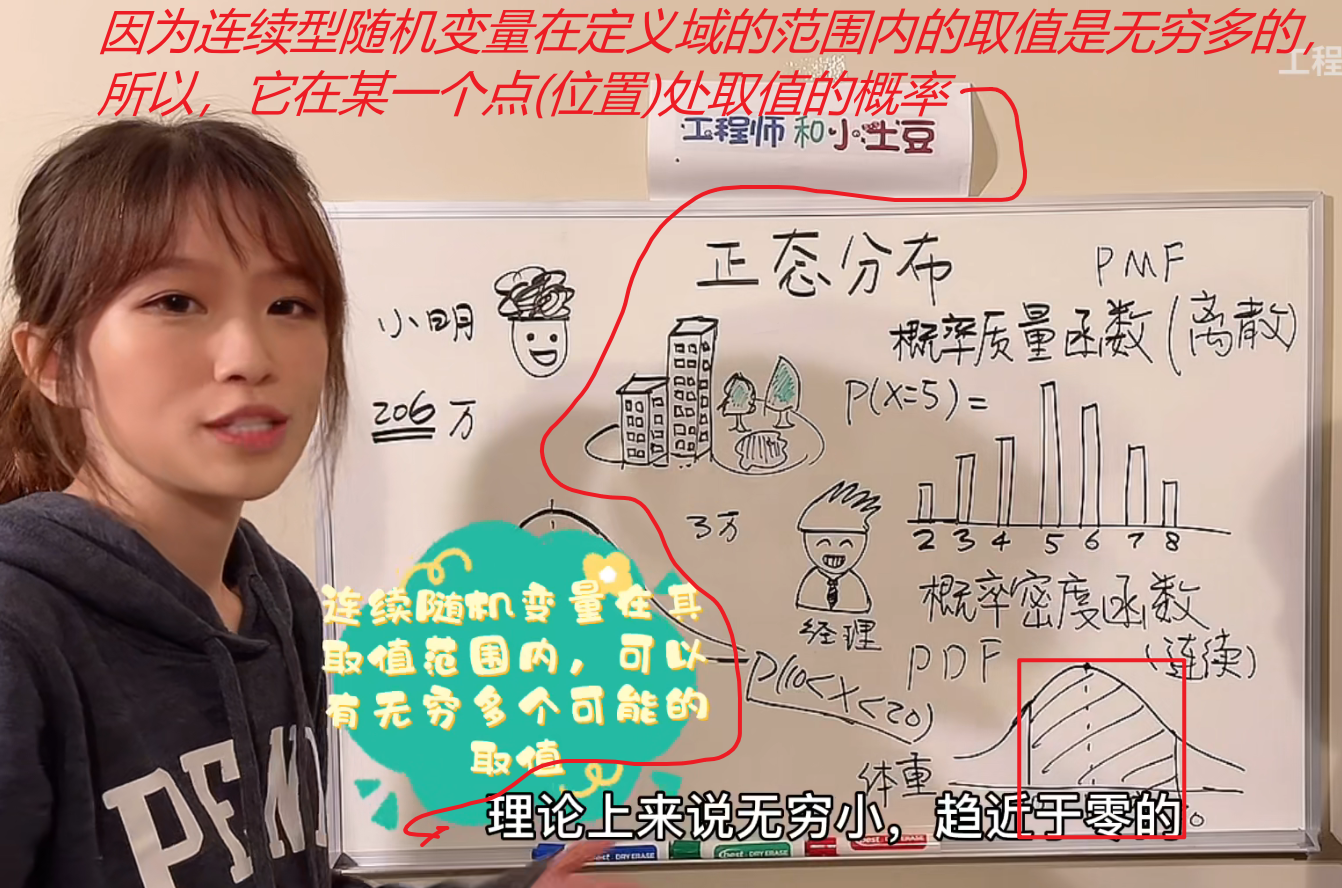
1.离散型随机变量,可以求得它取某一个具体值的时候,它的概率是多少。
注解:
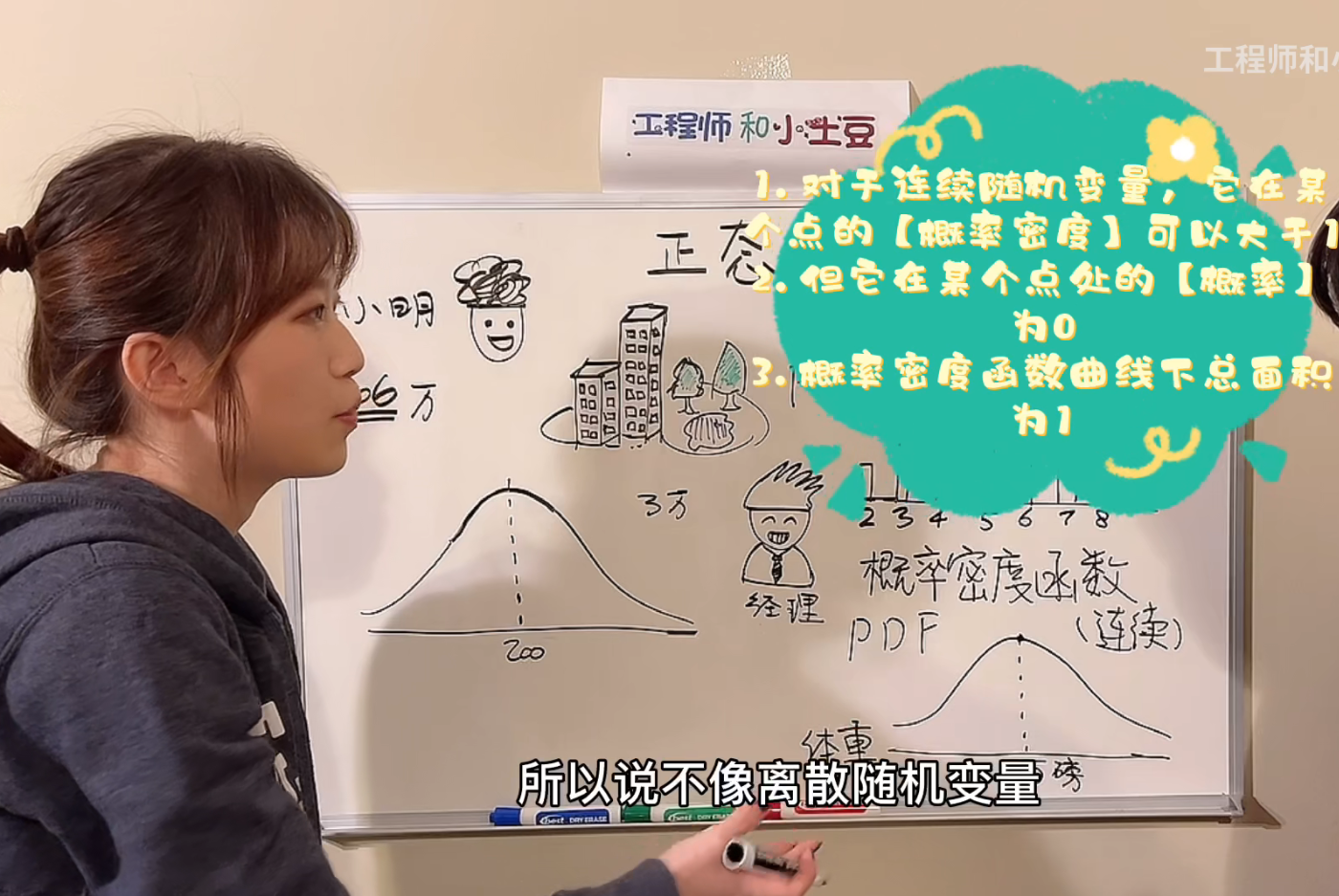
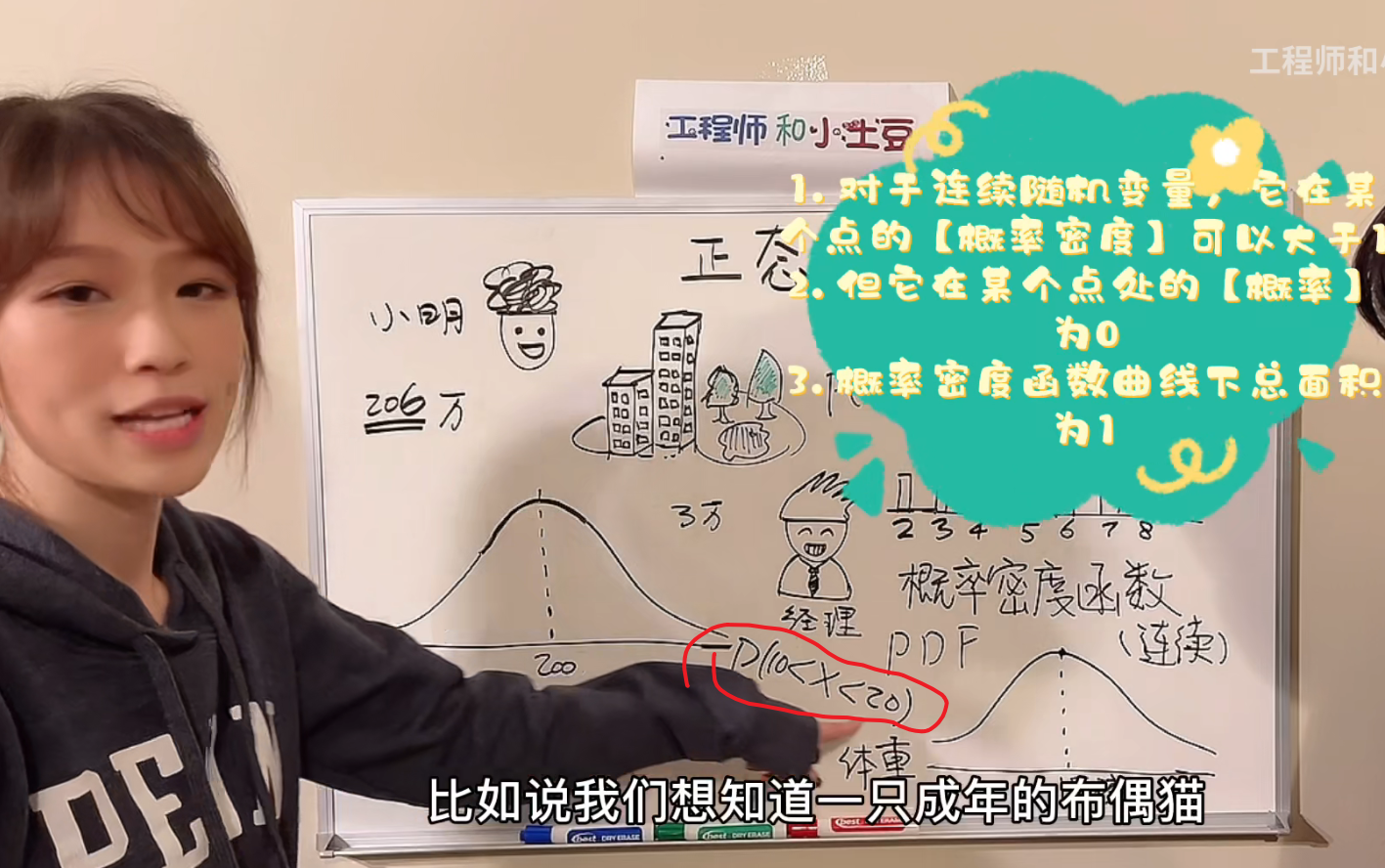
1.连续型随机变量的概率密度函数的图像,它的纵坐标是变量取某一个具体值的概率密度,而不是概率。
2.对于连续型随机变量,一般会求某个随机变量在某一个取值范围内,它的概率是多少。
注解:
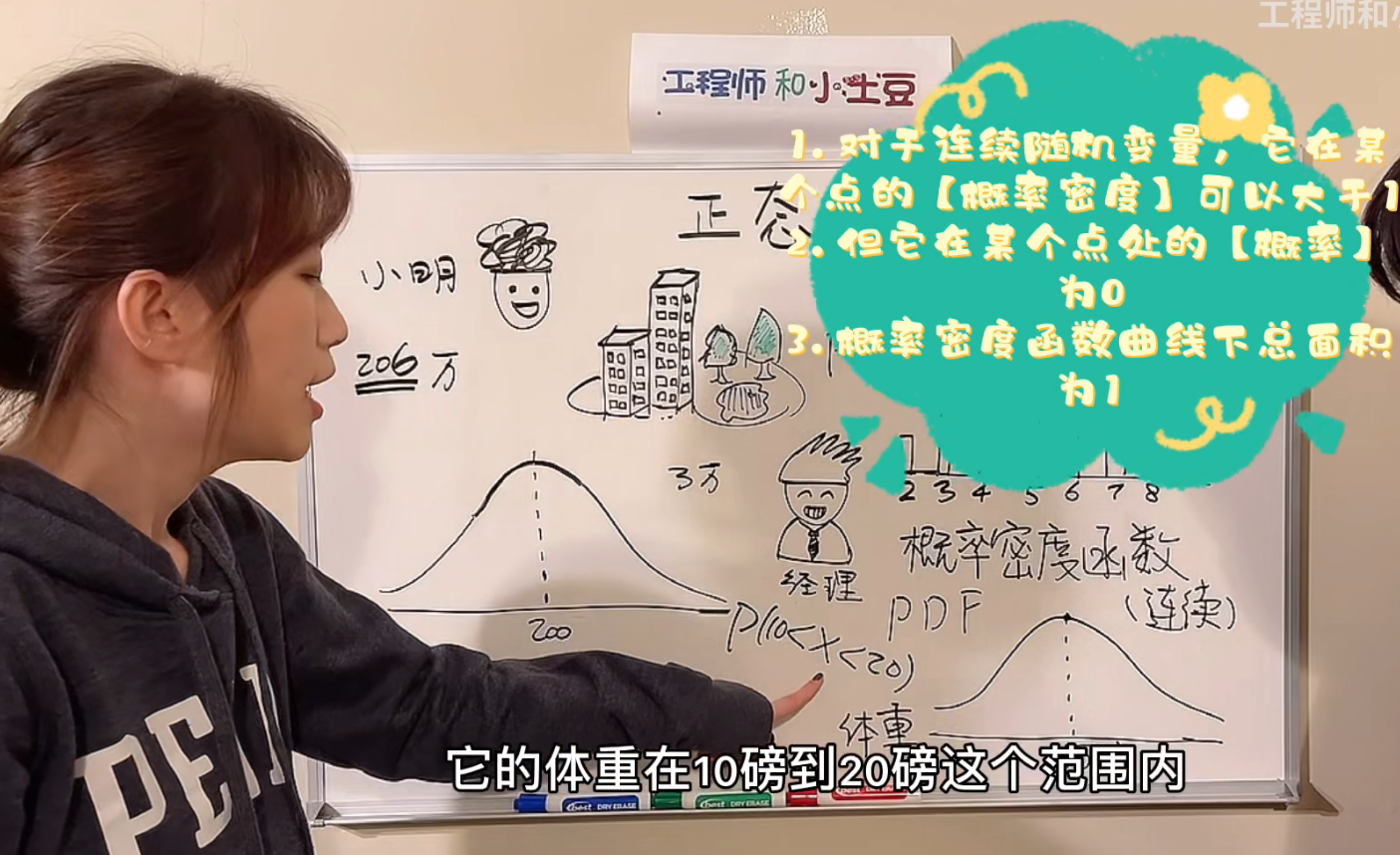
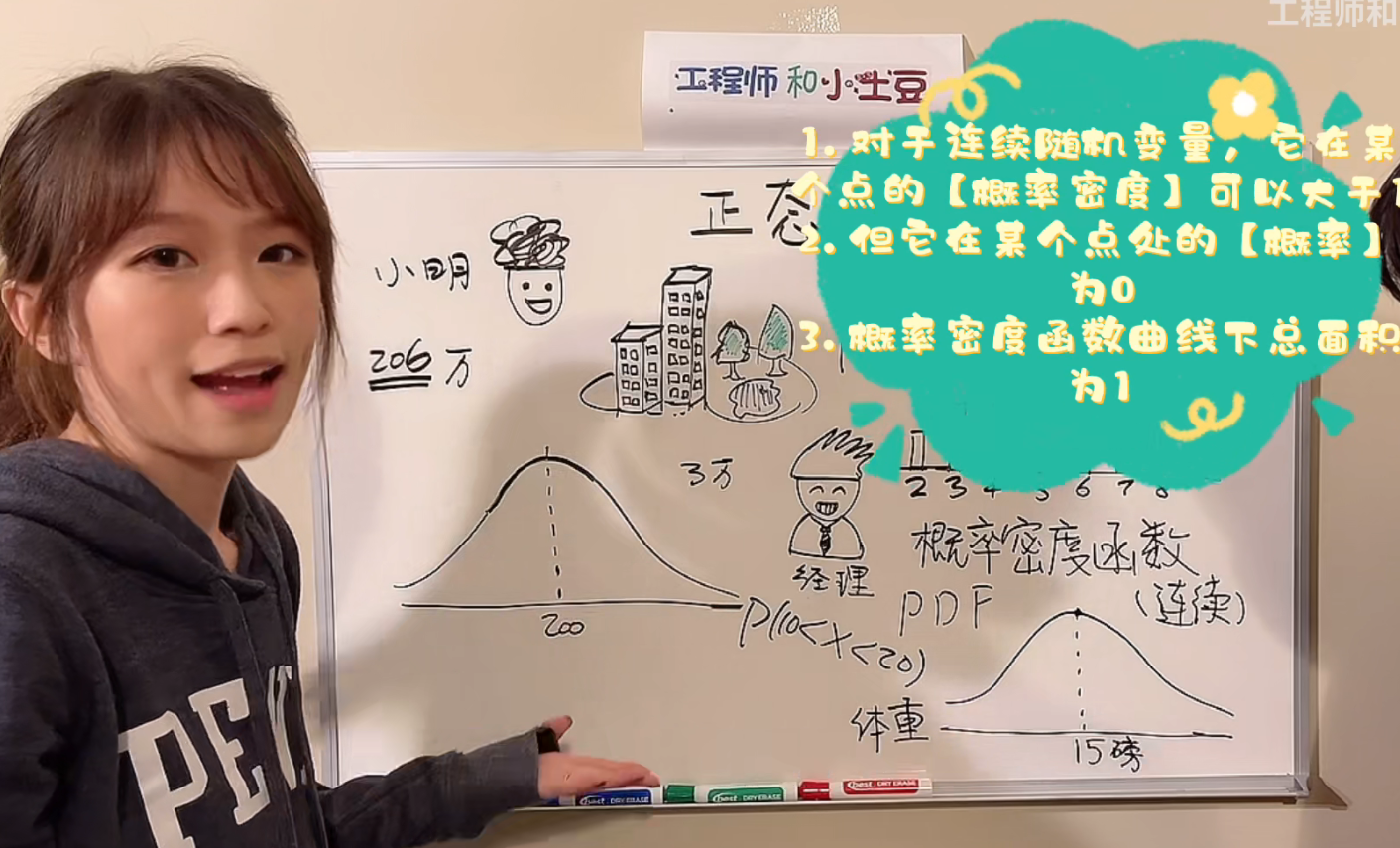
1.体重在10到20磅的这个范围内的概率是多大?
答:是对应的曲线下面阴影部分的面积。
注解:
1.连续型随机变量取某个值的概率是0的另一个解释是:连续型随机变量取某个值的概率对应图像上的一条线,而一条线是没有面积的,所以,取某个值的概率是0.

注解:
1.方差/标准差描述了一些数据相对于它们的均值而言,是多么的分散。