神经网络与深度学习(更新至第6讲 循环神经网络)_哔哩哔哩_bilibili
注解:
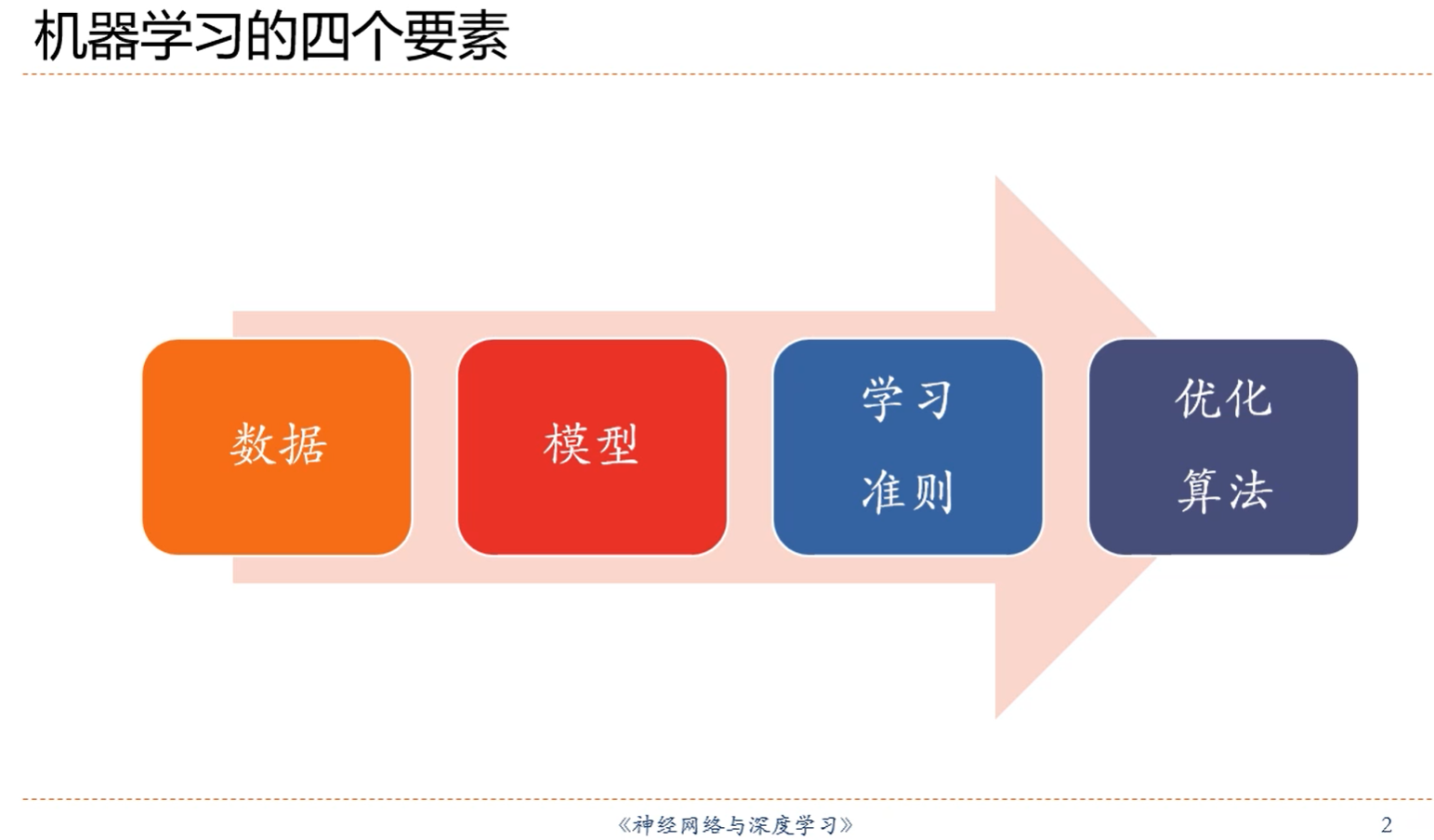
1.在假定的空间中建立一个最优的模型,利用这个模型建立x和y之间的关系。
2.需要有一个准则来判断学习到的模型是好是坏。

注解:
1.左边是线性模型,右边是非线性模型。

注解:
1.函数的预测值f(x,θ*)与真实值y的差异应该是尽可能的小,很小很小,小到一个很小的数。
2.这个损失函数是在一个单点上的平方,对于整个模型的话,是希望在所有的样本点上平方的累加和最小。
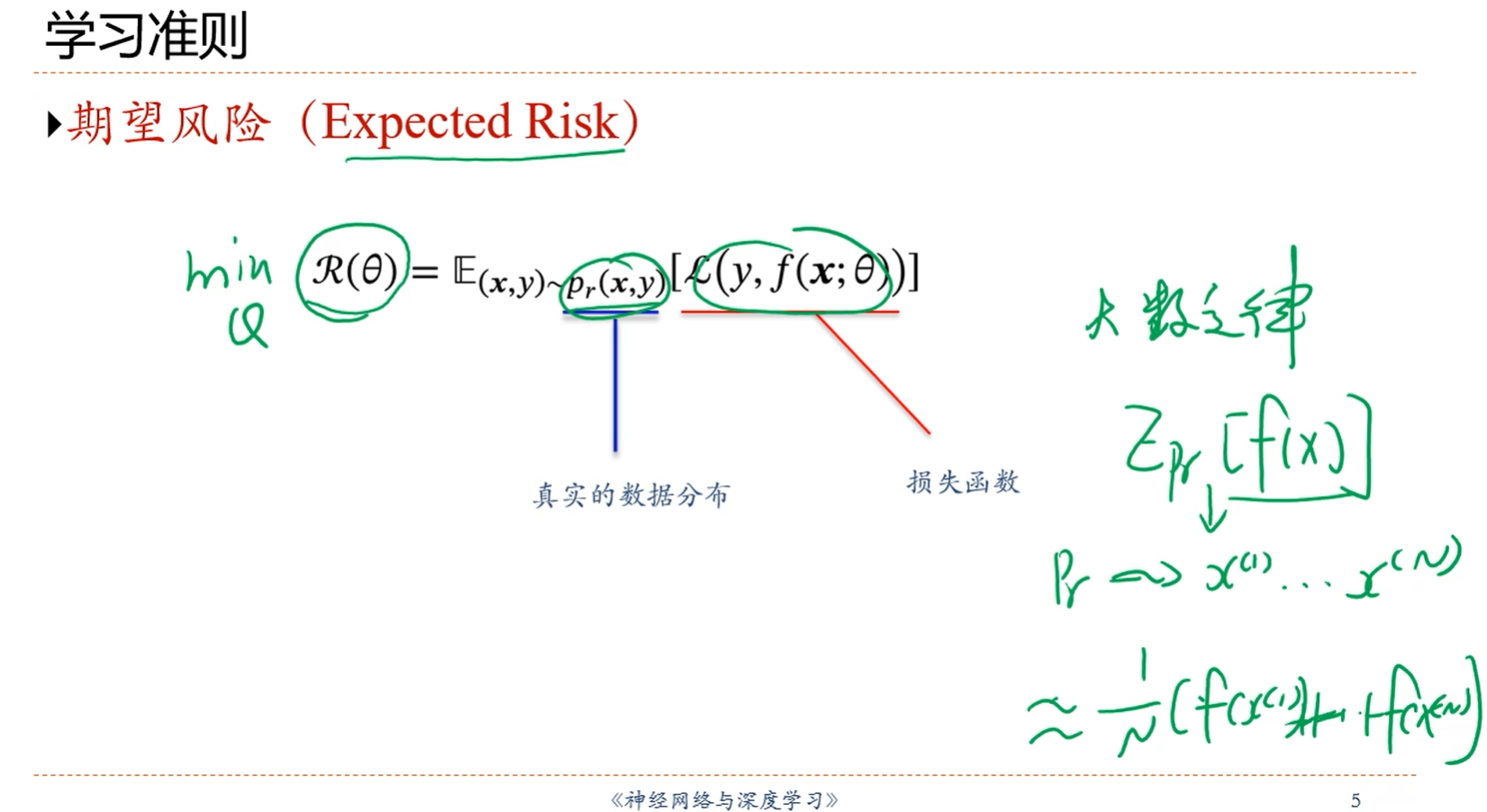
注解:
1.真实的损失函数的期望不知道,但是可以通过采集很多很多的样本去近似计算这个期望值。

注解:
1.根据大数定律,当N趋近于无穷大的时候,经验风险就逼近于期望风险。
2.经验风险,就是对采样到的有限个样本点上的损失取平均。
3.经验风险中的字母D代表:Distribution.

注解:
1.凸函数等价于:二阶导>0(网友:二阶导>0等价于凹函数?)。
2.凸函数极值点是唯一的,所以一阶导求出来的x值,即极值点一定是全局最优的。
3.在机器学习中,如何使用一个比较高级的算法解决非凸优化也是一个重要的研究的问题。

注解:
1.梯度下降法可以类比于适一阶导等于0的方法。
2.由梯度的定义知道,如果沿着梯度方向走,值会变大,朝梯度的反方向走,值会变小。

如图所示,我们假设函数是 ,那么如何使得这个函数达到最小值呢,简单的理解,就是对x求导,得到 y'=2x ,然后用梯度下降的方式,如果(参数的)初始值是(0的左边)负值,那么这时导数也是负值,用梯度下降的公式,使得x更加的靠近0,如果是正值的时候同理。注意:这里的梯度也就是一元函数的导数,高维的可以直接类推之
3.梯度下降法中,如果走的步长不是太大,函数一定会收敛到极值点。
5.θ是最优化要去求的一个(一组)参数,是一个(或者说是一组,比如说线性回归的斜率和截距参数)可学习的参数。
4.学习率在机器学习中是一个非常重要的超参数,也叫做步长,不能像θ一样通过最优化的方法去学习,步长不是神经网络可以习得的,是需要人为的进行选择的一个参数,所以叫做超参数。超参数就是它的值需要人为进行选择的参数。
5.如果参数的初始值在最优位置的左侧,那么斜率是负值,此时参数的更新方向是向着最优值的方向前进,假如参数的初始位置在最优参数的右侧,那么斜率是正值,此时参数的更新方向还是向着最优位置处前进。所以不必担心参数的初始化位置。
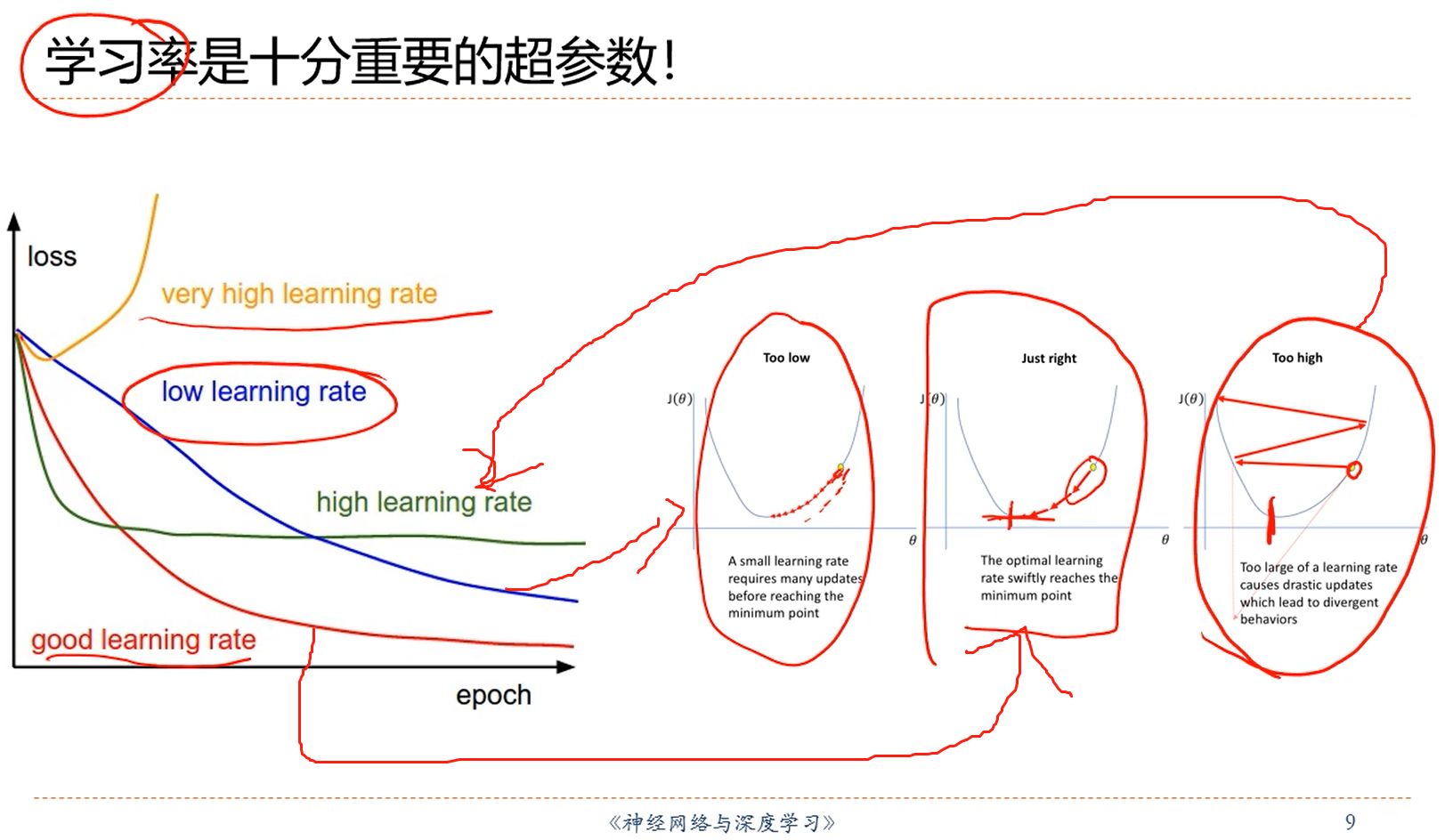
注解:
1.太大的学习率可能导致神经网络的参数变化收敛不到最优值。

注解:
1.针对无法充分利用计算机的并行计算能力这个缺点,一个折中的办法是采用小批量梯度下降法。
2.每次随机选取一小部分训练样本来计算梯度的话可能出现一个问题就是:由于是随机选择一小部分训练样本,可能造成最后有的训练样本没有被选择到,所以可能造成数据利用不完全的结果。
3.下图是解决方法:对所有训练样本进行一个随机打乱,再依次小批量采样。等所有样本都遍历一次后,再对所有训练样本进行一个第二次的随机排序,再依次小批量采样,这叫做第二个epoch.

注解:
1.这样的做法既保证了训练样本采集的随机性,又保证了所有训练样本都能参与计算。
2.第8步是说模型在验证集上的错误率不再下降,为何强调是在验证集上?why?