不通过正规方程的方式,通过的梯度下降的方式进行房价预测:
如果数据量少,特征数量少,可以用正规方程求解系数和预测值。
如果样本量大,特征数量多,不要用正规方程进行系数求解和预测,最好用梯度下降的方法进行迭代求解。


正规方程与随机梯度下降求得的权重和预测值的差值:
#load_boston里面的数值都是连续的 from sklearn.datasets import load_boston #从sklearn中的线性模型导入线性回归,SGD随机梯度下降 from sklearn.linear_model import LinearRegression,SGDRegressor from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler def mylinear(): """ 线性回归预测房子价格 :return: """ # 获取数据 lb=load_boston() # 分割数据集到训练集和测试集 x_train,x_test,y_train,y_test=train_test_split(lb.data,lb.target,test_size=0.25) #print(y_train) #打印训练样本 #print(" ") #print(y_test) #打印测试样本 # 对特征值进行标准化处理,目标值要不要进行标准化处理?答:也要标准化,因为特征值标准化之后,乘以小权重之后,得到 # 的值肯定也很小,这与原本的目标值相差会很大 # 特征值和目标值都必须进行标准化处理,实例化两个标准化API std_x=StandardScaler() #x_train=std_x.fit_transform(x_train.reshape(-1,13)) #x_test=std_x.fit_transform(x_test.reshape(-1,13)) x_train=std_x.fit_transform(x_train) x_test=std_x.fit_transform(x_test) # 对目标值进行标准化 std_y=StandardScaler() y_train=std_y.fit_transform(y_train.reshape(-1,1)) #样本训练标签y_train源程序提供的是1维数据, # 这里要做一个维度的形状转换,1维->2维,不知道有多少个样本,所以第一个参数是"-1",但是每个样本都只有一个目标值 y_test=std_y.transform(y_test.reshape(-1,1)) #y_train=std_y.fit_transform(y_train) #样本训练标签y_train源程序提供的是1维数据, # 这里要做一个维度的形状转换,1维->2维,不知道有多少个样本,所以第一个参数是"-1",但是每个样本都只有一个目标值 #x_test=std_y.transform(y_test) #estimator预测 # 首先使用正规方程求解方式预测结果: zhengguifunction=LinearRegression() zhengguifunction.fit(x_train,y_train) print("通过正规方程的方法求解的回归方程的系数是: ",zhengguifunction.coef_) # 打印出求解的权重参数 # 没有准确率了,但是可以使用求出的权重预测测试集样本的价格 #y_predict=lr.predict(x_test) #这个是根据测试样本预测的价格 # 之前标准化了,现在转化回去,不然预测的都是小值 y_zhengguifunction_predict = std_y.inverse_transform(zhengguifunction.predict(x_test)) # 这个是根据测试样本预测的价格 print("测试集里面每个测试样本中房子的预测价格是: ",y_zhengguifunction_predict) #打印出预测价格 # 通过梯度下降的方式进行房价预测: #lr=LinearRegression() sgdmethod=SGDRegressor() #SGD是随机梯度下降的意思,regressor就是回归的意思 sgdmethod.fit(x_train,y_train) sgdmethod.coef_=sgdmethod.coef_.reshape(1,-1) print("通过梯度下降的方法迭代求解的回归方程的系数是: ",sgdmethod.coef_) # 打印出求解的权重参数 # 没有准确率了,但是可以使用求出的权重预测测试集样本的价格 #y_predict=lr.predict(x_test) #这个是根据测试样本预测的价格 # 之前标准化了,现在转化回去,不然预测的都是小值 y_sgdmethod_predict = std_y.inverse_transform(sgdmethod.predict(x_test)) # 这个是根据测试样本预测的价格 y_sgdmethod_predict=y_sgdmethod_predict.reshape(-1,1) print("测试集里面每个测试样本中房子的预测价格是: ",y_sgdmethod_predict) #打印出预测价格 # 下面打印正规方程和随机梯度下降分别预测的权重系数的差值 print("通过正规方程方法求得的系数和随机梯度下降迭代求得的系数差值是:") for i in range(sgdmethod.coef_.shape[1]): print(sgdmethod.coef_[0][i]-zhengguifunction.coef_[0][i]) # 下面打印正规方程和随机梯度下降分别预测的房价的差值 print("通过正规方程方法预测的房价和随机梯度下降迭代预测的房价的差值是:") for i in range(y_sgdmethod_predict.shape[0]): print("%.1f"%abs((y_sgdmethod_predict[i][0]-y_zhengguifunction_predict[i][0])*10),"千元") #zhengguifunction.coef_ #sgdmethod.coef_ # y_zhengguifunction_predict #y_sgdmethod_predict # 下面打印正规方程和随机梯度下降分别预测的房子房价的差值 return None if __name__=="__main__": mylinear()
运行结果:
C:UsersTJAppDataLocalProgramsPythonPython37python.exe D:/qcc/python/mnist/fangjia_yuce.py 通过正规方程的方法求解的回归方程的系数是: [[-0.07806471 0.13680635 0.00612557 0.07940504 -0.24273661 0.23880737 0.01939301 -0.39550814 0.33298343 -0.27130526 -0.21892673 0.08405887 -0.46898053]] 测试集里面每个测试样本中房子的预测价格是: [[34.83401882] [42.71856525] [28.96837867] [18.87049196] [ 6.44105664] [33.52037252] [24.24531021] [13.83972449] [32.20048326] [22.13770312] [19.84497573] [32.42946675] [18.83364002] [18.16189868] [26.36841793] [25.3320747 ] [28.97962217] [33.96507178] [28.20661562] [12.26703709] [11.59487977] [16.16864481] [14.27993384] [19.75487482] [27.06912564] [28.37932392] [24.63338761] [20.68557423] [29.40414169] [22.03354357] [28.73369788] [19.9751999 ] [14.6073498 ] [20.86617225] [33.52891779] [15.98746627] [ 4.58824944] [34.54741596] [ 7.73881069] [13.98729272] [23.59663403] [ 6.76331182] [26.09158302] [13.96479334] [19.00926175] [17.13019262] [17.26943923] [17.89144945] [32.93492748] [16.8076371 ] [34.87100777] [12.60236188] [24.53281105] [40.07056545] [23.4309869 ] [35.03418257] [31.58136281] [28.5105472 ] [24.05969697] [29.56054411] [21.25675966] [33.78015261] [21.9899085 ] [13.74265295] [21.71182799] [15.13320398] [30.4816803 ] [32.44189334] [13.39869631] [28.46977342] [23.6474807 ] [18.69692121] [19.96567415] [ 9.40011522] [ 8.01505096] [19.51121264] [20.25830099] [20.83577269] [18.69611822] [24.36996467] [17.04282191] [23.22347398] [25.75621996] [22.43617536] [39.06668533] [30.89705128] [22.89050115] [17.95350406] [18.96670598] [ 8.15391495] [20.0827631 ] [22.26921212] [33.23764238] [12.68500107] [26.96957745] [28.90569033] [ 6.72022537] [20.24204765] [20.02382355] [17.30708419] [32.27350509] [14.84388084] [18.61944624] [26.0645984 ] [14.35484236] [26.15953954] [25.88208707] [29.37591371] [10.40113152] [20.24268164] [22.21918842] [10.47634501] [31.13235641] [22.15628122] [18.43224745] [ 3.52855077] [24.37223426] [21.76351407] [18.28053073] [18.59516033] [30.49567132] [32.95834454] [17.98715927] [41.47410967] [26.08453374] [24.49074713] [23.08284815]] 通过梯度下降的方法迭代求解的回归方程的系数是: [[-0.06345689 0.07560023 -0.07172121 0.09028746 -0.16368422 0.27464773 0.00326616 -0.29862426 0.14007983 -0.06501188 -0.21612084 0.09395852 -0.45686221]] 测试集里面每个测试样本中房子的预测价格是: [[36.04582384] [42.56272594] [30.22388555] [18.82115045] [ 5.6747144 ] [33.49059087] [23.527273 ] [15.07664402] [32.61777037] [21.5947436 ] [20.96869123] [30.92887169] [17.99456543] [18.35355786] [27.21833821] [24.52414375] [29.93989503] [35.14632423] [26.53970429] [12.3158328 ] [11.17452734] [16.83226797] [17.04360059] [20.78089159] [27.23580915] [26.6994182 ] [24.20394849] [19.31099684] [29.98966611] [21.80515638] [28.46468549] [22.30641824] [14.58569552] [20.60115043] [32.81513919] [13.10122983] [ 4.18104488] [33.57715392] [ 7.2898426 ] [14.05227046] [23.90703873] [ 9.11901447] [25.39574475] [12.40911421] [19.63131059] [16.72381376] [17.55532443] [17.85540039] [31.98352417] [15.42107563] [34.88049091] [12.85221502] [23.78997399] [41.1313183 ] [24.47348804] [33.48019224] [31.47133834] [27.87687435] [24.31468148] [28.48945019] [21.8148299 ] [33.5136172 ] [22.55479349] [15.72487998] [23.39681896] [17.67675439] [30.88089422] [30.66416478] [15.8722533 ] [30.33211797] [23.10511363] [19.63894312] [19.19197249] [ 8.75007509] [ 8.34072507] [19.51465065] [24.18989125] [20.84891877] [21.415611 ] [24.12359932] [15.55812498] [22.95613344] [25.57309324] [22.73217532] [38.80464814] [29.32552672] [22.72292558] [17.4883814 ] [19.07859683] [ 8.82543895] [20.77958339] [21.86056077] [31.88279613] [11.92924315] [26.98559299] [30.55100826] [ 5.39449749] [17.38829422] [19.51402633] [16.86371592] [32.115281 ] [14.26303666] [19.12361524] [25.72833362] [11.29780744] [26.11640777] [26.40055249] [29.21412449] [10.33706572] [20.27179017] [19.32783813] [ 9.54531938] [31.0939524 ] [22.50620989] [19.08528804] [ 3.28316433] [24.63738168] [22.13504877] [21.47986419] [17.81904187] [28.75744393] [33.88386459] [16.63682316] [40.16518079] [26.5225858 ] [25.74280295] [24.7974721 ]] 通过正规方程方法求得的系数和随机梯度下降迭代求得的系数差值是: 0.01460781600653839 -0.06120612210740542 -0.07784677554956843 0.010882424040643823 0.07905239353546109 0.0358403599012625 -0.016126847077433476 0.09688388004498172 -0.1929035959057229 0.20629338147671453 0.002805888287422731 0.0098996504769788 0.012118316786717098 通过正规方程方法预测的房价和随机梯度下降迭代预测的房价的差值是: 12.1 千元 1.6 千元 12.6 千元 0.5 千元 7.7 千元 0.3 千元 7.2 千元 12.4 千元 4.2 千元 5.4 千元 11.2 千元 15.0 千元 8.4 千元 1.9 千元 8.5 千元 8.1 千元 9.6 千元 11.8 千元 16.7 千元 0.5 千元 4.2 千元 6.6 千元 27.6 千元 10.3 千元 1.7 千元 16.8 千元 4.3 千元 13.7 千元 5.9 千元 2.3 千元 2.7 千元 23.3 千元 0.2 千元 2.7 千元 7.1 千元 28.9 千元 4.1 千元 9.7 千元 4.5 千元 0.6 千元 3.1 千元 23.6 千元 7.0 千元 15.6 千元 6.2 千元 4.1 千元 2.9 千元 0.4 千元 9.5 千元 13.9 千元 0.1 千元 2.5 千元 7.4 千元 10.6 千元 10.4 千元 15.5 千元 1.1 千元 6.3 千元 2.5 千元 10.7 千元 5.6 千元 2.7 千元 5.6 千元 19.8 千元 16.8 千元 25.4 千元 4.0 千元 17.8 千元 24.7 千元 18.6 千元 5.4 千元 9.4 千元 7.7 千元 6.5 千元 3.3 千元 0.0 千元 39.3 千元 0.1 千元 27.2 千元 2.5 千元 14.8 千元 2.7 千元 1.8 千元 3.0 千元 2.6 千元 15.7 千元 1.7 千元 4.7 千元 1.1 千元 6.7 千元 7.0 千元 4.1 千元 13.5 千元 7.6 千元 0.2 千元 16.5 千元 13.3 千元 28.5 千元 5.1 千元 4.4 千元 1.6 千元 5.8 千元 5.0 千元 3.4 千元 30.6 千元 0.4 千元 5.2 千元 1.6 千元 0.6 千元 0.3 千元 28.9 千元 9.3 千元 0.4 千元 3.5 千元 6.5 千元 2.5 千元 2.7 千元 3.7 千元 32.0 千元 7.8 千元 17.4 千元 9.3 千元 13.5 千元 13.1 千元 4.4 千元 12.5 千元 17.1 千元 C:UsersTJAppDataLocalProgramsPythonPython37libsite-packagessklearnutilsvalidation.py:724: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel(). y = column_or_1d(y, warn=True) Process finished with exit code 0
正规方程与随机梯度下降求得的权重和预测值的均方误差:
import tensorflow as tf def myregession(): """ 自实现一个线性回归预测 :return: None """ #1. 准备数据 x 特征值,[100,1], 100个样本,1个特征 # y 目标值 ,[100] x=tf.random_normal([10,1],mean=1.75,stddev=0.5,name="x_data")#这个是真实的特征值 y_true= tf.matmul(x,[[0.7]])+0.8 #先假设已经知道这个线性关系,其实现实中是不知道的,为了准备准据,才这样假设的 #注:矩阵相乘必须是二维的 # 2. 建立线性回归模型,一个特征,1个权重,一个偏置,y=wx+b #w,b需要随机初始化一个值,从这个地方开始优化,从这个地方计算损失,然后在当前状态下优化 #trainable参数是指定这个变量能否跟着梯度下降一起优化 weight= tf.Variable(tf.random_normal([1,1],mean=0.0,stddev=1.0),name="w",trainable=False) #权重必须定义成tf的变量,因为只有用变量定义才能优化,必须是二维的,所以定义成1行1列 bias=tf.Variable(0.0,name='b') y_predict=tf.matmul(x,weight)+bias # 3. 建立损失函数,求均方误差 loss=tf.reduce_mean(tf.square(y_true-y_predict)) # 3. 梯度下降优化损失,learning_rate:0~1,2,3,5,7,10 train_op=tf.train.ProximalGradientDescentOptimizer(0.1).minimize(loss) #定义个一个初始化变量的 op init_op=tf.global_variables_initializer() #通过会话运行程序 with tf.Session() as sess: # 初始化变量 sess.run(init_op) #打印最先随机初始化的权重和偏置 print("随机初始化的参数,权重为:%f,偏置为:%f"%(weight.eval(),bias.eval())) #注:weight,bias是不能直接打印的,因为它们是op # 运行优化 #循环训练,持续优化 for i in range(300): sess.run(train_op) print("第%d次运行优化后的参数,权重为:%f,偏置为:%f" % (i,weight.eval(), bias.eval())) return None if __name__=="__main__": myregession()
运行结果:
C:UsersTJAppDataLocalProgramsPythonPython37python.exe D:/qcc/python/mnist/fangjia_yuce.py
正规方程的均方误差是: 26.06901003802103 单位是:万元的平方
梯度下降的均方误差是: 26.74992321657139 单位是:万元的平方
注解:
- 这个例子里面,正规方程的方法好于随机梯度下降的方法。

注解:
- scikit-learn官网给的建议是:10万个样本以上要使用随机梯度下降迭代更新的方法求权值。
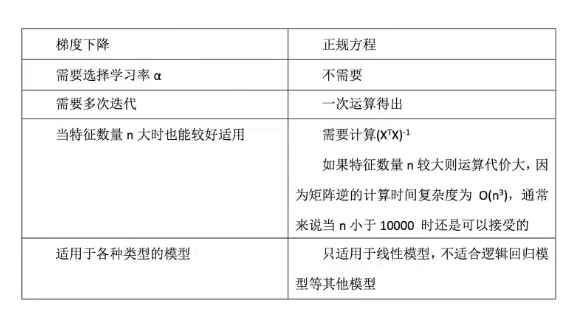

图片里面的字:不能解决过拟合问题。
过拟合问题:就是训练集表现好,测试集表现不好。