P34 线性回归的策略、优化、案例

http://bilibili.com/video/BV184411Q7Ng?p=34

 

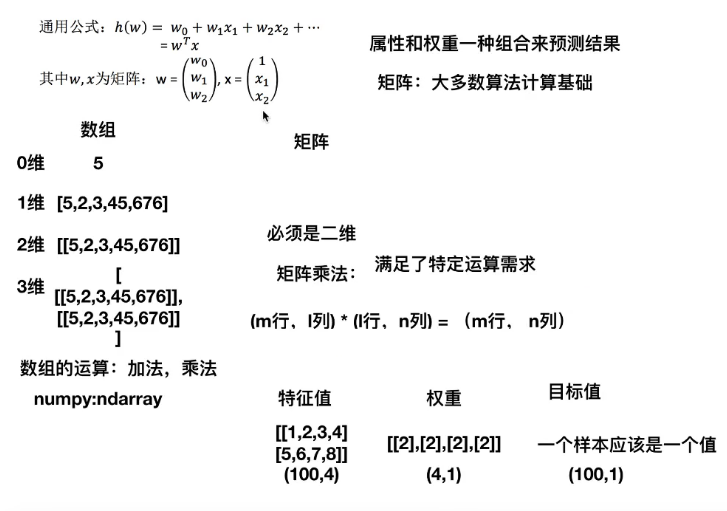
线性回归：就是找到合适的权阵，与每一个特征相乘，最后求和，得出要预测的目标值。

• 实际生活中，数据分布没有那么简单，并不是严格在一条直线上，所以即便使用机器学习用线性回归模型预测，也是有误差的。

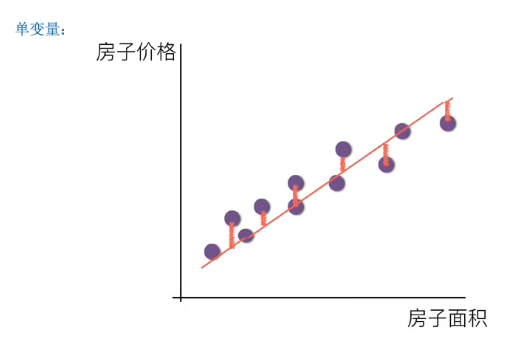
注解：

• 红色小线段就是预测误差。

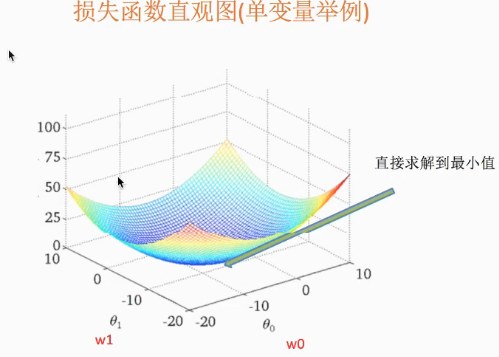
两个变量的三维情况：

• 黑色竖杠是预测偏差。
• 如果说，特征和目标值之间的关系是线性的话，那会以平面的形态显示。

至于4维、5维、。。。等高维度情况，线性关系叫超平面。

 

 

 

 注解:

• 可以直接求解到最小值。
• 但如果样本很多，特征也很多的话，求算速度是很慢的，甚至不收敛。

 

 

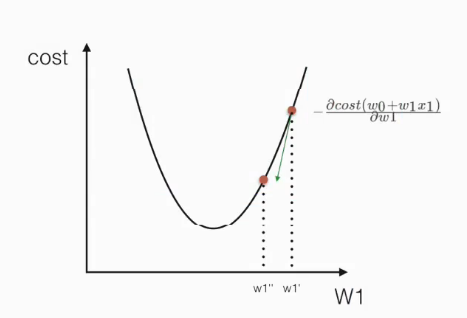
 下面这个动图展示了梯度下降的过程，也就是损失函数优化的过程：

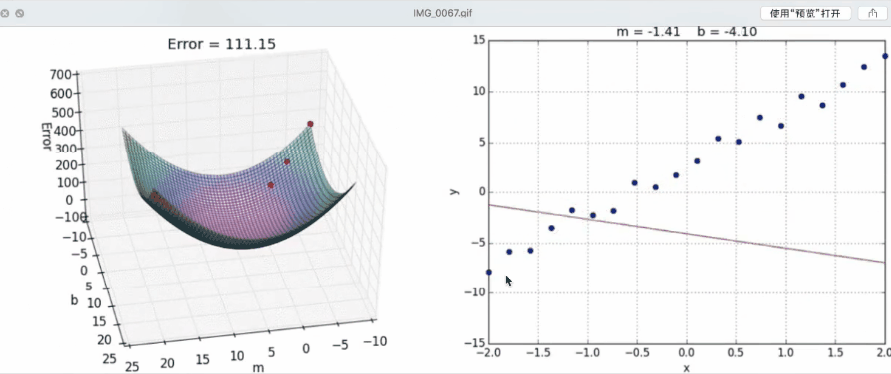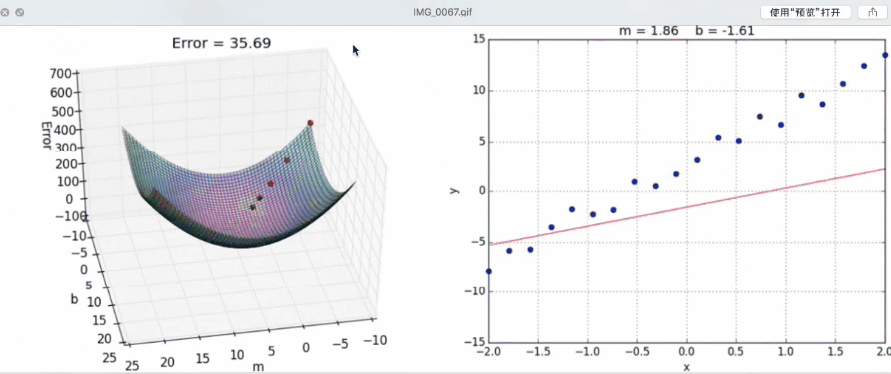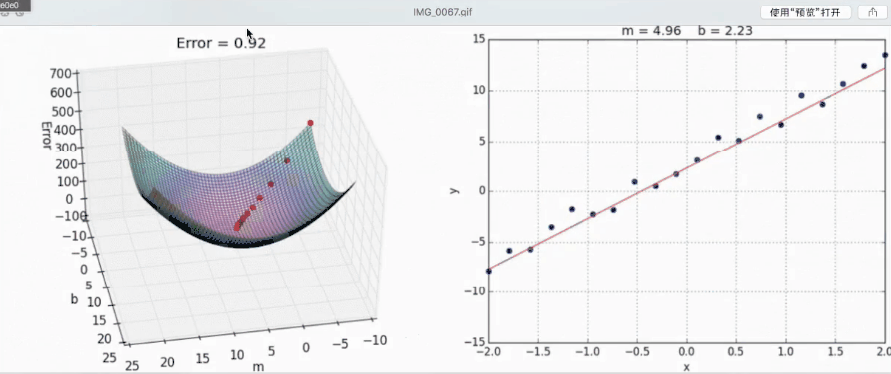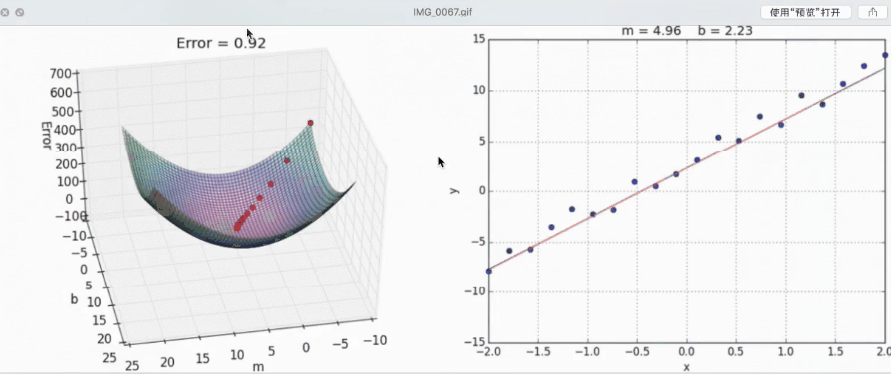
•  正规方程基本上不去使用。

 

•  回归系数就是要求解的最终的权值。

 

 

 

 

 

• 不对特征进行标准化的话，如果某个特征的值特别大，会导致h(w)特别大，会导致损失函数特别大，难以进行优化。

 

 下面利用Python代码进行实现：

#load_boston里面的数值都是连续的
from sklearn.datasets import load_boston
#从sklearn中的线性模型导入线性回归，SGD随机梯度下降
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler


def mylinear():
    """
    线性回归预测房子价格
    :return:
    """
    # 获取数据
    lb=load_boston()
    # 分割数据集到训练集和测试集
    x_train,x_test,y_train,y_test=train_test_split(lb.data,lb.target,test_size=0.25)

    #print(y_train) #打印训练样本
    #print("
")
    #print(y_test) #打印测试样本
    # 对特征值进行标准化处理，目标值要不要进行标准化处理？答：也要标准化，因为特征值标准化之后，乘以小权重之后，得到
    # 的值肯定也很小，这与原本的目标值相差会很大
    # 特征值和目标值都必须进行标准化处理,实例化两个标准化API
    std_x=StandardScaler()

    #x_train=std_x.fit_transform(x_train.reshape(-1,13))
    #x_test=std_x.fit_transform(x_test.reshape(-1,13))

    x_train=std_x.fit_transform(x_train)
    x_test=std_x.fit_transform(x_test)

    # 对目标值进行标准化
    std_y=StandardScaler()

    y_train=std_y.fit_transform(y_train.reshape(-1,1)) #样本训练标签y_train源程序提供的是1维数据，
    # 这里要做一个维度的形状转换，1维->2维，不知道有多少个样本，所以第一个参数是"-1",但是每个样本都只有一个目标值
    y_test=std_y.transform(y_test.reshape(-1,1))

    #y_train=std_y.fit_transform(y_train) #样本训练标签y_train源程序提供的是1维数据，
    # 这里要做一个维度的形状转换，1维->2维，不知道有多少个样本，所以第一个参数是"-1",但是每个样本都只有一个目标值
    #x_test=std_y.transform(y_test)




    #estimator预测

    # 首先使用正规方程求解方式预测结果：
    lr=LinearRegression()
    lr.fit(x_train,y_train)
    print(lr.coef_) # 打印出求解的权重参数

    # 没有准确率了，但是可以使用求出的权重预测测试集样本的价格
    y_predict=lr.predict(x_test) #这个是根据测试样本预测的价格
    print("测试集里面每个测试样本中房子的预测价格是：
",y_predict) #打印出预测价格


    return None





if __name__=="__main__":
    mylinear()

运行结果：

C:UsersTJAppDataLocalProgramsPythonPython37python.exe D:/qcc/python/mnist/fangjia_yuce.py
[[-0.12138184 0.12809057 0.05667483 0.0837892 -0.24314855 0.27338615
0.01904533 -0.31094097 0.32559218 -0.26246661 -0.23994406 0.085757
-0.41645344]]
测试集里面每个测试样本中房子的预测价格是：
[[-0.42701157]
[ 0.43362268]
[-0.29928423]
[-0.10157744]
[-0.07626557]
[-3.087107 ]
[-0.6876634 ]
[-0.10466244]
[-0.95795971]
[ 0.7411599 ]
[-0.38173128]
[ 1.60899307]
[ 1.93862376]
[ 1.33741743]
[-1.00712653]
[ 1.23199184]
[ 0.91964531]
[-0.74743857]
[-0.11836796]
[ 0.54314561]
[ 0.79422285]
[ 0.06709212]
[-1.23901357]
[-0.78247673]
[ 0.31380195]
[ 0.03398856]
[-0.71620802]
[-0.76306803]
[ 0.31018461]
[ 0.53926051]
[ 1.98573273]
[ 0.25602091]
[ 0.61098026]
[-1.37422017]
[ 0.884689 ]
[-2.12374473]
[-1.27598714]
[-0.19263116]
[ 0.06068922]
[ 1.05860473]
[-0.10551119]
[ 0.62565744]
[-0.21886903]
[-1.07651442]
[-0.19529375]
[-0.95162235]
[ 1.2631967 ]
[ 1.39053803]
[-0.28801539]
[ 0.23985705]
[-1.09911743]
[-1.56818781]
[-0.63572121]
[ 1.78778738]
[-0.49422611]
[-0.39505812]
[-1.27378989]
[-1.1007647 ]
[ 0.54669614]
[-1.21098113]
[ 0.37633332]
[ 0.84882076]
[-0.49285524]
[ 0.5680518 ]
[ 0.30043503]
[ 1.1413508 ]
[-1.23372619]
[ 1.40126443]
[-0.49827148]
[-0.30246881]
[-0.12940878]
[ 0.35849526]
[ 0.50727791]
[-0.62740161]
[-0.20940548]
[-0.23756779]
[-0.13440115]
[-0.29707494]
[-0.91878484]
[ 0.99115875]
[ 0.06708305]
[ 0.23299553]
[-0.85648758]
[ 1.14763492]
[-0.32219862]
[ 0.31755636]
[ 1.37080438]
[ 0.2601381 ]
[-0.90922894]
[-0.45329389]
[ 0.62075828]
[ 1.24946429]
[ 0.23070286]
[ 0.75917174]
[-0.5327008 ]
[-0.60701356]
[-0.12158806]
[ 0.65602487]
[ 0.24322484]
[ 0.29239153]
[-0.80919023]
[ 1.09635372]
[-0.35643465]
[-1.33533038]
[ 0.36164357]
[ 2.15519746]
[-0.67255352]
[ 0.68776144]
[-0.24054195]
[ 0.16212296]
[ 0.01786128]
[ 1.41410595]
[-0.81782078]
[ 0.3187114 ]
[ 0.5626069 ]
[-0.52345891]
[-1.14823269]
[ 1.2182153 ]
[ 0.22959761]
[-0.73730776]
[ 0.51536187]
[-1.08540422]
[ 0.16043968]
[-0.08886585]
[-0.71699509]
[ 0.0272304 ]
[ 0.10128338]]

Process finished with exit code 0

注解：

总共有13个系数，说明有13个特征，13个特征乘以相应的13个系数，就是目标值。

预测房子的价格都是小值，这是因为之前标准化了，还要用Inverse转换回去。

#load_boston里面的数值都是连续的
from sklearn.datasets import load_boston
#从sklearn中的线性模型导入线性回归，SGD随机梯度下降
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler


def mylinear():
    """
    线性回归预测房子价格
    :return:
    """
    # 获取数据
    lb=load_boston()
    # 分割数据集到训练集和测试集
    x_train,x_test,y_train,y_test=train_test_split(lb.data,lb.target,test_size=0.25)

    #print(y_train) #打印训练样本
    #print("
")
    #print(y_test) #打印测试样本
    # 对特征值进行标准化处理，目标值要不要进行标准化处理？答：也要标准化，因为特征值标准化之后，乘以小权重之后，得到
    # 的值肯定也很小，这与原本的目标值相差会很大
    # 特征值和目标值都必须进行标准化处理,实例化两个标准化API
    std_x=StandardScaler()

    #x_train=std_x.fit_transform(x_train.reshape(-1,13))
    #x_test=std_x.fit_transform(x_test.reshape(-1,13))

    x_train=std_x.fit_transform(x_train)
    x_test=std_x.fit_transform(x_test)

    # 对目标值进行标准化
    std_y=StandardScaler()

    y_train=std_y.fit_transform(y_train.reshape(-1,1)) #样本训练标签y_train源程序提供的是1维数据，
    # 这里要做一个维度的形状转换，1维->2维，不知道有多少个样本，所以第一个参数是"-1",但是每个样本都只有一个目标值
    y_test=std_y.transform(y_test.reshape(-1,1))

    #y_train=std_y.fit_transform(y_train) #样本训练标签y_train源程序提供的是1维数据，
    # 这里要做一个维度的形状转换，1维->2维，不知道有多少个样本，所以第一个参数是"-1",但是每个样本都只有一个目标值
    #x_test=std_y.transform(y_test)




    #estimator预测

    # 首先使用正规方程求解方式预测结果：
    lr=LinearRegression()
    lr.fit(x_train,y_train)
    print(lr.coef_) # 打印出求解的权重参数

    # 没有准确率了，但是可以使用求出的权重预测测试集样本的价格
    #y_predict=lr.predict(x_test) #这个是根据测试样本预测的价格
    # 之前标准化了，现在转化回去，不然预测的都是小值
    y_predict = std_y.inverse_transform(lr.predict(x_test))  # 这个是根据测试样本预测的价格
    print("测试集里面每个测试样本中房子的预测价格是：
",y_predict) #打印出预测价格


    return None





if __name__=="__main__":
    mylinear()

运行结果：

C:UsersTJAppDataLocalProgramsPythonPython37python.exe D:/qcc/python/mnist/fangjia_yuce.py
[[-0.05263847 0.12450021 0.03705734 0.07259102 -0.22649462 0.32516693
-0.0019832 -0.33145262 0.26878232 -0.23417706 -0.23636343 0.10264281
-0.36245772]]
测试集里面每个测试样本中房子的预测价格是：
[[28.47317056]
[21.35813894]
[30.17419749]
[17.7482451 ]
[19.64690509]
[20.39076351]
[18.25763475]
[14.00415639]
[16.50077092]
[18.60101432]
[19.73419316]
[27.09597009]
[17.48527456]
[25.74548193]
[24.44357381]
[18.56851961]
[23.45220109]
[22.63700048]
[17.66741066]
[19.98694207]
[27.05523847]
[20.06775203]
[18.20109741]
[25.66948708]
[ 9.4209829 ]
[32.0225063 ]
[23.77845029]
[11.4650438 ]
[18.66231814]
[29.34150763]
[31.94695628]
[19.07518871]
[14.29655445]
[27.73931211]
[29.14404646]
[25.55892608]
[29.41246153]
[27.85686452]
[34.53153413]
[32.80792313]
[19.81878332]
[16.51237249]
[24.12880237]
[28.60687153]
[23.77211424]
[23.62873641]
[17.22208598]
[14.62483881]
[18.90129796]
[12.43664433]
[18.83409379]
[20.89909858]
[16.33846083]
[36.24026031]
[20.01503989]
[27.40775107]
[20.88887132]
[33.46742391]
[23.40450245]
[27.096242 ]
[25.81993571]
[ 7.22354579]
[18.54769819]
[ 8.8854192 ]
[20.38254261]
[15.71357846]
[22.08392049]
[18.56050619]
[17.03366606]
[15.54221544]
[20.86508417]
[15.32363822]
[10.49211075]
[33.43496821]
[38.05057539]
[20.12081559]
[31.23200747]
[21.41099236]
[23.29835336]
[18.46583221]
[20.53867848]
[22.67137587]
[18.77026488]
[29.33557073]
[19.41787754]
[25.2552601 ]
[24.35689542]
[24.45035505]
[19.00881162]
[23.20901593]
[32.66685971]
[15.7055535 ]
[13.8733956 ]
[42.0581798 ]
[25.80742457]
[30.94031257]
[20.54570162]
[32.74431159]
[26.99216203]
[29.00370282]
[18.82195854]
[38.92280523]
[34.81636557]
[29.29280033]
[24.39009564]
[17.37751308]
[12.50084173]
[ 4.63284234]
[21.47197122]
[22.17191825]
[19.81095762]
[12.75379155]
[13.48270891]
[23.60696053]
[31.02726248]
[11.63183468]
[14.09859945]
[16.73132107]
[19.10490312]
[27.74661627]
[35.53892322]
[33.24303485]
[18.78668431]
[31.25728201]
[30.31539455]
[34.32436728]
[19.83956659]]

Process finished with exit code 0