为什么样本方差的分母是n-1?最简单的原因,是因为因为均值已经用了n个数的平均来做估计在求方差时,只有(n-1)个数和均值信息是不相关的。而你的第n个数已经可以由前(n-1)个数和均值 来唯一确定,实际上没有信息量。所以在计算方差时,只除以(n-1)。
总体方差(variance):总体中变量离其平均值距离的平均。一组数据
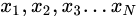

样本方差(variance):样本中变量离其平均值距离的平均。一组数据
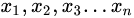
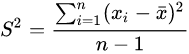
到这你可能会想:为什么样本方差中分母是n-1而不是n?我们假设是n看看

样本方差计算公式里分母为 ![]()
的目的是为了让方差的估计是无偏的。
无偏的估计(unbiased estimator)比有偏估计(biased estimator)更好是符合直觉的,尽管有的统计学家认为让mean square error即MSE最小才更有意义,这个问题我们不在这里探讨;不符合直觉的是,为什么分母必须得是
而不是  才能使得该估计无偏。
才能使得该估计无偏。
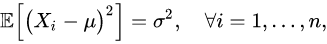
由此可得
 是方差的一个无偏估计,注意式中的分母不偏不倚正好是!这个结果符合直觉,并且在数学上也是显而易见的。
是方差的一个无偏估计,注意式中的分母不偏不倚正好是!这个结果符合直觉,并且在数学上也是显而易见的。
现在,我们考虑随机变量
![]()
的数学期望是未知
![]()
的情形。这时,我们会倾向于无脑直接用样本均值
替换掉上面式子中的
这样做有什么后果呢?后果就是,如果直接使用

作为估计,那么你会倾向于低估方差。
那么,在不知道随机变量真实数学期望的前提下,如何“正确”的估计方差呢?答案是把上式中的分母n换成n-1,通过这种方法把原来的偏小的估计“放大”一点点,我们就能获得对方差的正确估计了:
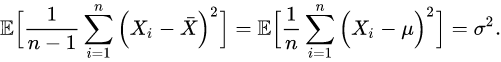
至于为什么分母是n-1而不是n-2或者别的什么数,原因如下:
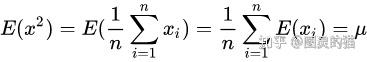
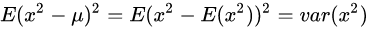
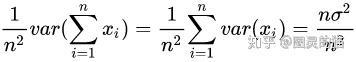
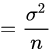
而
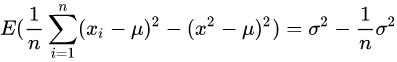
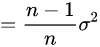
所以有
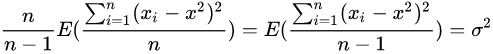
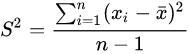
我们可以直观的看到随着样本总量n的增加,样本方差s会越来越接近总体方差。样本方差等于总体方差减样本均值的方差。如果用样本均值去估计总体均值,对总体方差的估计是有偏差的,偏差是样本均值的方差。需要做Bessel's correction去修正偏差,让偏差的期望等于0。
当n很大的时候,其实除以n和除以n-1的区别并不大。随着样本的增多,两者都会收敛到真实的总体方差。方差是协方差的特殊情况,就是当两个变量x与y相等时候的情况。既然我们已经知道样本方差为什么是除以n-1。那么样本协方差也是一样的道理。
总结一下:
- 分母是m-1的情况下,估计值是总体方差的无偏估计
- 分母是m的情况下,值是最大似然估计
- 分母是m+1的情况下,值是最小MSE(Mean Squared Error) 的估计
如果觉得样本够大,那么用m-1是不错的,因为在大样本下,参数的方差就算大一点儿也不会多多少,影响也不会大到哪儿去。
如果要保证信息利用充分,那我肯定选择最大似然估计的方差。如果样本数量较小,我就选择最小MSE,因为此时无偏性其实不是第一准则,因为无偏导致了大方差是不可取的行为。
参考资料:
作者:图灵的猫
链接:https://zhuanlan.zhihu.com/p/102043269
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。