1. 向量空间
向量空间表示一整个空间的向量,但不是任意向量的集合都能被称为向量空间。向量空间必须满足一定规则:该空间对空间内向量的线性组合(相加,数乘)封闭。也就是说如果一个向量集合所组成的空间满足两种操作(数乘、相加)且通过这两种操作及他们之间的线性组合后的向量仍然在这个集合所形成的空间中。那么我们就称它为向量空间。比如:v,w为向量空间内的向量,则向量3v 或 v+w 都仍然在此空间中,那么这个空间可称为向量空间。
比如 (所有的二维实向量)就是一个向量空间:
,
,
均在R^2向量空间中,对这3个2维向量进行线性组合,得到的向量仍在
向量空间中。反映在图像上:
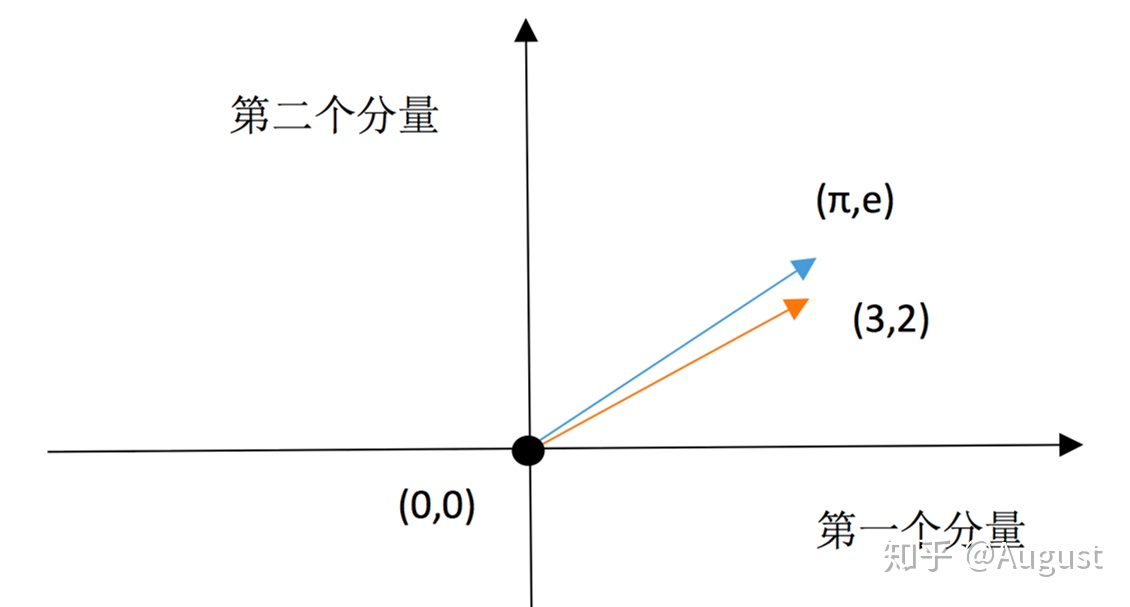
很明显, 的向量空间可以构成一个平面。这个向量空间存在的关键在于上图中平面上任何向量都在
的向量空间中。尤其是0向量,它存在于所有向量空间中。
同样,可以通过到三维向量空间,n 维向量空间
上。再举两个不是向量空间的例子:
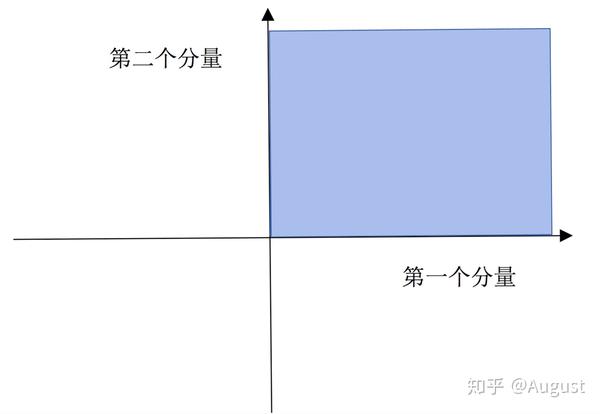
在上面图中,我们可以看到当我们尝试用-1和其中某个向量(除零向量)相乘时,其所得的向量一定不在第一象限中。可见,不满足数乘运算。所以,不是向量空间。
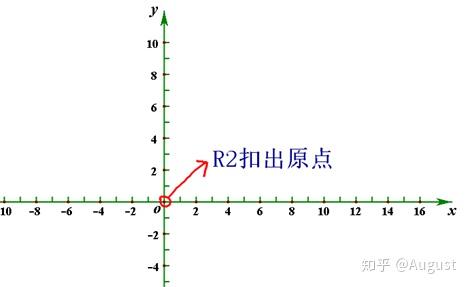
上图中是 中不含有0向量,那么当我们取一个向量和一个向量的反向向量相加时
所得到的零向量也不在其内部,可见,不满足相加运算,故其也不是向量空间
2. 子空间(subspace)
对于子空间,一个很好的解释属于向量空间的一部分,但是它同样满足向量空间的规则,也是一个向量空间。例如在 中的一条过原点的直线即为
的子空间。如图:
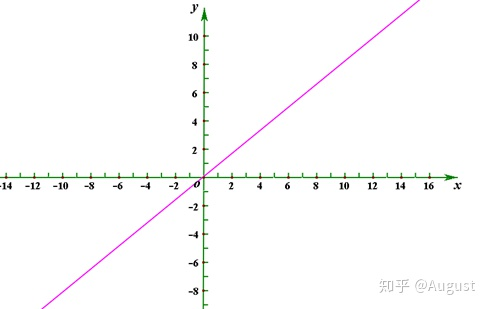
下面让我们去列举下在 (二维向量空间)和
(三维向量空间)中的所有的子空间。
中的子空间有:
本身
- 任何一条过原点(0,0)的直线(它就像
一样,却不同于
)
- 零向量
R^ 3中的子空间有:
本身
- 任何一个过原点(0,0,0)的平面
- 任何一条过原点(0,0,0)的直线
- 零向量
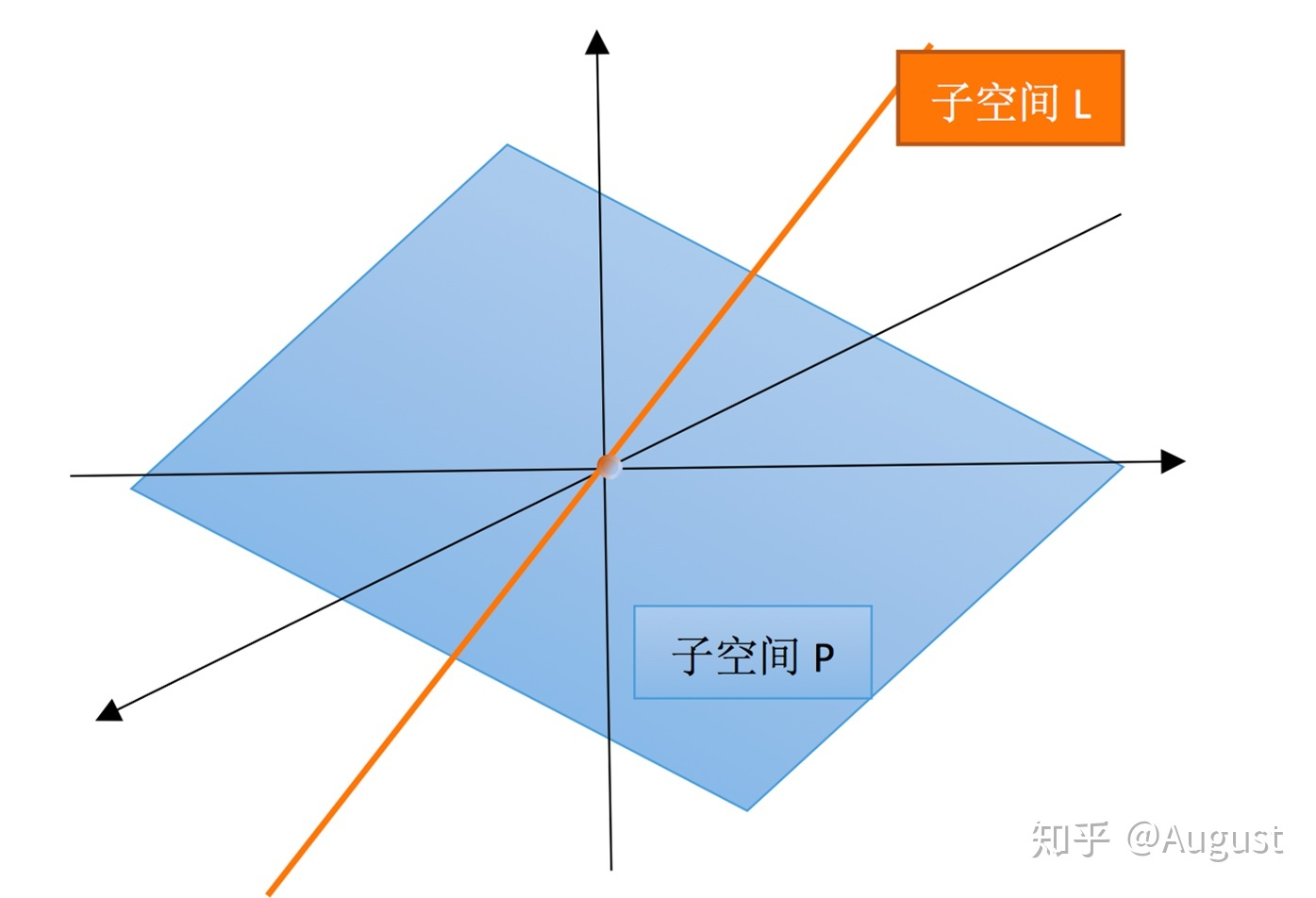
注意:子空间必须包含原点(零向量)
3. 矩阵的列空间(column space)
列空间是由一个矩阵的列向量所构造的子空间,下面我们给出一个矩阵A:
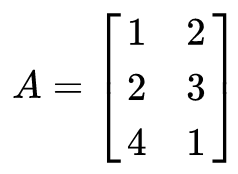
那么矩阵的两个列向量 以及它们的线性组合构成了
的子空间,我们称之为列空间。 记为C(A)。
因为不在同一条直线上,所以这个列空间表现在图像上就是一个过原点与这两个列向量的平面。也就是说A的列空间是三维空间中的一个平面。
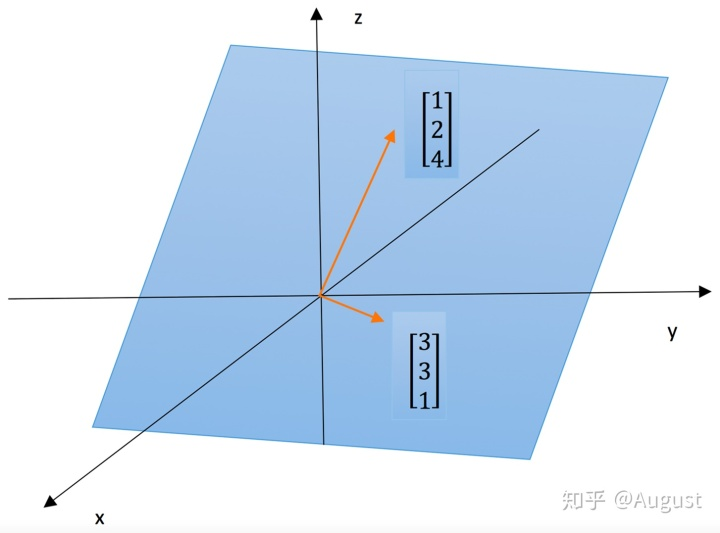
这里还要注意,如果矩阵的列向量两两之间是共线的,其列空间就是一条过原点的直线。
作者:August
链接:https://zhuanlan.zhihu.com/p/44099504
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。