Manacher算法其实是求字符串里面最长的回文。
①在学习该算法前,我们应该知道回文的定义:顺序读取回文和逆序读取回文得到的结果是一样的,如:abba,aba。
那么我们不难想到,在判断一个字符串str是否为回文之前,需要判断str中字符的个数的奇偶性。
②为了简化这一个冗杂的判断过程,Manacher算法对字符串str进行了预处理:
在每个字符之间插入一个一定不会出现的字符,如 ‘#’,'$'等。

为了后面我们更好地对字符串进行操作,我们可以在开头加一个标识符,标识字符串的开头(这里以'$'为例)。
到了这一步,无论原来字符串奇偶如何,现在都变成了偶数字符串。

③做完预处理之后,下一步就是求取 p[ ] 数组(随便取什么名字都可以)
p[ i ]数组的含义是存放以 s[ i ]为中心,最长回文的单边长度。我们来看一下下面的图来更好地理解:

以s[ 4 ] == 2为例,s[ 4 ]左右各移动一位 → 得到字符:# 和 # 相等;s[ 4 ]左右各移动两位 → 得到字符:1 和 2 不相等;
停止移动,因此p[ 4 ]位置该存放 2,以s[ 4 ]为中心最长回文的单边长度(包含s[ 4 ] )。
得到 p[ ] 数组之后我们就可以很简单地知道字符串str中的最长回文长度及最长回文了。
④ p[ ] 数组求取过程的技巧:
思考:在已经知道p [ 0 ] ~ p [ id ] 的情况下如何快速求取 p[ i ] 呢?
我们来看看下面这张图:以 s [ id ] 为中心的最长回文能够管辖的区域是s [ my ] ~ s [ mx ]
而 i 是落在了 my ~ mx 中。由于对称性,能够找到 j 使 s [ i ] == s [ j ] 同时 p [ i ] == p [ j ]
那么这个时候,可以直接令p [ i ] = p [ j ]。
同样地,在 id~mx 这个范围中的p [ ] 都能通过对称求出来。
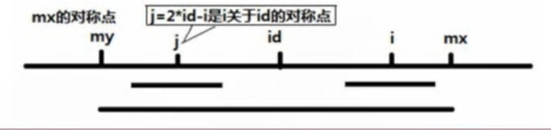
如果 i 落在mx右边的话,前半部分可以用对称,后半部分只能暴力求 p [ ]啦~
以上只是自己的一些拙见,如果有不正确的地方,欢迎指出。