题目:
7-1 稀疏矩阵 (30 分)
如果一个矩阵中,0元素占据了矩阵的大部分,那么这个矩阵称为“稀疏矩阵”。对于稀疏矩阵,传统的二维数组存储方式,会使用大量的内存来存储0,从而浪费大量内存。为此,可以用三元组的方式来存放一个稀疏矩阵。
对于一个给定的稀疏矩阵,设第r行、第c列值为v,且v不等于0,则这个值可以表示为 <r,v,c>。这个表示方法就称为三元组。那么,对于一个包含N个非零元素的稀疏矩阵,就可以用一个由N个三元组组成的表来存储了。
如:{<1, 1, 9>, <2, 3, 5>, <10, 20, 3>}就表示这样一个矩阵A:A[1,1]=9,A[2,3]=5,A[10,20]=3。其余元素为0。
要求查找某个非零数据是否在稀疏矩阵中,如果存在则输出其所在的行列号,不存在则输出ERROR。
输入格式:
共有N+2行输入: 第一行是三个整数m, n, N(N<=500),分别表示稀疏矩阵的行数、列数和矩阵中非零元素的个数,数据之间用空格间隔; 随后N行,输入稀疏矩阵的非零元素所在的行、列号和非零元素的值; 最后一行输入要查询的非0数据k。
输出格式:
如果存在则输出其行列号,不存在则输出ERROR。
输入样例:
在这里给出一组输入。例如:
10 29 3
2 18 -10
7 1 98
8 10 2
2
输出样例:
在这里给出相应的输出。例如:
8 10
分析:
在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵。
为了更好地定义稀疏矩阵,引入稀疏因子 t =num/(n*m)[其中num为矩阵中非零元素个数,n为矩阵行数,m为矩阵列数],
当t<=0.05时,该矩阵即可称作稀疏矩阵。
压缩稀疏矩阵的常见方法有两种:
1.利用三元组表压缩
优点:①代码简易;
②占用空间相对较小
缺点:①无法实现随机存储;
②在进行对矩阵的操作(如矩阵的乘法/加法)矩阵中数据改变后,需要重新定义三元组表,不具有通用性,不灵活。
2.利用十字链表压缩
优点:①能够实现随机存储;
②对于任意矩阵具有通用性
缺点:①代码实现困难;
②占用空间相对较大
分析之后我们发现,相对于利用三元组表压缩稀疏矩阵,利用十字链表压缩应用的范围更为广阔,更具有实际操作意义。
这里我们采取十字链表方式进行压缩。
十字链表核心(难点):
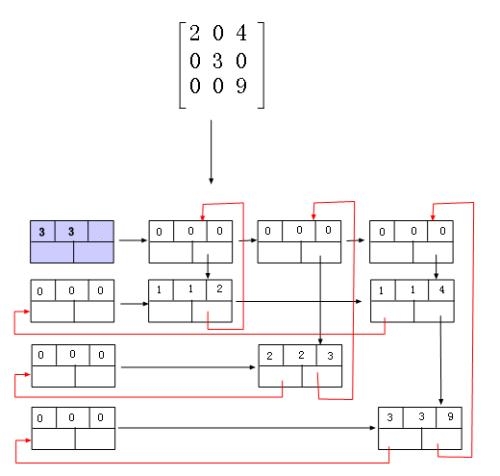
1.节点定义
(1)非零元素节点:
我们可以知道,十字链表说到底还是若干个循环链表,那么在创建十字链表之前我们需要构建一个合适的节点
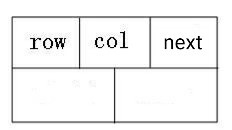
所需信息:行(row)、列(col)、值(val),该节点又要连接行的下一个节点(*right)以及列的下一个节点(*down)
如图:

(2)头节点定义
头节点与非零元素不同的是节点中row的位置存放的是原矩阵所有行数,col的位置存放的是原矩阵所有列数,且头节点需要指向一个指针数组(用于表示行列链表头)。
所需信息:行(row)、列(col)、指向指针数组*h[]的指针(*next)
如图:
(3)行列链表头节点定义:
行列链表头的表示其实是利用指针数组实现的(存放指针的数组)*h[],这里为了方便,我们称为行列头指针。
所需信息:指向下一个行列链表头节点的指针(*next)、指向该行第一个非零元素的指针(*right)、指向该列第一个非零元素的指针(*down)
如图:

综上所述,为了实现定义节点操作时的一致性,我们会将节点定义如下图:

2.行列链表头节点在十字链表中的理解
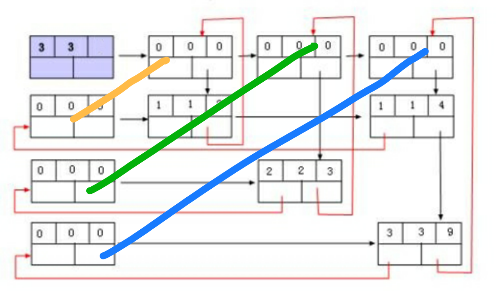
连线两端一个看上去像行头、另一个看上去像列头,其实这两个都是同一个*h[]。
我看到有建立两个指针数组的博客 https://blog.csdn.net/zhuyi2654715/article/details/6729783,即行链表头数组和列链表头数组,
想必是误解了图的意思。
我是那么理解的:

3.当行/列中没有非零元素时的表示
前面提到,这是由若干个循环链表构成的十字链表,那么在空行/列的时候可以用行列头指针指向它自己本身来表示。
同理,当为行/列末时,最后一个节点的指针right/down必然是指向行/列头节点的。
代码:
#include<iostream> using namespace std; //定义十字链表节点 typedef struct matrinode{ int i, j; struct matrinode *right, *down; union{ int value; struct matrinode *next; }tag; }matrinode; //创建十字链表 //传入值:头节点指针,原矩阵行数,原矩阵列数 void createlist(matrinode *&head, int row, int column) { int max = (row>column)?row:column;//取行列的最大值 //定义指针数组(用于表示行列头),p、q、r辅助指针 matrinode *h[max], *p, *q, *r; head = new matrinode;//申请头节点空间 head->i = row;//将行数、列数存入头节点 head->j = column; r = head; //行列链表头 int count; for(count = 1; count<max+1; count++){//为了表示矩阵的行数和列数,这里从1开始计数 h[count] = new matrinode;//给行列链表头申请空间 h[count]->down = h[count]->right = h[count]; h[count]->i = h[count]->j = 0; r->tag.next = h[count];//head->h[1]->h[2]->...->h[max] r = h[count]; } r->tag.next = head;//最后一个行列链表头节点指向head int num;//非零元素个数 int i, j, v; cin>>num; for(count=1; count<num+1; count++){ p = new matrinode; cin>>i>>j>>v; p->i = i; p->j = j; p->tag.value = v; /*这里插入非零元素有两种情况:(以在某行插入为例) ①当行链表为空(q->right == h[count])—或改元素列序数最大时 -> 插入到最后; ②非以上情况 -> 插入到某两节点中间 */ //行插入 q = h[count]; while(q->right != h[count] && q->right->j < j){ q = q->right; } p->right = q->right; q->right = p; //列插入 q = h[count]; while(q->down != h[count] && q->down->i < i){ q = q->down; } p->down = q->down; q->down = p; } } //查找是否有符合条件的值 void search(matrinode *head) { int value;//输入需要查找的值 cin>>value; matrinode *h, *p;//定义两个辅助结点 h = new matrinode; p = new matrinode; h = head->tag.next;//h指向h[1] p = h->right;//p指向h[1]第一行第一个元素 int flag = 0;//flag == 0表示找不到匹配值 int i, j;//若找到满足条件的值时,i、j存放该值的行和列 while(h->tag.next != head){//当前行不是最后一行时 if(p == h){//若该行为空 h = h->tag.next;//移到下一行 p = h->right; }else{//若该行非空 if(p->tag.value != value){//若p节点存放的值!=需要查找的值时 p = p->right;//p移动到该行下一个 }else{//找到满足条件的值时 i = p->i; j = p->j; flag = 1; cout<<i<<" "<<j; break; } } } if(flag == 0){ cout<<"ERROR"; } } int main(){ matrinode *head; int row, column; cin>>row>>column; createlist(head, row, column); search(head); return 0; }
总结:
为了学会十字链表,查阅了很多资料,每份资料都不尽相同。这份代码是我打的第四份代码,因为参考的博客都不太一样,
比如有的博客会用到struct来定义一个十字链表,有的博客更喜欢用class囊括所有。从一开始的照猫画虎,到逐渐理解算法的核心思想,
需要经过不断的锻造,这也可能是我与代码互相折磨、互相成长的过程吧!
参考资料:
1.https://blog.csdn.net/xiangxizhishi/article/details/79119532
2.https://blog.csdn.net/TheLegendOfZelda/article/details/80221922