20165315 结对编程练习_四则运算(阶段总结)
需求分析
- 对需求的理解
- 支持真分数的四则运算
- 支持多运算符
- 能手动输入n道题目,n由使用者输入
- 后续拓展的可能
- 能随机生成n道题目,n由使用者输入
- 能够判断正误,错误时能提醒并输出正确答案
- 能计算出正确率
- 能多次生成题目,直到使用者选择退出
- 题目去重
- 处理生成题目并输出到文件
- 完成题目后从文件读入并判题
- 多语言支持:
简体中文,繁體中文,English
设计思路
先从键盘输入生成题目数,进入循环,从键盘输入算式,利用ChangeExpress方法将输入的算式转换为字符串,再用MyDcRational方法对算式进行后缀式计算,将分子分母分别输出后进行判断,若分母为1,则直接输出分子;若分母不为一,则输出分数形式。
UML图如下:
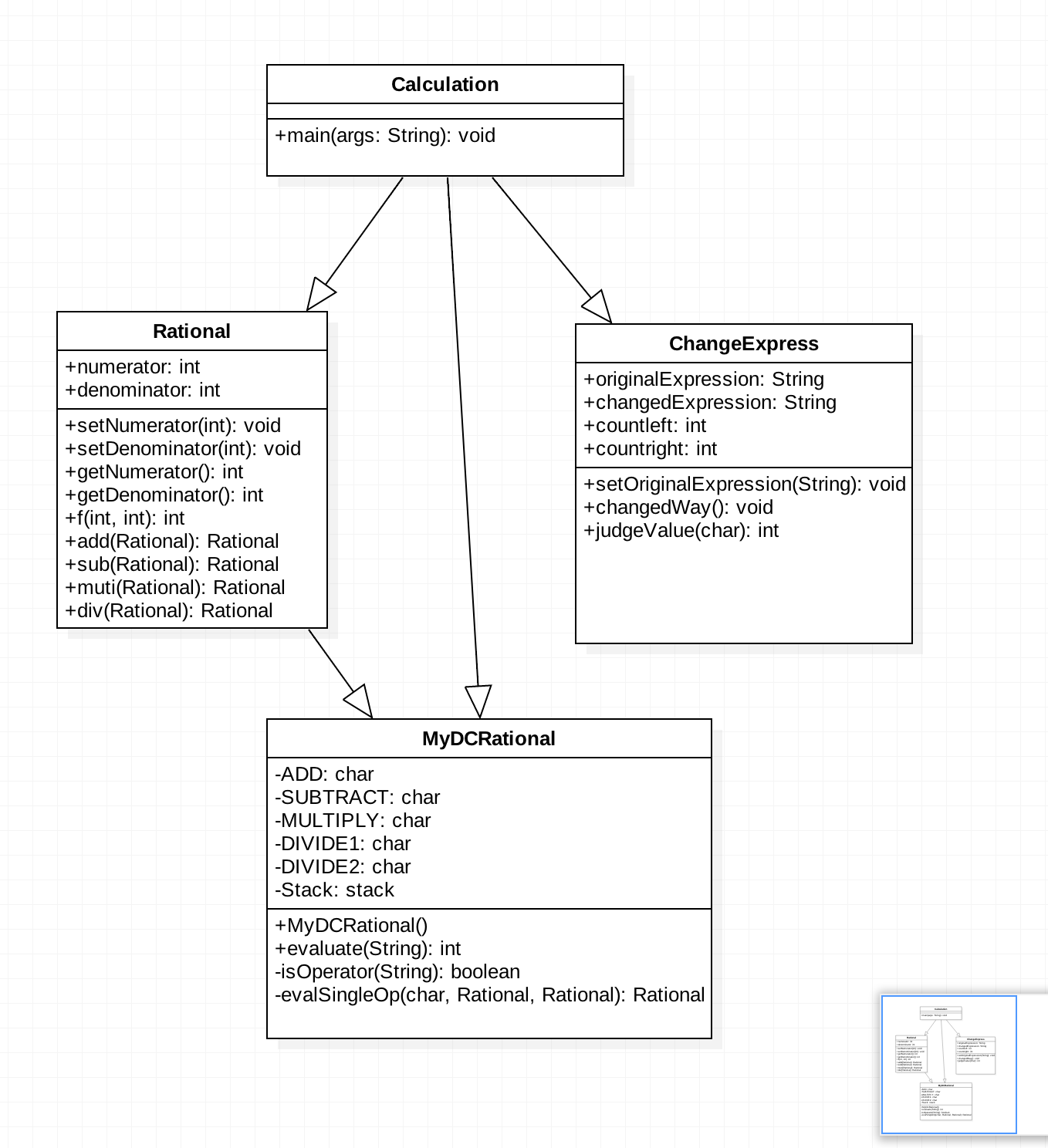
实现过程中的关键代码解释
- 进行带括号的四则运算:需要将输入的字符串更改为后缀式并进行计算。学习了[2016-2017-2 《Java 程序设计》课堂实践项目]之后,发现老师的参考代码
MyDC.java,原理是:利用空格作为分隔符将后缀式表达的字符串进行分割,遇到操作数就压栈,遇到操作符就弹出栈顶的两位操作数进行运算,再将运行结果压栈,直到没有下一个分割好的字符串,输出结果:
import java.util.StringTokenizer;
import java.util.Stack;
public class MyDC
{
/** constant for addition symbol */
private final char ADD = '+';
/** constant for subtraction symbol */
private final char SUBTRACT = '-';
/** constant for multiplication symbol */
private final char MULTIPLY = '*';
/** constant for division symbol */
private final char DIVIDE = '/';
/** the stack */
private Stack<Integer> stack;//存放操作数的栈,且只能存放Integer型
public MyDC()
{
stack = new Stack<Integer>();
}
public int evaluate (String expr)
{
int op1, op2, result = 0;
String token;
StringTokenizer tokenizer = new StringTokenizer (expr);//划分表达式
while (tokenizer.hasMoreTokens())
{
token = tokenizer.nextToken();//将算数表达式以空格为分隔符进行分解
if (isOperator(token))//见下方isOperateor方法,当是运算符的时候进入if语句
{
op2 = (stack.pop()).intValue();
op1 = (stack.pop()).intValue();//弹出最上面两个操作数
result = evalSingleOp (token.charAt(0), op1, op2);//见下方evaSingleOp方法
stack.push (new Integer(result));//将计算结果压栈
}
else
stack.push (new Integer(Integer.parseInt(token)));//操作数入栈
}
return result;//输出结果
}
private boolean isOperator (String token)//判断是否为运算符,注意用equal语句比较字符串
{
return ( token.equals("+") || token.equals("-") ||
token.equals("*") || token.equals("/") );
}
private int evalSingleOp (char operation, int op1, int op2)
{
int result = 0;
switch (operation)
{
case ADD:
result = op1 + op2;
break;
case SUBTRACT:
result = op1 - op2;
break;
case MULTIPLY:
result = op1 * op2;
break;
case DIVIDE:
result = op1 / op2;
}
return result;
}
}
-
考虑题目要求为能进行分数运算,想起来教材第四章代码
Rational.java可以保留分式进行加、减、乘、除、分数约分等运算,但书上代码a. 没有考虑到分母为零或者除数为零的情况,所以加以改动,在此情况下打印错误“分子/除数不能为0并退出运算”;
b. 分母为负分子为正时的输出没有将符号提前,进行符号提前:
public class Rational{//有理数
int numerator=1;//分子
int denominator=1;//分母
void setNumerator(int a){//设置分子
int c=f(Math.abs(a),denominator);//计算最大公约数
numerator=a/c;
denominator=denominator/c;
if (numerator<0&&denominator<0) {
numerator=-numerator;
denominator=-denominator;
}
}
void setDenominator(int b){//设置分母
int c=f(numerator,Math.abs(b));//计算最大公约数
numerator=numerator/c;
denominator=b/c;
if (numerator<0&&denominator<0) {
numerator=-numerator;
denominator=-denominator;
}
else if (numerator>0&&denominator<0){
numerator=-numerator;
denominator=-denominator;
}
}
int getNumerator(){
return numerator;
}
int getDenominator(){
return denominator;
}
int f(int a,int b){//求a,b的最大公约数
if (a==0) {
return 1;//c为分母不能为0
}
if (a<b) {//令a>b
int c=a;
a=b;
b=c;
}
int r=a%b;
while (r!=0) {
a=b;
b=r;
r=a%b;
}
return b;
}
Rational add(Rational r){//加法运算
int a=r.getNumerator();//返回有理数r的分子
int b=r.getDenominator();//返回有理数r的分母
int newNumerator=numerator*b+denominator*a;//计算出新分子
int newDenominator=denominator*b;//计算出新分母
Rational result=new Rational();
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
return result;
}
Rational sub(Rational r){//减法运算
int a=r.getNumerator();
int b=r.getDenominator();
int newNumerator=numerator*b-denominator*a;
int newDenominator=denominator*b;
Rational result=new Rational();
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
return result;
}
Rational muti(Rational r){//乘法运算
int a=r.getNumerator();
int b=r.getDenominator();
int newNumerator=numerator*a;
int newDenominator=denominator*b;
Rational result=new Rational();
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
return result;
}
Rational div(Rational r){//除法运算
int a=r.getNumerator();
int b=r.getDenominator();
Rational result=new Rational();
if (a==0) {
System.out.println("分母/除数不能为0");
result.setNumerator(0);
System.exit(0);
}
else{
int newNumerator=numerator*b;
int newDenominator=denominator*a;
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
}
return result;
}
}
- 根据
MyDC.java与Rational.java进行综合与改动,完成代码MyDcRational.java,将整数与小数运算改为分数与整数的后缀式运算:
import java.util.StringTokenizer;
import java.util.Stack;
public class MyDcRational
{
/** constant for addition symbol */
private final char ADD = '+';
/** constant for subtraction symbol */
private final char SUBTRACT = '-';
/** constant for multiplication symbol */
private final char MULTIPLY = '*';
/** constant for division symbol */
private final char DIVIDE = '/';
/** the stack */
private Stack stack;//存放操作数的栈
public MyDcRational()
{
stack = new Stack();
}
public Rational evaluate (String expr)
{
Rational op1=new Rational();
Rational op2=new Rational();
Rational result=new Rational();
result.setNumerator(0);
String token;
StringTokenizer tokenizer = new StringTokenizer (expr);//划分表达式
while (tokenizer.hasMoreTokens())
{
token = tokenizer.nextToken();//将算数表达式分解的
if (isOperator(token))//见下方isOperateor方法,当是运算符的时候进入if语句
{
op2 = (Rational) stack.pop();
op1 = (Rational)stack.pop();//弹出最上面两个操作数
result = evalSingleOp (token.charAt(0), op1, op2);//见下方evaSingleOp方法
stack.push (result);//将计算结果压栈
}
else{
Rational num=new Rational();
num.setNumerator(Integer.parseInt(token));//将操作数由string转变为Rational
stack.push (num);//操作数入栈
}
}
return result;//输出结果
}
private boolean isOperator (String token)//判断是否为运算符,注意用equal语句比较字符串
{
return ( token.equals("+") || token.equals("-") ||
token.equals("*") || token.equals("/") );
}
private Rational evalSingleOp (char operation, Rational op1, Rational op2)
{
Rational result=new Rational();
result.setNumerator(0);
switch (operation)
{
case ADD:
result = op1.add(op2);
break;
case SUBTRACT:
result = op1.sub(op2);
break;
case MULTIPLY:
result = op1.muti(op2);
break;
case DIVIDE:
result = op1.div(op2);
break;
default:
System.out.println("Error!");
}
return result;
}
}
- 要利用
MyDcRational.java完成运算就需要将前缀式改成后缀式,具体思路在[2016-2017-2 《Java 程序设计》课堂实践项目]中有明确的说明:
- 设立一个栈,存放运算符,首先栈为空;
- 从左到右扫描中缀式,若遇到操作数,直接输出,并输出一个空格作为两个操作数的分隔符;
- 若遇到运算符,则与栈顶比较,比栈顶级别高则进栈,否则退出栈顶元素并输出,然后输出一个空格作分隔符;
- 若遇到左括号,进栈;若遇到右括号,则一直退栈输出,直到退到左括号止。
- 当栈变成空时,输出的结果即为后缀表达式。
根据上述思路,完成代码ChangeExpress.java,将前缀式改为后缀式,并且完成分析括号匹配的功能,若左右括号不匹配,输出错误并退出程序运行:
import java.util.*;
public class ChangeExpress{
String originalExpression;
String changedExpression= "";
int countLeft=0,countRight=0;
public void setOriginalExpression(String str){
originalExpression=str;
}
public void changedWay(){
Stack stackChange=new Stack();//创立栈
int opValue []=new int[100];
for (int i=0;i<originalExpression.length() ;i++) {
char chi=originalExpression.charAt(i);
if (chi>='0'&&chi<='9'){
changedExpression=changedExpression+chi;
}
else if (chi=='+'||chi=='-'||chi=='*'||chi=='/') {
changedExpression=changedExpression+" ";//有运算符,数字之间就要有空格,否则是一个整体
if (stackChange.empty()){//栈为空直接压栈
stackChange.push(chi);
}
else if (judgeValue(chi)>=judgeValue((char)stackChange.peek())) {//运算级别高或者相等压入栈
stackChange.push(chi);
}
else{
changedExpression=changedExpression+ String.valueOf(stackChange.pop())+" ";//否则直接进入字符串,空格分割运算符
i--;
}
}
else if(chi=='('){
countLeft++;
stackChange.push(chi);//左括号压栈
}
else if(chi==')'){
changedExpression+=" ";
countRight++;
while((char)stackChange.peek()!='('){//直到(为止
changedExpression=changedExpression+ String.valueOf(stackChange.pop())+" ";//弹出栈内东西,空格分割
}
stackChange.pop();
}
}
changedExpression+=" ";
while(!stackChange.empty()){
changedExpression=changedExpression+String.valueOf(stackChange.pop())+" ";
}
if (countLeft!=countRight) {
System.out.println("括号不匹配");
System.exit(0);
}
}
public int judgeValue(char c){
int value=0;
switch(c){
case '(':
value=1;
break;
case '+':
case '-':
value=2;
break;
case '*':
case '/':
value=3;
break;
case ')':
value=4;
default:
value=0;
}
return value;
}
}
- 最后编写主函数代码
Calculation.java,实现功能有:运算式输入、运算、结果输出:
import java.util.*;
public class Calculation{
public static void main(String[] args) {
Scanner reader=new Scanner(System.in);
Rational result=new Rational();
System.out.println("请输入运算式");
String str=reader.nextLine();
ChangeExpress change=new ChangeExpress();
change.setOriginalExpression(str);
//System.out.println(change.originalExpression);
change.changedWay();//后缀式化
//System.out.println(change.changedExpression);
MyDcRational calculate=new MyDcRational();//后缀式计算
result=calculate.evaluate(change.changedExpression);
int a=result.getNumerator();
int b=result.getDenominator();
if (b==1){
System.out.println("result="+a);
}
else{
System.out.println("result="+a+"/"+b);
}
}
}
测试方法
由于我们的代码大部分都是无返回值的void类型,故进行测试的类只有如下:
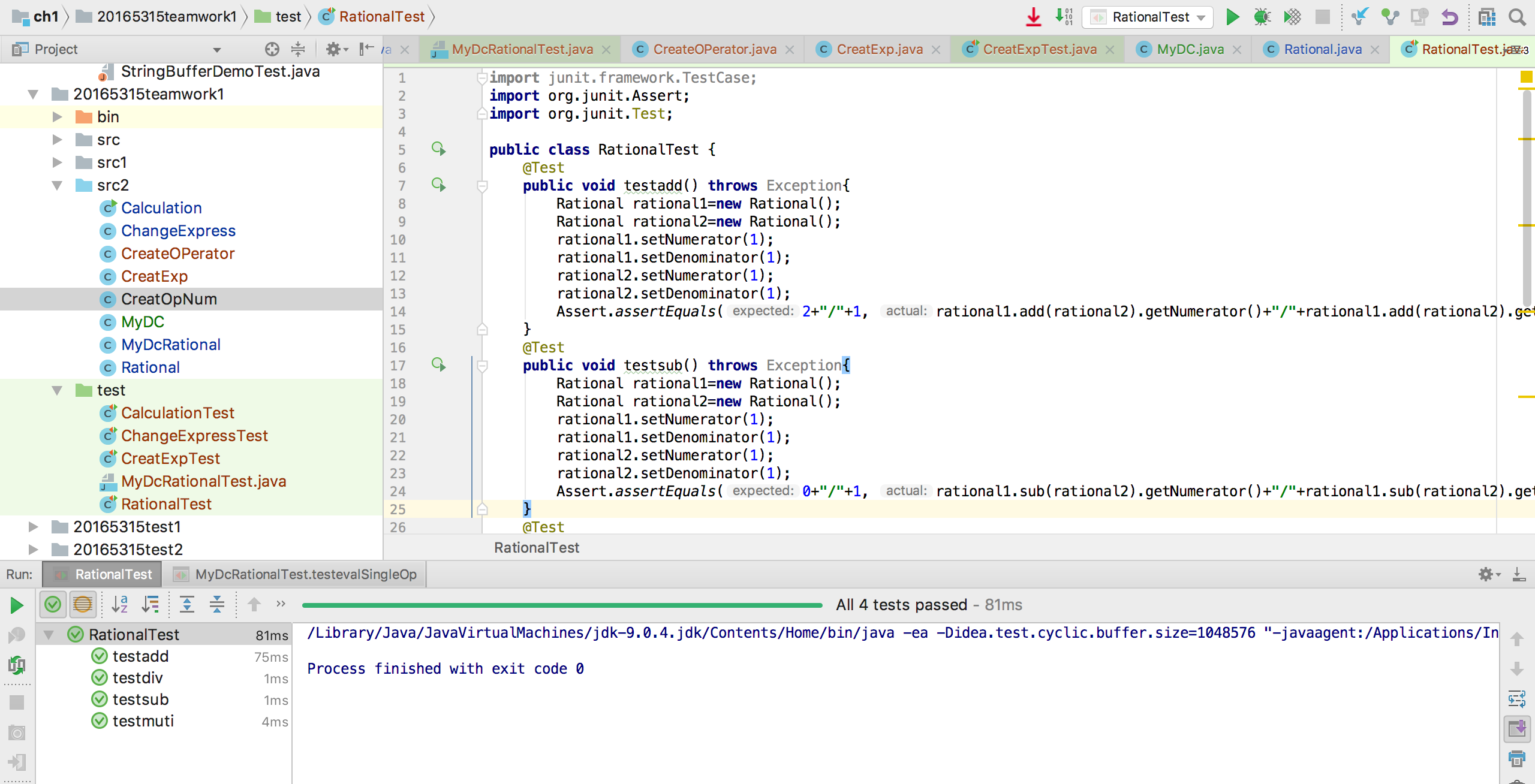

运行过程截图
- 正常情况
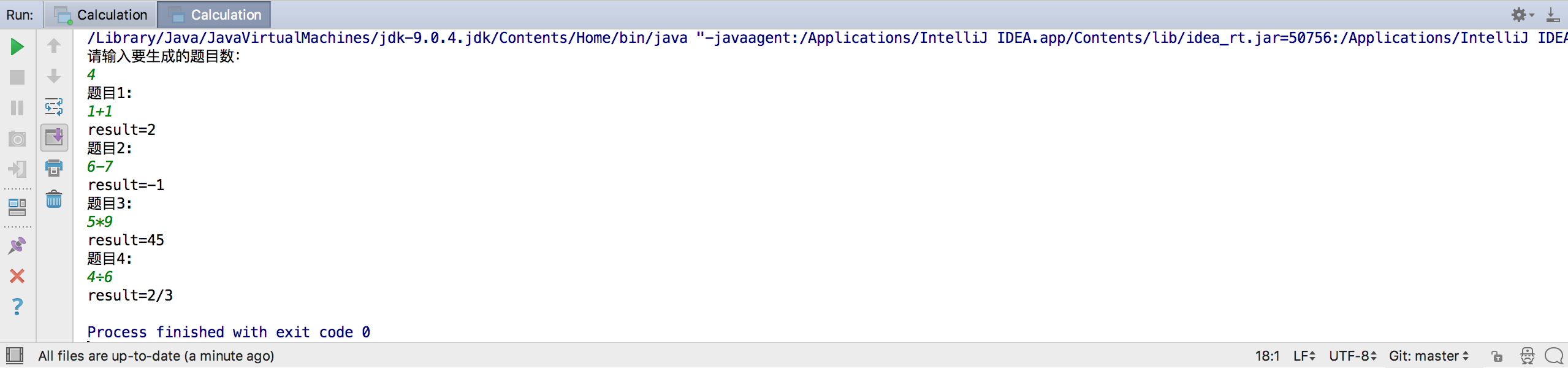
- 边界情况
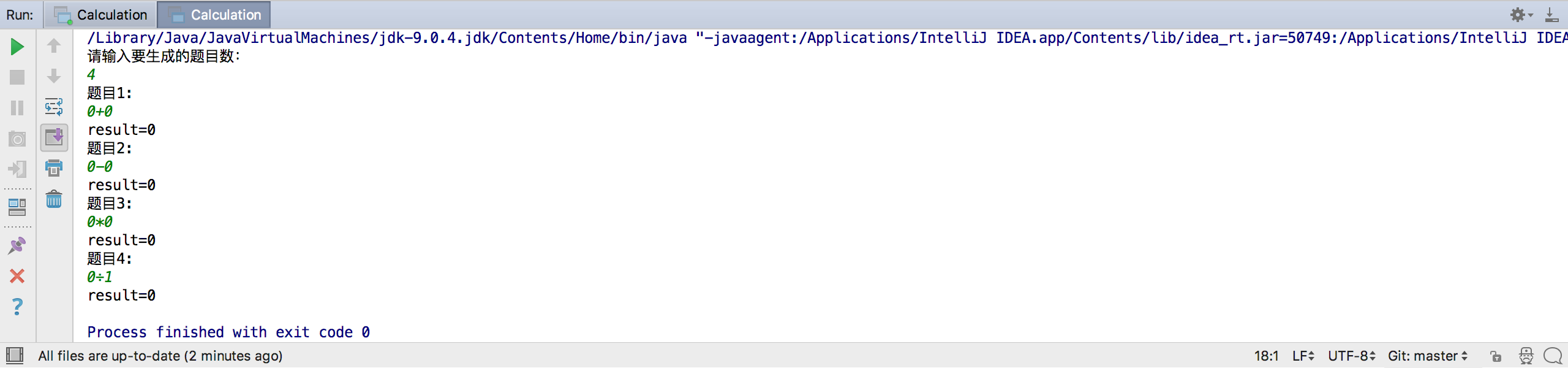
- 异常情况

代码托管地址
https://gitee.com/BESTI-IS-JAVA-2018/ch1/tree/master/20165315teamwork1/src2
遇到的困难及解决方法
由于我的结对伙伴上次实验是做的四则运算,故我们一开始便是基于上次实验开始做这次的结对编程
- 由于题目中要求使用的除号是
÷,而之前的代码则是使用的/,所以在辨别分数和除号时出了一些问题
解决方法:
新增了一个运算符÷,并设置它的优先级等等,将之前程序中使用的/对应改成÷
- 这次题目有很多新增的要求,为了防止主函数太过冗杂,我们认为应该重新设置一个主类,这就需要修改很多代码,容易出bug
解决方法:
我和结对伙伴已经做了大概的思路,即再新增Language类、Judge类等等,将在下周的总结中解决
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 30 | 40 |
| Development | 开发 | ||
| ·Analysis | · 需求分析 (包括学习新技术) | 60 | 90 |
| ·Design Spec | · 生成设计文档 | 30 | 40 |
| ·Design Review | · 设计复审 (和同事审核设计文档) | 30 | 20 |
| ·Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 30 |
| ·Design | · 具体设计 | 120 | 160 |
| · Coding | · 具体编码 | 150 | 180 |
| ·Code Review | · 代码复审 | 40 | 60 |
| ·Test | · 测试(自我测试,修改代码,提交修改) | 150 | 200 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 60 | 90 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 40 |
| 合计 | 750 | 970 |
对结对的小伙伴做出评价
我的结对小伙伴徐雯编程基础很好,所以驾驶员是由她担当的,主要代码的编写都是由她完成,而我基本是监督、修改她的代码。徐雯是一个对打代码严谨、创新、精益求精的人,每一个类每一个方法都分的清晰明白,在和她结对的过程中,我也学会了很多编代码的思路。我非常高兴能和徐雯结对编程~