221.最大正方形

解法1（暴力解法）

思路

• 遍历数组，依次以每一个点作为正方形的左上角
• 计算所能构成正方形的最大边长
• 在最大正方形的范围内，边长从小到大增大。边长每增加1，则新增一行一列，判断新增的点是否为 '1'，maxSide保存符合要求的边的值。
• 注意细节处理

代码

 
/*
 *暴力解法
 *4ms
 */
public int maximalSquare2(char[][] matrix){
        int maxSide=0;
        if(matrix==null||matrix.length==0||matrix[0].length==0) return maxSide;
        int r=matrix.length,c=matrix[0].length;
        for(int i=0;i<r;i++){
            for(int j=0;j<c;j++){
                if(matrix[i][j]=='1'){
                    //一个值为1的点 可以构成一个边长为1的正方形
                    maxSide=Math.max(maxSide, 1);
                    //以当前点  作为 正方形的左上角顶点，计算能构成正方形的最大边长
                    int curMaxSide=Math.min(r-i, c-j);
                    for(int k=1;k<curMaxSide;k++){
                        boolean flag=true;
                        //判断正方形的右下角顶点是否为1  (对角线上)
                        if(matrix[i+k][j+k]=='0'){
                            break;
                        }
                        //新增一行一列 判断多出来的点是否为 '1' 不包含右下角顶点
                        for(int m=0;m<k;m++){
                            if(matrix[i+k][j+m]=='0'||matrix[i+m][j+k]=='0'){
                                flag=false;
                                break;
                            }
                        }
                        if(flag){
                            maxSide=Math.max(maxSide, k+1);
                        }else{
                            break;
                        }
                    }
                }
            }
        }
        return maxSide*maxSide;
    }

解法2(动态规划)

官方思路

• 通过动态规划降低时间复杂度，用dp(i,j)表示以（i,j）为右下角，且只包含1的正方形的边长的最大值。

• 如何计算dp的值？

  • 如果该位置的值是0，则dp(i,j)=0

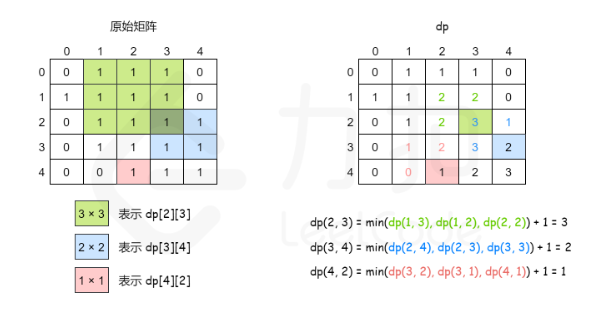
  • 如果该位置的值为1，则dp(i,j)的值由其上方，左方和左上方的三个相邻位置的dp值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加+1

    dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1

    推导过程链接: 1277.统计全为1的正方形子矩阵

  • 此外 需考虑边界条件。如果i和j中至少有一个为0，则以位置（i，j）为右下角的最大正方形的边长只能为1,即dp(i,j)=1

代码

 /**
     * 6ms 动态规划
     * @param matrix
     * @return
     */
    public int maximalSquare3(char[][] matrix){
        int maxSide=0;
        if(matrix==null||matrix.length==0||matrix[0].length==0) return maxSide;
        int rows=matrix.length,columns=matrix[0].length;
        int[][] dp=new int[rows][columns];
        for(int i=0;i<rows;i++){
            for(int j=0;j<columns;j++){
                if(matrix[i][j]=='1'){
                    if(i==0||j==0){
                        dp[i][j]=1;
                    }else{
                        dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]), dp[i-1][j-1])+1;
                    }
                    maxSide=Math.max(maxSide, dp[i][j]);
                }
            }
        }
        return maxSide*maxSide;
    }