最近写了一些关于字典树的题目,这里做个简单的整理。
字典树,又叫单词查找树,顾名思义就是查单词的(不仅仅o),和词典一样。不同的是词典是用纸做的,而字典树是用树形结构构建的。
她用来快速检索你要的内容,对于统计和大量字符串的排序是很好用的。她的好处就是让你尽可能的减少那么过分多且没必要的比较,提供高效的检索。Trie的核心是空间换时间,没错,开销不少,这可能是个缺点吧。
首先,她的根结点仅仅是个根结点,什么都没有,可以看做是一本词典的封面,想要查询单词,先得打开封面(进入根结点)。
进入根结点后立马会看到a-z共26个结点,没错,这是给你选择的地方,根据你要查询的单词的首字母选择对应的结点(每个结点对应唯一一个字符),进入即可。
重复上述步骤,就可以得到你想要的结果(你要查询的字符串就是路径到叶子结点的总和)。
查找过程,你不会发现有重复的字母,也就是你不会在两条不同的路径上找到同一个字符串,每个节点的所有子节点包含的字符都不相同。这就是Trie的三个特性。
她的存放就如这样:
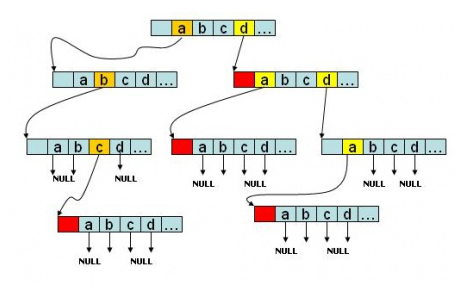
当然,最上面的上面还有个根结点。最左边就是我查找abc这个字符串的过程,中间一个对应为da,最右边为dda。很明显,这个Trie只有三个字符串,只要你想,空间够大,你完全可以存放一本英文大词典~~~。(开销不少哈哈哈)
好了,聊聊怎么建树吧。
Trie树一般有建立和查询两个基本操作,删除的操作挺少见的(目前还没见过,可能是见识短吧~)。
建树的过程其实很简单,首先,树的每个结点并不是简简单单的字符,而是包含了26个字符,还有一个指针域,指向下一个字符。

1 struct node 2 { 3 int cnt; 4 char c[26];//结点所对应的字符 5 struct node *next[26]; 6 node () 7 { 8 cnt = 0; 9 memset(next,0,sizeof(next)); 10 } 11 }; 12 node * root = NULL;//根结点初始为NULL
其中变量cnt有个作用,即表明让前结点是否为一个字符串的最后一个结点。不然这样一棵Trie树会无限循环建立下去,一个单词总有个长度的。

1 void BuildTrie(char *s,char *temp) 2 { 3 node *p = root;//p指向根结点 4 node *tmp = NULL; 5 int l = strlen(s);//计算创建单词的长度 6 for(int i = 0;i < l ;i ++)//对每个字符处理 7 { 8 if(p->next[s[i]-'a'] == NULL)//如果p结点的指针对应的单词的字符为空,就要创建她 9 {//如 我要创建字符串为 china,而我发现当前只有个c,后面应该有的h却是空的,所以建立h 10 tmp = new node;//tmp为空 11 p->next[s[i]-'a'] = tmp;//p:目前的结点 如c,那么她的下一个字符指针指向tmp) 12 //tmp所对应的 字符就是h,为什么呢? 因为这个 “s[i]-'a'”,h-‘a’所对应的数组下标就是h 13 } 14 p = p->next[s[i]-'a'];//p更新为当前的结点即转移到h结点,继续上述过程 15 } 16 p->cnt = 1;//到了最后一个a结点,将a的cnt置为1,表示这个单词结束了,按照这个路径下来查到的一定是china 17 strcpy(p->c,temp);//最后的叶子结点可以放你想查询到的最终结果,即你找到china所应该的信息 18 //如翻译 ,如果你找了china,那么我在最后放一个“中国” 19 }
在知道了怎么建树后,查询其实也差不多了,和建树很相似的过程。

1 void Query(char *s) 2 { 3 node *p = root; 4 int l = strlen(s); 5 for(int i = 0 ;i< l ;i++) 6 { 7 if(p->next[s[i]-'a'] == NULL) 8 { 9 printf("404 "); 10 return ; 11 } 12 p = p->next[s[i]-'a']; 13 } 14 printf("%s ",p->c);//打印最终查询结果 15 return ; 16 }
这里要说一句,这里的查询时间和树没多大关系,而是和所查找单词的长度有关(好像说了句废话-,-)。因为她有个亲戚叫二叉查找树,她也可以用来查单词,但是查找时间和树中结点数有关,复杂度为O(lon2n),而对于一个不是很长很长的字符串s来说,Trie只要比较strlen(s)次,而二叉查找树要比较log2(26^strlen(s))次,效率呢自己带个数看看就一目了然了~
当然,Trie不经可以用来检索单词,还能统计词频率(加计数),计算最长公共前缀,当然还能用来A题
