在现实生活中,我们知道给出一些亲戚关系的信息,如A和B是亲戚,B和C也是亲戚,那么我们可以得出A和C也是亲戚。这是so easy 的的。我们看看下面的例子:
输入部分:给定N个人,M对数字,这些数字对表示某两个人是亲戚。接下来给定一个Q,表示Q对提问,求这些提问对中二者是否为亲戚
10 7 //N=10,M =7
2 4
5 7
1 3
8 9
1 2
5 6
2 3
3//Q
3 4
7 10
8 9
这类问题,数据量多的时候,我们可以采用集合的方式求解
关系 等价类/集合
10个人 {1} {2} {3} {4} {5} {6} {7} {8} {9} {10}
(2,4) 是亲戚,合并集合 {1} {2,4} {3} {5} {6} {7} {8} {9} {10}
(5,7) ... {1} {2,4} {3} {5,7} {6} {8} {9} {10}
(1,3) ... {1,3} {2,4} {5,7} {6} {8} {9} {10}
(8,9) ... {1,3} {2,4} {5,7} {6} {8,9} {10}
(1,2) ... {1,2,3,4} {5,7} {6} {8,9} {10}
(5,6) ... {1,2,3,4} {5,6,7} {8,9} {10}
(2,3) ... {1,2,3,4} {5,6,7} {8,9} {10}
最后根据提问的要求,判断是否在一个集合就可以判断是否为亲戚了。
实现并查集的算法实现(O(log2n)):
 View Code
View Code

1 struct node 2 { 3 /* data */ 4 int date;//结点对应的下标 5 int parent;//双亲结点 6 int rank;//结点对应秩(并查集树的深度) 7 int relation; //与父节点的关系 8 }; 9 10 class DisJoinSet 11 { 12 protected: 13 int n;//元素个数 14 node *tree;//并查集元素数组 15 public: 16 DisJoinSet(int n ); 17 ~DisJoinSet(); 18 void Init(); 19 int Find(int x);// 查找x的代表元素(根),查找的同时进行路径压缩 20 void Union(int x,int y); 21 int GetAnswer();// 合并x和y 22 };
一般我们用结构题存放每个元素,包括编号和rank,父亲结点,relation(与上层结点的关系(不少题目需要这样的设置))

1 DisJoinSet::DisJoinSet(int n) 2 { 3 this->n = n ; 4 tree = new node [n+1]; 5 Init(); 6 } 7 8 void DisJoinSet ::Init() 9 { 10 for(int i = 1 ;i <=n; i++)//顶点编号 0~n-1 或 1 ~ n都 行 11 { 12 tree[i].parent = i;//双亲初始化指向自已 13 tree[i].rank = 0;//秩初始化为0 14 tree[i].date = i;//编号 15 tree[i].relation = 0; //i自己是一类,它的父节点此时就是它自己,属于同一类 16 } 17 } 18 19 DisJoinSet::~DisJoinSet() 20 { 21 delete []tree; 22 }
初始化过程,首先每个元素都是单独一个集合,所以父亲结点指向自己本身。

1 int DisJoinSet::Find(int x)//查找x的代表元素(根),查找的同时进行路径压缩 2 { 3 int temp = tree[x].parent;// 将x父节点的下标存入temp 4 if( x != tree[x].parent)//若双亲不是自已 5 { 6 tree[x].parent = Find(tree[x].parent);//递归在双亲中找x 7 return tree[x].parent;// 返回根节点下标 8 } 9 return x;//若双亲是自已,返回x 10 }
这里我们提到一个路径压缩的问题。实际上是这样的。在查找到根结点的时候,我们把属于这个根所在集合的所有元素都直接挂在根的下边。即构成一个2层高,很宽的树型。像这样
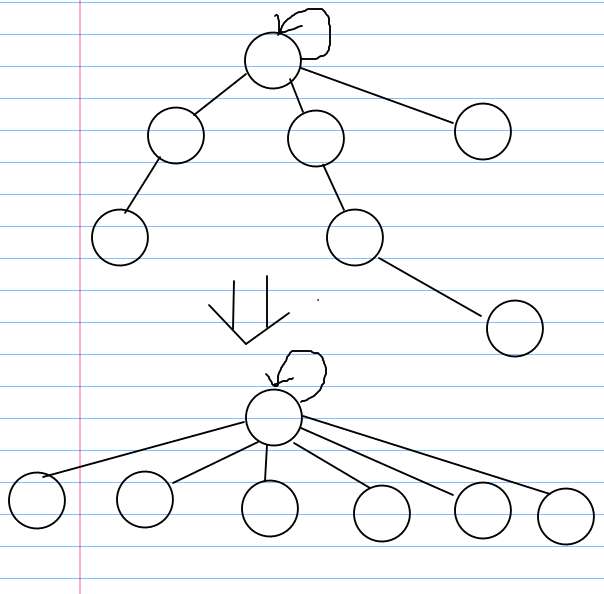
在对每一个元素进行查找所在集合(根)的时候,都递归的将其父亲结点改为根结点。这样做的目的是为了溯源方便。根就比如一个大学,那么多的大学生所对应的大学肯定不一样。如果第一种情况,别人问你的根(所在集合/大学)是什么,那么你就得问你的父亲结点(辅导员),辅导员要问他的父亲结点(系主任),系主任要问他的父亲结点(院长),院长则要问校长,校长再一次次反馈下来你的学校是什么,就很浪费时间。而路径压缩过的好处就是,每个学生都直接挂在学校下面,对一次Find,都能很快反馈学校信息。这样是很方便的。

1 // 合并x和y 2 void DisJoinSet::Union(int x, int y) 3 { 4 int rootx = Find(x); // 找到下标为x的元素的根节点下标rootx 5 int rooty = Find(y); // 找到下标为y的元素的根节点下标rooty 6 if (rootx == rooty) // 已合并,还搞个毛,直接返回 7 { 8 return; 9 } 10 11 if (tree[rootx].rank > tree[rooty].rank) //rooty结点的秩(深度)小于rootx结点的秩 12 { 13 tree[rooty].parent = rootx; //将rooty连到rootx结点上,rootx作为rooty的孩子结点 14 } 15 else //rooty结点的秩大于等于rootx结点的秩 16 { 17 tree[rootx].parent = rooty; //将rootx连到rooty结点上,rooty作为rootx的孩子结点 18 if (tree[rootx].rank == tree[rooty].rank) //rootx和rooty结点的秩(深度)相同 19 { 20 tree[rooty].rank++; //rooty结点的秩增1 21 } 22 } 23 }
这段合并操作,如果二者所在集合(rootx,rooty)相同,说明已经是一类了,直接返回。
否则,进行一个判断,判断两个即将合并的集合哪个的秩小些, 将小的那个集合的根挂到大的集合的根下边。稍微思考下,如果反过来,那么原来在秩大的那个集合的叶子Find时又多了一层递归,显然效率低了些。
这只是并查集的基本框架,对于不同题目的不同要求,还要灵活的处理才行。
