【LeetCode】【矩阵旋转】Rotate Image

描述

You are given an n x n 2D matrix representing an image.

Rotate the image by 90 degrees (clockwise).

Note:

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

Given input matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

rotate the input matrix in-place such that it becomes:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

Example 2:

Given input matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

rotate the input matrix in-place such that it becomes:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

思路：移位法

将矩阵的的边框连线

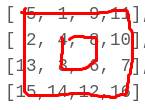
如果矩阵的宽度和高度都为n，那么一共有n/2个连线框，这些连线框位移形成旋转矩阵，如下图 

 按顺时针位移，依次遍历连线上的点就行。

这里为了不增加额外的空间消耗，不创建新的矩阵，我们用一个temp变量，存放临时的待替换元素，如果要顺时针替换，则需要两个临时变量还要不断更新，所以我们采用逆时针旋转替换，这样只需要在开始的时候加入一个temp变量即可。

然后遍历的时候令i为旋转的圈数，j为直线上遍历的序号。使得j=i，j增大到n-1-i，然后根据四个点的序号关联完成转移。

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        int count = n/2,temp = 0;
        for(int i = 0;i < count;++i){
            for(int j = i;j<n-i-1;++j){
                temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};