前序
由于我个人问题对本题做一个题解记录一下
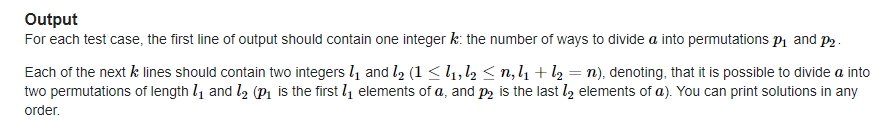
题目在输出的时候做出了一个 and 长度范围的限定,这对我第一的代码中的 for 循环范围产生了一定设定上的偏差,从左端上看 and 是必定满足 ,由于这个条件所以左端是不可能达到 这个位置的所以范围应该是
题目链接
题目类型
思维、模拟
题意简述
给你一段长度为 的序列,要求你将该序列分为两个部分,分别为序列 和 ,长度分别为 和 ,这两个序列分别满足满足序列中的元素可以通过排列变成连续序列,且元素刚好只出现一次,问能分成多少种,输出每种 和 的值。
题解
first(TLE-3)
我原先想到的是set解法,将所有的长度枚举一遍,存储在 set 容器中,因为set容器中去重有序的性质,如果最后一个元素与长度不相符,就说明有重复出现是不符合的,或者是元素不是连续的。
时间复杂度
- 每个长度需要枚举一遍也就是O(n)
- 每个次分成的两个序列都需要插入set也就是 O(n)
- 每次set中count查询出现次数都是 o(log n),个人觉得卡的就是查询
- 每次还要对set进行清除,
set.clear()底层的实现就是通过earse删除,时间复杂度O(n)
最后总的时间复杂度为O(nlogn)
代码
这里给出代码只是一个思路的参考,是TLE的,要注意,应该是可以用 unordered_map 去进行一个优化,但我是懒了
const int maxn = 2e5+50;
set<int> ap;
int a[maxn];
vector<PII> ans;
int main(){
int t;
for(scanf("%d",&t);t;t--){
ans.clear();
int n; RD(n);
REP(i, n) RD(a[i]);
for(int len = 1; len <= n - 1; len++){
ap.clear();
bool judge = true;
//cout << "len :" << len << '
';
for(int i = 0; i < len; ++i){
ap.insert(a[i]);
}
int tmp;
tmp = *(--(ap.end()));
if (ap.size() != len || ap.size() != tmp) continue;
ap.clear();
for(int i = len; i < n; i++){
ap.insert(a[i]);
}
tmp = *(--(ap.end()));
if (ap.size() != n - len || ap.size() != tmp) continue;
ans.PB(MP(len,n - len));
}
if (ans.size() == 0) {
cout << 0 << '
';
}
else{
cout << ans.size() << '
';
for(PII v: ans){
cout << v.fi << " " << v.se << '
';
}
}
}
}
second
官方解答

设ma为a中所有元素的最大值。如果可以将a序列分解为两个排列 and ,那么ma必须与和中最大的那一个值相等。
所以最多有两种情况:
我们可以分别检查这两种情况,时间复杂度为O(n)。
代码
写法一(TLE)
//判断是否访问过
const int MAXN = 2e5+50;
int used[MAXN];
bool judge_used(int a[], int n){
REP(i, n+1) used[i] = 0;
REP(i, n) used[a[i]] = 1;
FOR_1(i, 1, n) if (!used[i]){return false;}
return true;
}
vector<PII> ans;
const int maxn = 2e5+50;
int a[maxn];
int main(){
int t;
for(scanf("%d", &t); t; t--){
ans.clear();
int n, ma = 0; RD(n);
REP(i, n) { RD(a[i]); ma = max(ma, a[i]);}
for(int len1 = 1; len1 <= n - 1; ++len1){
if (judge_used(a, len1) && judge_used(a + len1, n - len1)){
if (ma == len1 || ma == n - len1) ans.PB(MP(len1, n - len1));
}
}
cout << ans.size() << '
';
for(PII v : ans){
cout << v.fi << " " << v.se << '
';
}
}
}
超时的点主要是枚举所有长度的时候超时,所以应该直接判断去做,这里枚举长度所造成的时间复杂度是O()超时是必然的
正确代码
//判断是否访问过
const int MAXN = 2e5+50;
int a[MAXN];
int used[MAXN];
int ans[MAXN][2];
int ans_cnt;
bool judge_used(int a[], int n){
REP(i, n+1) used[i] = 0;
REP(i, n) used[a[i]] = 1;
FOR_1(i, 1, n) if (!used[i]){return false;}
return true;
}
bool judge(int len1, int n){
return judge_used(a, len1) && judge_used(a + len1, n - len1);
}
int main(){
int t;
for(scanf("%d", &t); t; t--){
ans_cnt = 0;
int n, ma = 0; RD(n);
REP(i, n) { RD(a[i]); ma = max(ma, a[i]);}
if(judge(n - ma,n)) {
ans[ans_cnt][0] = n - ma;
ans[ans_cnt++][1] = ma;
}
if(ma * 2 != n && judge(ma,n)) {
ans[ans_cnt][0] = ma;
ans[ans_cnt++][1] = n - ma;
}
printf("%d
", ans_cnt);
for(int i = 0; i < ans_cnt; i++) {
printf("%d %d
", ans[i][0], ans[i][1]);
}
}
}