一、哈希函数
1.1 什么是哈希函数
哈希函数(Hash Function),也称为散列函数。是将一个大文件映射成一个小串字符。与指纹一样,就是以较短的信息来保证文件的唯一性的标志,这种标志与文件的每一个字节都相关,而且难以找到逆向规律。
举个例子:
服务器存了10个文本文件,你现在想判断一个新的文本文件和那10个文件有没有一个是一样的。你不可能去比对每个文本里面的每个字节,很有可能,两个文本文件都是5000个字节,但是只有最后一位有所不同,但这样的,你前面4999位的比较就是毫无意义。那一个解决办法,就是在存储那10个文本文件的时候,都将每个文件映射成一个hash字符串。服务器只需要存储10个hash字符串,在判断的时候,只需要判断新的这个文本文件的hash值是否和那10个文件的hash值一致,那就可以解决这个问题了。
简单点说,hash就是将任意长度的消息压缩成某一固定长度的消息摘要的函数。
由于文件是无限的,而映射后的字符串能表示的位数是有限的。因此可能会存在不同的key对应相同的Hash值。这就是存在碰撞的可能。
Hash算法是不可逆的,即不同通过Hash值逆向推出key的值。
1.2 哈希函数的性质
对于经典哈希函数来说,它具有以下5点性质:
- 输入域无穷大
- 输出域有穷尽
- 输入一样,输出肯定一样
- 当输入不一样,输出也可能一样(哈希碰撞)
- 不同输入会均匀分布在输出域上(哈希函数的离散性)
例如输入域是0-98这99个数字,而我们使用的哈希函数的输出域为0,1,2,当我们将0-98这99个数字通过该哈希函数,得到的返回值,0,1,2数量都会接近33个,不会出现某个返回值数量特别多,而某个返回值特别少。
注意:对于哈希函数来说,有规律的输入并不能得到有规律的输入,例如十个1Mb的字符串,只有最后1byte的内容不一样,在经过哈希函数后得到的返回值会千差万别,而不会有规律,所以它可以来打乱输入规律。
通常哈希函数的输出域都很大,例如常见的MD5算法,它的输出域是0到264-1,但是往往我们都会将哈希函数的返回值模上一个较小的数m,让哈希函数的输出域缩减为0到m-1,并且模完后的0到m-1这个域上也是均匀分布的。
1.3 如何快速生成多个哈希函数
假如你急需要1000个哈希函数,并且这1000个哈希函数都要求相互独立,不能有相关性。这时,错误的方法是去在网上寻找1000个哈希函数。我们可以通过一个哈希函数来生成这样的1000个独立的哈希函数。
假如,你有一个哈希函数f,它的输出域是264,也就是16字节的字符串,每个位置上是16进制的数字0-9,a-f。
我们将这16字节的输出域分为两半,高八位和低八位是相互独立的(这16位都相互独立)。这样,我们将高八位作为新的哈希函数f1的输出域,低八位作为新的哈希函数f2的输出域,得到两个新的哈希函数,它们之间相互独立。
故此可以通过以下算式得到1000个哈希函数:
f1+1*f2=f3 f1+2*f2=f4 f1+3*f2=f5 ……
1.4 哈希函数在大数据中的应用
需求:我们有一个10TB的大文件存在分布式文件系统上,存的是100亿行字符串,并且字符串无序排列,现在我们要统计该文件中重复的字符串。
整体思路:利用哈希函数分流,以及哈希表的性质:相同输入导致相同输出,不同输入均匀分布。
假设,我们可以调用100台机器来计算该文件。
那么,现在我们需要怎样通过哈希函数来统计重复字符串呢。
首先,我们需要将这一百台机器分别从0-99标好号,然后我们在分布式文件系统中一行行读取文件(多台机器并行读取),通过哈希函数计算hashcode,将计算出的hashcode模以100,根据模出来的值,将该行存入对应的机器中。
根据哈希函数的性质,我们很容易看出,相同的字符串会存入相同的机器中。
然后我们就能并行100台机器,每台机器各自统计有哪些重复的字符串,这样就能大大加加快统计的速度。
如果还嫌单个机器处理的数据过大,可以把机器里的文件再通过哈希函数按照同样的方法把它分成小文件,然后在一台机器中并行多个进程,处理数据。
注意:这10TB文件并不是均分成100GB,分给100台机器,而是将这10TB文件中不同字符串的种类,均分到100台机器中。
二、哈希表
我们知道,哈希表中存入的数据是key,value类型的,哈希表能够put(key,value),同样也能get(key,value)或者remove(key,value)。当我们需要向哈希表中put(插入记录)时,我们将key拿出,通过哈希函数计算hashcode。假设我们预先留下的空间大小为17,我们就需要将通过key计算出的hashcode模以17,得到0-16之间的任意整数,然后我们将记录挂在相应位置的下面(包括key,value)。
假如我们要将(zhangsan,20)这样一条记录插入哈希表中,首先我们通过哈希函数,计算出zhangsan的hashcode,然后模以17,假如我们得到的值是3,哈希表会先去检查6位置下是否存在数据。如果有,检查该节点中的key是否等于zhangsan,如果等于,则将该节点中的value替换为20;如果不等于,则在链表的最后新添加一个节点,保存我们的记录。
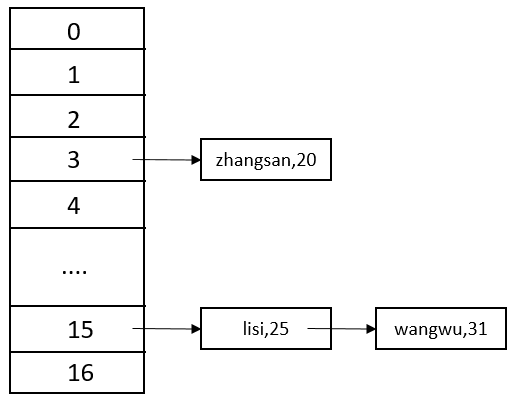
由于哈希函数的性质,得到的hashcode会均匀分布在输出域上,所以模上17之后,即便不同的输入,也会在0到16上均匀分布。这就意味着我们哈希表每个位置下面的链表长度相近。
在实际哈希表应用中,它的查询速度近乎O(1),这是因为通过key计算hashcode的时间是常数项时间,而数组寻址的时间也是常数时间。
怎么保证哈希表的效率为O(1)呢?这里的哈希表长度只有17,如果N很大的话,每条链的长度就是N/17,那就是O(N)的复杂度了,根本就做不到O(1)啊?
所以,当样本量逼近一个数量,比如说我发现某条链的长度已经到3了,那我可以认为其它链的长度也差不多到3了,如果接下来还是这样操作,效率可能就不行了,此时就会经历哈希表的扩容。
假设我们将哈希表的范围由原来的17扩到104,扩容的时候就是把每一个数据都拿出来,重新用哈希函数算完之后,再模上104,然后重新分配在新表的哪一个位置上,这样就完成了哈希表的扩容。
你可能会说,扩容代价不用计算吗?为什么能够做到O(1)呢?
一方面,样本量为N时,如果每次扩容过程中,都让原来的长度增加一倍,扩到N需要扩logN次;如果说每次扩容时长度增加5倍,那么扩容的平均复杂度就是log5N,所以复杂度可以压得很低,而且,扩容这个代价不是时刻都发生的,虽然某一次扩容会消耗一些代价,但问题在于你是成倍扩容的,扩容一次之后可能很久都不用扩容了,所以平均下来这个复杂度就非常低了。
你又会有疑问,这也不足以说是O(1)吧?
实际在使用过程中,还可以离线扩容。比如说这个哈希表的长度是1000,在用的时候发现某条链上的长度为5了,长度为5并不影响使用,增删改查还是O(1),只是再往上加的时候它的效率快不行了,但是你在get或put时还让你使用原来的结构,于此同时,我在后台给你分配一个更大的区域,比如容量为3000。一个数据经过哈希函数算完后,拿到新结构里放,如果用户有put行为,就同步往新老结构上塞,用户使用get时,从老结构上拿,也就是说不让使用者等待。当后台彻底扩容完成后,用户再用的时候,就把请求切换到新的结构上,然后把老结构销毁,这就是离线扩容。
因为有这么多的优化技巧,所以我们说哈希表的增删改查是O(1)的。
三、设计RandomPool结构
【题目】
设计一种结构,在该结构中有如下三个功能:insert(key):将某个key加入到该结构,做到不重复加入。delete(key):将原本在结构中的某个key移除。 getRandom():等概率随机返回结构中的任何一个key。
要求:Insert、delete和getRandom方法的时间复杂度都是O(1)
【分析】
这个题的结构和哈希表的结构很像,不同的是哈希表是get(key,value),而这题没有value,只有key,但有getRandom()这个函数。
如果用一张哈希表不能做到等概率随机返回任何一个key,哈希表的结构是,表中的每个位置上都挂一些链,如果样本量很少,必然会出现某一个位置上有数据,其它位置没数据的情况,此时又不能遍历,因为遍历就不是O(1)了;样本量很多的时候,虽然说会均匀分布, 每个位置链的长度几乎差不多,但也不是严格一样,所以只用一张哈希表是做不到严格等概率返回一个key的。
准备两个哈希表,假设A~Z依次进入,哈希表的结构就是:

如果要等概率随机返回一个,可以使用Math.random() * size 随机产生[0,25)中等概率的一个数,随机出哪个数字,就在map2里把该数字对应的字符串返回,这就能做到绝对等概率。
以上是insert(key)和getRandom()的行为。
delete(key)又该怎么做呢?
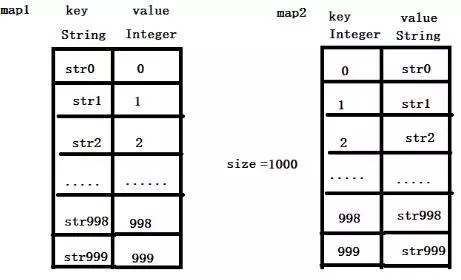
如果直接在map1和map2中进行删除操作的话,会产生一个个的“洞”,如果0~999这1000个数中,执行了999个删除操作,那么0~999中产生了999个“洞”,只有一个位置上有数据,此时,如果getRandom()的话就会非常慢,这样就不能保证O(1)的时间复杂度。
正确的做法应该是:假设删除了map1中str2上的数据,map2对应的数据也会同步删除,然后把str999放到str2的位置上,再让str2对应的字符串改为999,然后删掉最后一条记录,size变为999。
即产生“洞”的时候,拿最后一个数据“填”这个“洞”,再把最后几个记录删掉,这样就能保证size的index区域还是连续的,此时getRandom()产生的随机数的位置就不会为空了。
注意:value上的0~999这个顺序并不是有序的,因为map本身就是乱序的,我们也不需要value是有序的,我们只要保证map上不存在“洞”,每条记录都是连续的,这样在getRandom()时就不会找不到数。
public class RandomPool { public static class Pool<K> { private HashMap<K, Integer> keyIndexMap; private HashMap<Integer, K> indexKeyMap; private int size; public Pool() { this.keyIndexMap = new HashMap<>(); this.indexKeyMap = new HashMap<>(); this.size = 0; } public void insert(K key) { if (!this.keyIndexMap.containsKey(key)) { this.keyIndexMap.put(key, this.size); this.indexKeyMap.put(this.size++, key); } } public void delete(K key) { if (this.keyIndexMap.containsKey(key)) { int deleteIndex = this.keyIndexMap.get(key); int lastIndex = --this.size; K lastKey = this.indexKeyMap.get(lastIndex); //把最后一条记录"填"到要删除的位置 this.keyIndexMap.put(lastKey, deleteIndex); this.indexKeyMap.put(deleteIndex, lastKey); this.keyIndexMap.remove(key); this.indexKeyMap.remove(lastIndex); } } public K getRandom() { if (this.size == 0) { return null; } //0 ~ size -1 int random = (int) (Math.random() * this.size); return this.indexKeyMap.get(random); } } public static void main(String[] args) { Pool<String> pool = new Pool<>(); pool.insert("A"); pool.insert("B"); pool.insert("C"); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); } }
四、认识布隆过滤器
4.1 前言
在日常生活中,包括在设计计算机软件时,我们经常要判断一个元素是否在一个集合中。比如在字处理软件中,需要检查一个英语单词是否拼写正确(也就是要判断它是否在已知的字典中);在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上;在网络爬虫里,一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中,遇到一个新元素时,将它和集合中的元素直接比较即可。一般来讲,计算机中的集合是用哈希表(hash table)来存储的。它的好处是快速准确,缺点是费存储空间。当集合比较小时,这个问题不显著,但是当集合巨大时,哈希表存储效率低的问题就显现出来了。比如说,一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件(email)提供商,总是需要过滤来自发送垃圾邮件的人(spamer)的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址,全世界少说也有几十亿个发垃圾邮件的地址,将他们都存起来则需要大量的网络服务器。如果用哈希表,每存储一亿个 email 地址, 就需要 1.6GB 的内存。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机,一般服务器是无法存储的。接下来,我们介绍一种称作布隆过滤器的数学工具,它只需要哈希表 1/8 到 1/4 的大小就能解决同样的问题。
4.2 什么是布隆过滤器
布隆过滤器 (Bloom Filter)是由Burton Howard Bloom于1970年提出,它是一种space efficient的概率型数据结构,用于判断一个元素是否在集合中。在垃圾邮件过滤的黑白名单方法、爬虫(Crawler)的网址判重模块中等等经常被用到。哈希表也能用于判断元素是否在集合中,但是布隆过滤器只需要哈希表的1/8或1/4的空间复杂度就能完成同样的问题。布隆过滤器可以插入元素,但不可以删除已有元素。其中的元素越多,false positive rate(误报率)越大,但是false negative (漏报)是不可能的。即布隆过滤器可以用来告诉你 “某样东西一定不存在或者可能存在”。
4.3 算法思想
Bloom-Filter算法的核心思想就是利用多个不同的Hash函数来解决“冲突”。
计算某元素x是否在一个集合中,首先能想到的方法就是将所有的已知元素保存起来构成一个集合R,然后用元素x跟这些R中的元素一一比较来判断是否存在于集合R中;我们可以采用链表等数据结构来实现。但是,随着集合R中元素的增加,其占用的内存将越来越大。试想,如果有几千万个不同网页需要下载,所需的内存将足以占用掉整个进程的内存地址空间。即使用MD5,UUID这些方法将URL转成固定的短小的字符串,内存占用也是相当巨大的。
于是,我们会想到用Hash table的数据结构,运用一个足够好的Hash函数将一个URL映射到二进制位数组(位图数组)中的某一位。如果该位已经被置为1,那么表示该URL已经存在。
但是Hash存在一个冲突(碰撞)的问题,用同一个Hash得到的两个URL的值有可能相同。为了减少冲突,我们可以多引入几个Hash,如果通过其中的一个Hash值我们得出某元素不在集合中,那么该元素肯定不在集合中。只有在所有的Hash函数告诉我们该元素在集合中时,才能确定该元素存在于集合中。这便是Bloom-Filter的基本思想。
4.4 实现过程
首先需要准备:一个位数组、K个独立hash函数
1)位数组:
假设Bloom Filter使用一个m比特的数组来保存信息,初始状态时,Bloom Filter是一个包含m位的位数组,每一位都置为0,即BF整个数组的元素都设置为0。
![]()
2)添加元素,k个独立hash函数
为了表达S={x1, x2,…,xn}这样一个n个元素的集合,Bloom Filter使用k个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到{1,…,m}的范围中。2)添加元素,k个独立hash函数
当我们往Bloom Filter中增加任意一个元素x时候,我们使用k个哈希函数得到k个哈希值(可以对应数组下标),然后将数组中对应的比特位设置为1。即第i个哈希函数映射的位置hashi(x)就会被置为1(1≤i≤k)。
注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位,即第二个“1“处)。

3)判断元素是否存在集合
在判断y是否属于这个集合时,我们只需要对y使用k个哈希函数得到k个哈希值,如果所有hashi(y)的位置都是1(1≤i≤k),即k个位置都被设置为1了,那么我们就认为y是集合中的元素,否则就认为y不是集合中的元素。下图中y1就不是集合中的元素(因为y1有一处指向了“0”位)。y2或者属于这个集合,或者刚好是一个false positive。

很显然这个判断并不能保证查找的结果是100%正确的。
接下来再举个具体的例子来解释上面过程:
准备一个布隆过滤器( bit 数组),长这样:

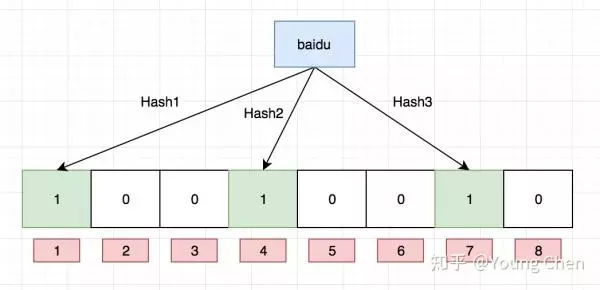
Ok,我们现在再存一个值 “tencent”,如果哈希函数返回 3、4、8 的话,图继续变为:

解析一下为什么布隆过滤器不能删除已有元素,例如上图中的 bit 位 4 被两个值共同覆盖的话,一旦你删除其中一个值例如 “tencent” 而将其置位 0,那么下次判断另一个值例如 “baidu” 是否存在的话,会直接返回 false,而实际上你并没有删除它。
4.5 确定哈希函数个数和布隆过滤器长度
很显然,过小的布隆过滤器很快所有的 bit 位均为 1,那么查询任何值都会返回“可能存在”,起不到过滤的目的了。布隆过滤器的长度会直接影响误报率,布隆过滤器越长其误报率越小。
另外,哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置位 1 的速度越快,且布隆过滤器的效率越低;但是如果太少的话,那我们的误报率会变高。
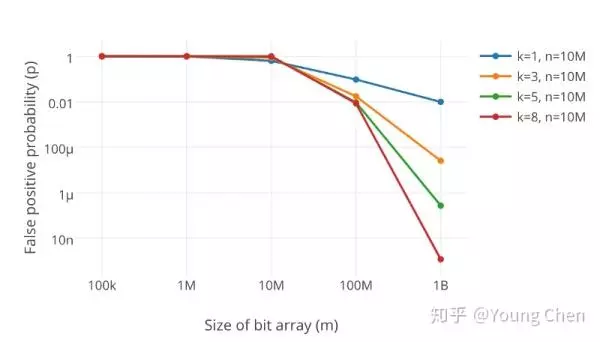
k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率。
接下来介绍设计和应用布隆过滤器的方法:
实际应用时首先要先由用户决定要插入的元素数n和希望的误差率P。这也是一个设计完整的布隆过滤器需要用户输入的仅有的两个参数,之后的所有参数将由系统计算,并由此建立布隆过滤器。
系统首先要计算需要的内存大小m bits:(如果m算出来是小数的话,向上取整如果m算出来是小数的话,向上取整)
![]()
再由m,n得到哈希函数的个数:
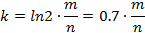
当m和k向上取整确定了后,真实的失误率是:
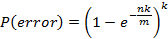
五、认识一致性哈希
在了解一致性哈希算法之前,最好先了解一下缓存中的一个应用场景,了解了这个应用场景之后,再来理解一致性哈希算法,就容易多了,也更能体现出一致性哈希算法的优点,那么,我们先来描述一下这个经典的分布式缓存的应用场景。
5.1 场景描述
假设,我们有三台缓存服务器,用于缓存图片,我们为这三台缓存服务器编号为0号、1号、2号,现在,有3万张图片需要缓存,我们希望这些图片被均匀的缓存到这3台服务器上,以便它们能够分摊缓存的压力。也就是说,我们希望每台服务器能够缓存1万张左右的图片,那么,我们应该怎样做呢?如果我们没有任何规律的将3万张图片平均的缓存在3台服务器上,可以满足我们的要求吗?可以!但是如果这样做,当我们需要访问某个缓存项时,则需要遍历3台缓存服务器,从3万个缓存项中找到我们需要访问的缓存,遍历的过程效率太低,时间太长,当我们找到需要访问的缓存项时,时长可能是不能被接受的,也就失去了缓存的意义,缓存的目的就是提高速度,改善用户体验,减轻后端服务器压力,如果每次访问一个缓存项都需要遍历所有缓存服务器的所有缓存项,想想就觉得很累,那么,我们该怎么办呢?原始的做法是对缓存项的键进行哈希,将hash后的结果对缓存服务器的数量进行取模操作,通过取模后的结果,决定缓存项将会缓存在哪一台服务器上,这样说可能不太容易理解,我们举例说明,仍然以刚才描述的场景为例,假设我们使用图片名称作为访问图片的key,假设图片名称是不重复的,那么,我们可以使用如下公式,计算出图片应该存放在哪台服务器上。
hash(图片名称)% N
因为图片的名称是不重复的,所以,当我们对同一个图片名称做相同的哈希计算时,得出的结果应该是不变的,如果我们有3台服务器,使用哈希后的结果对3求余,那么余数一定是0、1或者2,没错,正好与我们之前的服务器编号相同,如果求余的结果为0, 我们就把当前图片名称对应的图片缓存在0号服务器上,如果余数为1,就把当前图片名对应的图片缓存在1号服务器上,如果余数为2,同理,那么,当我们访问任意一个图片的时候,只要再次对图片名称进行上述运算,即可得出对应的图片应该存放在哪一台缓存服务器上,我们只要在这一台服务器上查找图片即可,如果图片在对应的服务器上不存在,则证明对应的图片没有被缓存,也不用再去遍历其他缓存服务器了,通过这样的方法,即可将3万张图片随机的分布到3台缓存服务器上了,而且下次访问某张图片时,直接能够判断出该图片应该存在于哪台缓存服务器上,这样就能满足我们的需求了,我们暂时称上述算法为HASH算法或者取模算法,取模算法的过程可以用下图表示。

但是,使用上述HASH算法进行缓存时,会出现一些缺陷,试想一下,如果3台缓存服务器已经不能满足我们的缓存需求,那么我们应该怎么做呢?没错,很简单,多增加两台缓存服务器不就行了,假设,我们增加了一台缓存服务器,那么缓存服务器的数量就由3台变成了4台,此时,如果仍然使用上述方法对同一张图片进行缓存,那么这张图片所在的服务器编号必定与原来3台服务器时所在的服务器编号不同,因为除数由3变为了4,被除数不变的情况下,余数肯定不同,这种情况带来的结果就是当服务器数量变动时,所有缓存的位置都要发生改变,换句话说,当服务器数量发生改变时,所有缓存在一定时间内是失效的,当应用无法从缓存中获取数据时,则会向后端服务器请求数据,同理,假设3台缓存中突然有一台缓存服务器出现了故障,无法进行缓存,那么我们则需要将故障机器移除,但是如果移除了一台缓存服务器,那么缓存服务器数量从3台变为2台,如果想要访问一张图片,这张图片的缓存位置必定会发生改变,以前缓存的图片也会失去缓存的作用与意义,由于大量缓存在同一时间失效,造成了缓存的雪崩,此时前端缓存已经无法起到承担部分压力的作用,后端服务器将会承受巨大的压力,整个系统很有可能被压垮,所以,我们应该想办法不让这种情况发生,但是由于上述HASH算法本身的缘故,使用取模法进行缓存时,这种情况是无法避免的,为了解决这些问题,一致性哈希算法诞生了。
我们来回顾一下使用上述算法会出现的问题。
问题1:当缓存服务器数量发生变化时,会引起缓存的雪崩,可能会引起整体系统压力过大而崩溃(大量缓存同一时间失效)。
问题2:当缓存服务器数量发生变化时,几乎所有缓存的位置都会发生改变,怎样才能尽量减少受影响的缓存呢?
其实,上面两个问题是一个问题,那么,一致性哈希算法能够解决上述问题吗?
我们现在就来了解一下一致性哈希算法。
5.2 一致性哈希算法的基本概念
其实,一致性哈希算法也是使用取模的方法,只是,刚才描述的取模法是对服务器的数量进行取模,而一致性哈希算法是对2^32取模,什么意思呢?我们慢慢聊。
首先,我们把二的三十二次方想象成一个圆,就像钟表一样,钟表的圆可以理解成由60个点组成的圆,而此处我们把这个圆想象成由2^32个点组成的圆,示意图如下:

圆环的正上方的点代表0,0点右侧的第一个点代表1,以此类推,2、3、4、5、6……直到232-1,也就是说0点左侧的第一个点代表232-1
我们把这个由2的32次方个点组成的圆环称为hash环。
那么,一致性哈希算法与上图中的圆环有什么关系呢?我们继续聊,仍然以之前描述的场景为例,假设我们有3台缓存服务器,服务器A、服务器B、服务器C,那么,在生产环境中,这三台服务器肯定有自己的IP地址,我们使用它们各自的IP地址进行哈希计算,使用哈希后的结果对2^32取模,可以使用如下公式示意。
hash(服务器A的IP地址) % 232
通过上述公式算出的结果一定是一个0到2^32-1之间的一个整数,我们就用算出的这个整数,代表服务器A,既然这个整数肯定处于0到2^32-1之间,那么,上图中的hash环上必定有一个点与这个整数对应,而我们刚才已经说明,使用这个整数代表服务器A,那么,服务器A就可以映射到这个环上,用下图示意
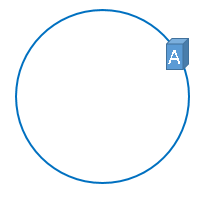
同理,服务器B与服务器C也可以通过相同的方法映射到上图中的hash环中
hash(服务器B的IP地址) % 232
hash(服务器C的IP地址) % 232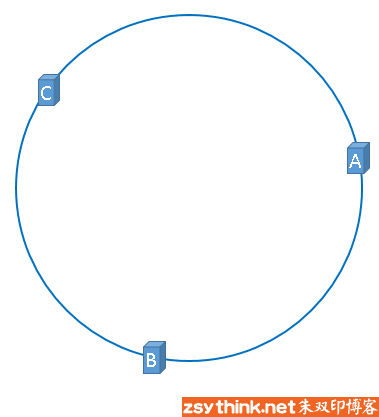
假设3台服务器映射到hash环上以后如上图所示(当然,这是理想的情况,我们慢慢聊)。
好了,到目前为止,我们已经把缓存服务器与hash环联系在了一起,我们通过上述方法,把缓存服务器映射到了hash环上,那么使用同样的方法,我们也可以将需要缓存的对象映射到hash环上。
映射后的示意图如下,下图中的橘黄色圆形表示图片
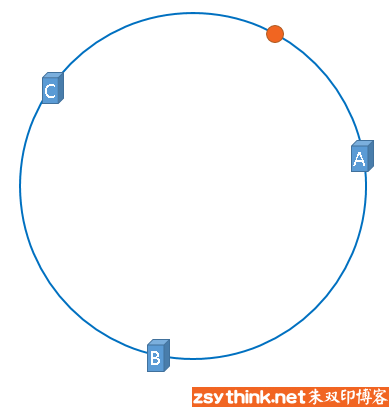
好了,现在服务器与图片都被映射到了hash环上,那么上图中的这个图片到底应该被缓存到哪一台服务器上呢?上图中的图片将会被缓存到服务器A上,为什么呢?因为从图片的位置开始,沿顺时针方向遇到的第一个服务器就是A服务器,所以,上图中的图片将会被缓存到服务器A上,如下图所示。

没错,一致性哈希算法就是通过这种方法,判断一个对象应该被缓存到哪台服务器上的,将缓存服务器与被缓存对象都映射到hash环上以后,从被缓存对象的位置出发,沿顺时针方向遇到的第一个服务器,就是当前对象将要缓存于的服务器,由于被缓存对象与服务器hash后的值是固定的,所以,在服务器不变的情况下,一张图片必定会被缓存到固定的服务器上,那么,当下次想要访问这张图片时,只要再次使用相同的算法进行计算,即可算出这个图片被缓存在哪个服务器上,直接去对应的服务器查找对应的图片即可。
刚才的示例只使用了一张图片进行演示,假设有四张图片需要缓存,示意图如下
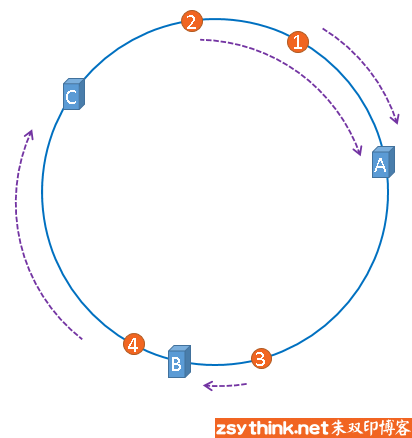
1号、2号图片将会被缓存到服务器A上,3号图片将会被缓存到服务器B上,4号图片将会被缓存到服务器C上。
5.3 一致性哈希算法的优点
经过上述描述,我想兄弟你应该已经明白了一致性哈希算法的原理了,但是话说回来,一致性哈希算法能够解决之前出现的问题吗,我们说过,如果简单的对服务器数量进行取模,那么当服务器数量发生变化时,会产生缓存的雪崩,从而很有可能导致系统崩溃,那么使用一致性哈希算法,能够避免这个问题吗?我们来模拟一遍,即可得到答案。
假设,服务器B出现了故障,我们现在需要将服务器B移除,那么,我们将上图中的服务器B从hash环上移除即可,移除服务器B以后示意图如下。
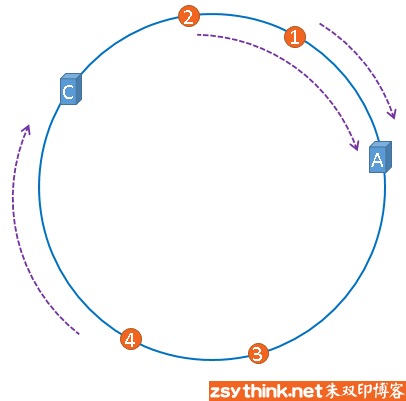
在服务器B未移除时,图片3应该被缓存到服务器B中,可是当服务器B移除以后,按照之前描述的一致性哈希算法的规则,图片3应该被缓存到服务器C中,因为从图片3的位置出发,沿顺时针方向遇到的第一个缓存服务器节点就是服务器C,也就是说,如果服务器B出现故障被移除时,图片3的缓存位置会发生改变

但是,图片4仍然会被缓存到服务器C中,图片1与图片2仍然会被缓存到服务器A中,这与服务器B移除之前并没有任何区别,这就是一致性哈希算法的优点,如果使用之前的hash算法,服务器数量发生改变时,所有服务器的所有缓存在同一时间失效了,而使用一致性哈希算法时,服务器的数量如果发生改变,并不是所有缓存都会失效,而是只有部分缓存会失效,前端的缓存仍然能分担整个系统的压力,而不至于所有压力都在同一时间集中到后端服务器上。
这就是一致性哈希算法所体现出的优点。
5.4 hash环的偏斜
在介绍一致性哈希的概念时,我们理想化的将3台服务器均匀的映射到了hash环上,如下图所示
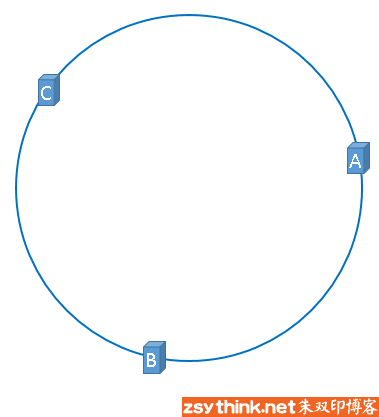
但是,理想很丰满,现实很骨感,我们想象的与实际情况往往不一样。
在实际的映射中,服务器可能会被映射成如下模样。
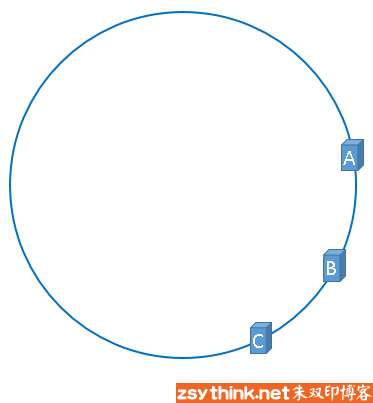
聪明如你一定想到了,如果服务器被映射成上图中的模样,那么被缓存的对象很有可能大部分集中缓存在某一台服务器上,如下图所示。
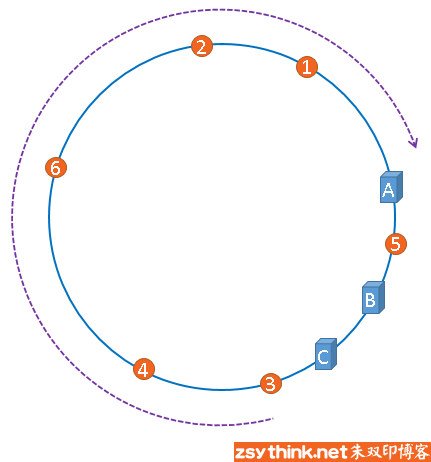
上图中,1号、2号、3号、4号、6号图片均被缓存在了服务器A上,只有5号图片被缓存在了服务器B上,服务器C上甚至没有缓存任何图片,如果出现上图中的情况,A、B、C三台服务器并没有被合理的平均的充分利用,缓存分布的极度不均匀,而且,如果此时服务器A出现故障,那么失效缓存的数量也将达到最大值,在极端情况下,仍然有可能引起系统的崩溃,上图中的情况则被称之为hash环的偏斜,那么,我们应该怎样防止hash环的偏斜呢?一致性hash算法中使用"虚拟节点"解决了这个问题,我们继续聊。
5.5 虚拟节点
话接上文,由于我们只有3台服务器,当我们把服务器映射到hash环上的时候,很有可能出现hash环偏斜的情况,当hash环偏斜以后,缓存往往会极度不均衡的分布在各服务器上,聪明如你一定已经想到了,如果想要均衡的将缓存分布到3台服务器上,最好能让这3台服务器尽量多的、均匀的出现在hash环上,但是,真实的服务器资源只有3台,我们怎样凭空的让它们多起来呢,没错,就是凭空的让服务器节点多起来,既然没有多余的真正的物理服务器节点,我们就只能将现有的物理节点通过虚拟的方法复制出来,这些由实际节点虚拟复制而来的节点被称为"虚拟节点"。加入虚拟节点以后的hash环如下。
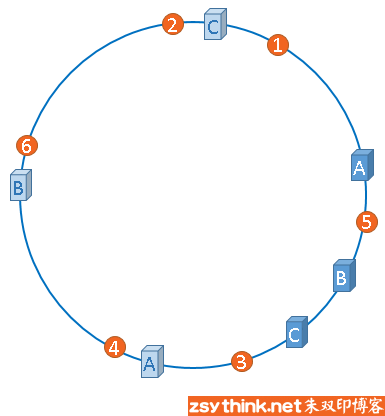
"虚拟节点"是"实际节点"(实际的物理服务器)在hash环上的复制品,一个实际节点可以对应多个虚拟节点。
从上图可以看出,A、B、C三台服务器分别虚拟出了一个虚拟节点,当然,如果你需要,也可以虚拟出更多的虚拟节点。引入虚拟节点的概念后,缓存的分布就均衡多了,上图中,1号、3号图片被缓存在服务器A中,5号、4号图片被缓存在服务器B中,6号、2号图片被缓存在服务器C中,如果你还不放心,可以虚拟出更多的虚拟节点,以便减小hash环偏斜所带来的影响,虚拟节点越多,hash环上的节点就越多,缓存被均匀分布的概率就越大。
参考:https://blog.csdn.net/u014209205/article/details/80820263
https://blog.csdn.net/qq_38180223/article/details/80911868
https://www.jianshu.com/p/8004c2d2ad59
https://china.googleblog.com/2007/07/bloom-filter_7469.html
http://www.cnblogs.com/zengdan-develpoer/p/4425167.html
https://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html