题目描述
给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
示例 1:
输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出: true
示例 2:
输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出: false
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/interleaving-string
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解析
交错字符串换言之就是,s1与s2在s3中的字符顺序还和原来的一样。比如

这样的话,我们可以将s1,s2从左至右挨个按照s3的顺序取出,若能够排列出一个完整的s3那么s3就是由s1与s2交错产生的。这就是关键思路。取出字母可以分别给s1,s2分配一个游标指针i,j。子串[0..i-1],[0..j-1]表示已经取出的串str。由于是按照s3的顺序取出的,这时str[0..i-1+j-1]与s3[0..i-1+j-1]是完全相同的。为方便实现,我们给s3也分配一个游标k。
对于状态(i,j)我们有三种选择
- 当s1[i] == s3[k],只能选择s1[i]这个字符。让i++,k++。
- 当s2[j] == s3[k],只能选择s2[j]这个字符。让j++,k++。
- 当s1[i] == s3[k]且s2[j] == s3[k],我们既可以选择取出s1[i],也可以选择取出s2[j]。这两种方式都要试一遍才能找出最终结果。
一直递归到i==s1.length, j == s2.length或者说k == s3.length,递归结束,这时已经可以判定s1与s2可以交错产生s3,层层返回即可。
对于这种情况,我优先选择使用记忆化搜索,一是方便编程,而是思路清晰,容易阅读。一般情况下,记忆化不必递推慢。如何使用记忆化,首先要明白重叠子结构在哪儿,所谓记忆化就是将这种重叠子结构的结果保存下来,下次如果用到,不必再重复计算,这就是记忆化的由来。关键问题是如何找到重叠子结构,比较有效的方法是,既然已经有上述分析的思路了,那不妨一步步的画一画,将递归树画出来,重叠子结构一眼明了。

上图中红色框框中就是重叠子结构。我们将这些结果保存下来,在下次用到的时候就不用重复计算了。本题一个特殊的地方是,程序实际运行中最右边的分支是不会遍历到的。因为在中间的分支已经可以确定是否是交错产生的了。
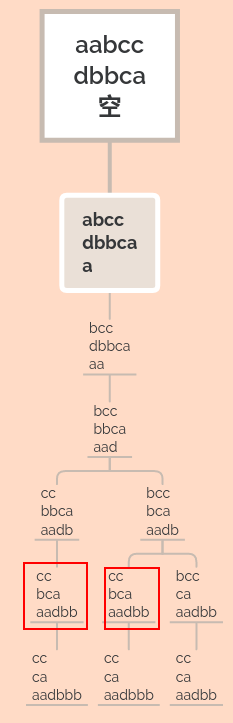
在上图中重叠子结构有两个,在计算第二个的时候,就可以重用第一次计算的结果。
程序说明:
dp[i][j]=true表示s1[0..i-1]与s2[0..j-1]不能交错组成s3[k],这里k=i-1+j-1。
代码
public class Solution {
private boolean[][] dp;
private char[] s1,s2,s3;
private boolean helper(int i, int j, int k) {
if (i == s1.length && j == s2.length) return true;
if (i > s1.length || j > s2.length || dp[i][j]) return false;
if (i < s1.length && s1[i] == s3[k] && helper(i + 1, j, k + 1)) {
return true;
}
if (j < s2.length && s2[j] == s3[k] && helper(i, j + 1, k + 1)) {
return true;
}
dp[i][j] = true;
return false; // s1[i] != s3[k] && s2[j] != s3[k]
}
// 1ms 100%(中文) 0ms 100%(英文)
public boolean isInterleave(String s1, String s2, String s3) {
if (s1.length()+s2.length() != s3.length()) return false;
dp = new boolean[s1.length()+1][s2.length()+1];
this.s1 = s1.toCharArray();
this.s2 = s2.toCharArray();
this.s3 = s3.toCharArray();
return helper(0,0,0);
}
}