Tri Tiling（hdu1143）

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2731    Accepted Submission(s): 1547

Problem Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes?

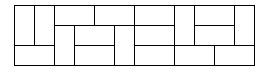
Here is a sample tiling of a 3x12 rectangle.

 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30. 

 

Output

For each test case, output one integer number giving the number of possible tilings. 

 

Sample Input

2
8
12
-1

 

Sample Output

3
153
2131

 

Source

University of Waterloo Local Contest 2005.09.24

 

 

 

思路：

1.标记和概念说明

f(n):当中的n即为题目中矩形的长，高固定位3，也即为题目中说的3xn中的n，f(n)表示当长为n时，全部的摆放方式的数量。切割线:一条竖直的线，这条线穿过题目中的矩形，将矩形一分为二，且这条线不能从砖的中间穿过，也 就是说仅仅有砖的边缘对齐的时候。才干穿过。

2.解题思想

2.1 对于每一种砖的摆放情况，可能有多条上面说的切割线，可是对于每一种情况，我们仅仅须要全部切割线中最右边的一条，我们记为L。也就是说在L的右边的部分就是不可切割的了。可是左边可能还是能够切割的。

对于L的左边我们继续使用函数f就可以。而右边是须要我们研究的主要部分，由于右边不能应用函数f。

2.2 不能应用函数f的原因是由于右边不在可切割。对于长度为2的不可切割矩形的摆放方式有三种方式，对长度大于2的不可切割矩形的摆放方式有两种方式。上一句话的理解或许须要你拿起笔在纸上画一画。

2.3 同一时候，考虑这种L可能在哪些位置？可能在从右边数起的长度为2的位置，也有可能在长度为4的位置，……， 也有可能在长度为n的位置。当然，也仅仅可能在上述的位置中。

因此有例如以下结果：       

 f(n)=f(n-2)*3+f(n-4)*2+...+f(2)*2+f(0)*2 ---- 表达式1   

然后，将上式用n-2替换得： f(n-2)=f(n-4)*3+f(n-6)*2+...+f(2)*2+f(0)*2 ---- 表达式2   

 表达式1减去表达式2得： f(n)=4*f(n-2)-f(n-4)2.4 在利用上面的递推公式时，我们须要两个递推的出口，即f(0) = 1, f(2) = 3.由上面的递推公式也知道 不涉及当n为奇数的情况，当n为奇数时，直接为零。由于当n为奇数时，矩形的面积为奇数，可是无论我们使 用了多少块砖。砖的总面积一定是个偶数，所以不存在不论什么的摆放形式。

转载请注明出处：寻找&星空の孩子 

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1143

这里有一点我认为比較坑。那就是F[0]=1;当n=0的时候为什么是1 ？？？

 

#include<stdio.h>
#define LL __int64
LL ans[35];
void init()
{
    ans[0]=1;
    ans[1]=ans[3]=0;
    ans[2]=3;ans[4]=11;
    for(int i=5;i<=30;i++)
    {
        if(i&1) ans[i]=0;
        else ans[i]=ans[i-2]*4-ans[i-4];
    }
}
int main()
{
    int n;
    init();
    while(scanf("%d",&n)!=EOF)
    {
        if(n==-1) break;
        printf("%I64d
",ans[n]);
    }
    return 0;
}