决策树思想的来源非常朴素,程序设计中的条件分支结构就是if-else结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法
决策树:是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果,本质是一颗由多个判断节点组成的树。

决策树分类原理
熵
物理学上,熵 Entropy 是“混乱”程度的量度。
系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
信息理论:
1、从信息的完整性上进行的描述:
当系统的有序状态一致时,**数据越集中的地方熵值越小,数据越分散的地方熵值越大。
2、从信息的有序性上进行的描述:
当数据量一致时,系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
1948年香农提出了信息熵(Entropy)的概念。
假如事件A的分类划分是(A1,A2,...,An),每部分发生的概率是(p1,p2,...,pn),那信息熵定义为公式如下:(log是以2为底,lg是以10为底)
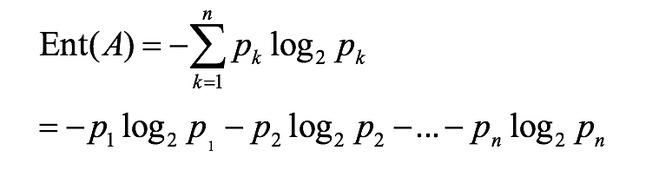
决策树的划分依据一------信息增益
信息增益:以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
信息增益 = entroy(前) - entroy(后)
- 定义与公式
特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差,即公式为:
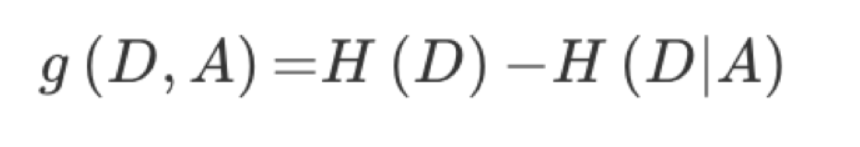
公式的详细解释:

注:信息增益表示得知特征X的信息而使得类Y的信息熵减少的程度
决策树的划分依据二----信息增益率
增益率:增益比率度量是用前面的增益度量Gain(S,A)和所分离信息度量SplitInformation(如上例的性别,活跃度等)的比值来共同定义的。
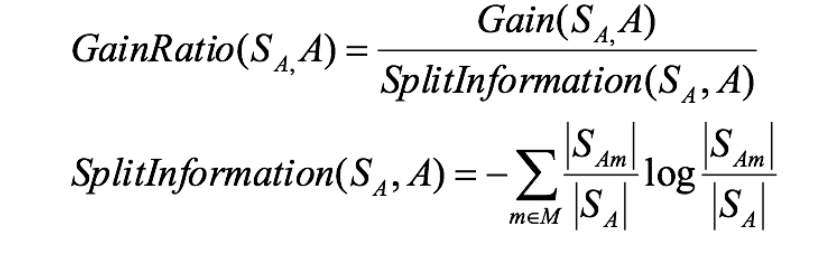
决策树的划分依据三——基尼值和基尼指数
基尼值Gini(D):从数据集D中随机抽取两个样本,其类别标记不一致的概率。故,Gini(D)值越小,数据集D的纯度越高。
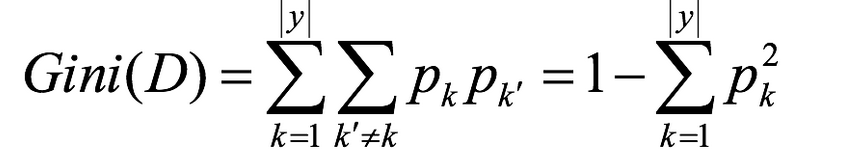
基尼指数Gini_index(D):一般,选择使划分后基尼系数最小的属性作为最优化分属性。
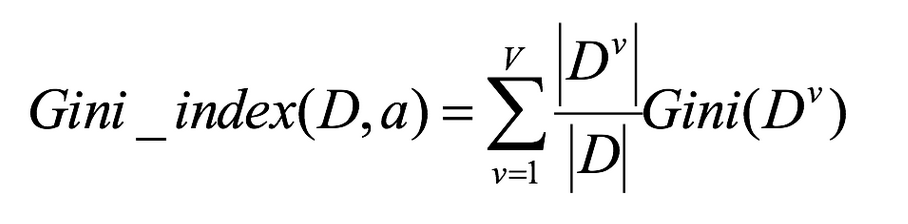
小结
一,决策树构建的基本步骤如下:
开始将所有记录看作一个节点
遍历每个变量的每一种分割方式,找到最好的分割点
分割成两个节点N1和N2
对N1和N2分别继续执行2-3步,直到每个节点足够“纯”为止。
二,决策树的变量可以有两种:
数字型(Numeric):变量类型是整数或浮点数,如前面例子中的“年收入”。用“>=”,“>”,“<”或“<=”作为分割条件(排序后,利用已有的分割情况,可以优化分割算法的时间复杂度)。
名称型(Nominal):类似编程语言中的枚举类型,变量只能从有限的选项中选取,比如前面例子中的“婚姻情况”,只能是“单身”,“已婚”或“离婚”,使用“=”来分割。
三,如何评估分割点的好坏?
如果一个分割点可以将当前的所有节点分为两类,使得每一类都很“纯”,也就是同一类的记录较多,那么就是一个好分割点。