（转）装箱问题

Description

有一个箱子容量为V（正整数，0<=V<=20000），同时有n个物品（0<=n<=30），每个物品有一个体积（正整数）。
要求n个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

Input

每个测试文件只包含一组测试数据，每组输入的第一行为一个整数V（0<=V<=20000），表示箱子的容量。
第二行输入一个整数n（0<=n<=30），表示有n个物品。
接下来n行，每行输入一个正整数，表示每个物品的体积。

Output

对于每组输入数据，输出一个整数，表示箱子剩余的最小空间。

Sample Input 1

24
6
8
3
12
7
9
7

Sample Output 1

0

Sample Input 2

90
12
3
7
4
5
13
2
8
4
7
6
5
7

Sample Output 2

19

解题思路：利用动态规划

我自己一开始的错误思想是用贪心算法，觉得先把最大的存进去，剩余的体积就是最小。题目提供的样例都过了，但是提交的时候却在某个样例错了。后来想了想才知道我这种想法有错误之处，先贴出我自己的错误代码

#include<iostream>
#include<algorithm>
using namespace std;

int V,n;
int a[40];
int sum = 0;
int main()
{
    cin>>V;
    cin>>n;
    for(int i = 0 ;i < n ;i++)
    {
        cin>>a[i];
        sum += a[i];
    }
    if(sum<=V) cout<<V-sum;
    else 
    if(sum>V)
    {
        sort(a,a+n);
        for(int i = n-1 ;i>=0;i--)
        {
            V -= a[i];
            if(V<0)
            {
                V += a[i];
                continue;
            }
        }
        cout<<V;
     } 
     return 0;
     
}

但是这种的话，后来想了一下，对于该数据正确答案是输出0，但是上述代码输出了1；因为代码先把99存进去了；

100
4
99 98 2 2

后来看了别人的博客，是利用动态规划

思路：

对于每一个物体，都有两种选择-放入或者不放入，所以外层循环可对每个物品进行遍历，而每选择一个物品，定会对大于该物品体积的dp数组元素产生影响，从而还需要一个内层数组对大于该物品体积的dp数组元素进行遍历更新。更新方法为：dp[i] = max{ dp[i] , dp[i - vi]+vi }，其中vi为当前物品的体积，max中的dp[i]表示不放入该物体时的解， dp[i - vi]+vi表示放入该物体时的解（i-vi表示给即将放入的物品留出合适的体积，如之前的例子，dp[i-vi]并不一定等于dp[i] - vi），取最大值，即为最优解。需要注意的是，需要先将dp数组中的每一个元素初始化为0。

对于如何运用 dp[i] = max{ dp[i] , dp[i - vi]+vi }，下面举个例子详细说明一下过程。
原文：https://blog.csdn.net/elma_tww/article/details/86507716

 

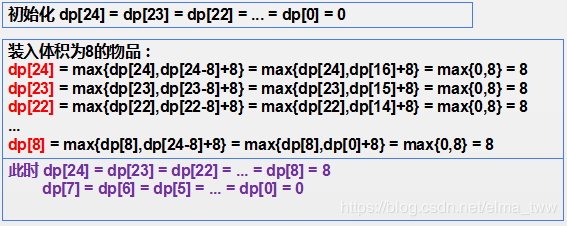
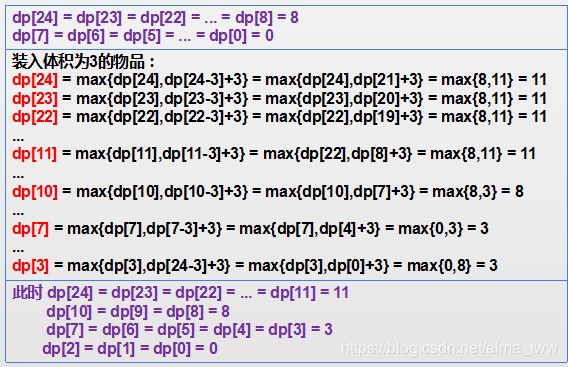
继续进行下去，直到遍历完所有物品。

主要是思想，代码其实挺简单的，代码如下：

#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;


int V,n;
int a[40];
int main()
{
    cin>>V;
    cin>>n;
    int dp[V+1];
    memset(dp,0,sizeof(dp)); 
    for(int i = 0 ;i < n;i++)
    {
        cin>>a[i];
        for(int j = V;j >= a[i];j--)
        {
            dp[j] = max(dp[j],dp[j-a[i]]+a[i]);
        }
    }
    cout<<V-dp[V];
    return 0;
}