leetcode 402.移掉K位数字/leetcode 5614. 找出最具竞争力的子序列(单调栈/dfs)

• 题目描述——leetcode 5614找出最具竞争力的子序列

给你一个整数数组 nums 和一个正整数 k ，返回长度为 k 且最具 竞争力 的 nums 子序列。

数组的子序列是从数组中删除一些元素（可能不删除元素）得到的序列。

在子序列 a 和子序列 b 第一个不相同的位置上，如果 a 中的数字小于 b 中对应的数字，那么我们称子序列 a 比子序列 b（相同长度下）更具 竞争力 。 例如，[1,3,4] 比 [1,3,5] 更具竞争力，在第一个不相同的位置，也就是最后一个位置上， 4 小于 5 。

 

示例 1：

输入：nums = [3,5,2,6], k = 2
输出：[2,6]
解释：在所有可能的子序列集合 {[3,5], [3,2], [3,6], [5,2], [5,6], [2,6]} 中，[2,6] 最具竞争力。
示例 2：

输入：nums = [2,4,3,3,5,4,9,6], k = 4
输出：[2,3,3,4]

• 解法一：超时的dfs

为什么一想到用dfs呢？因为最近正在练习dfs模板....觉得这道题和全排列是一个道理，只是每次排列需要在当前元素索引后面的位置搜索元素，然后再对结果进行排序，排序后第一个肯定是我们要找的数组（思路很垃圾，因为不会优化....）

那么这里套的就是dfs解决数字全排列的模板，菜鸡的我只会套模板....

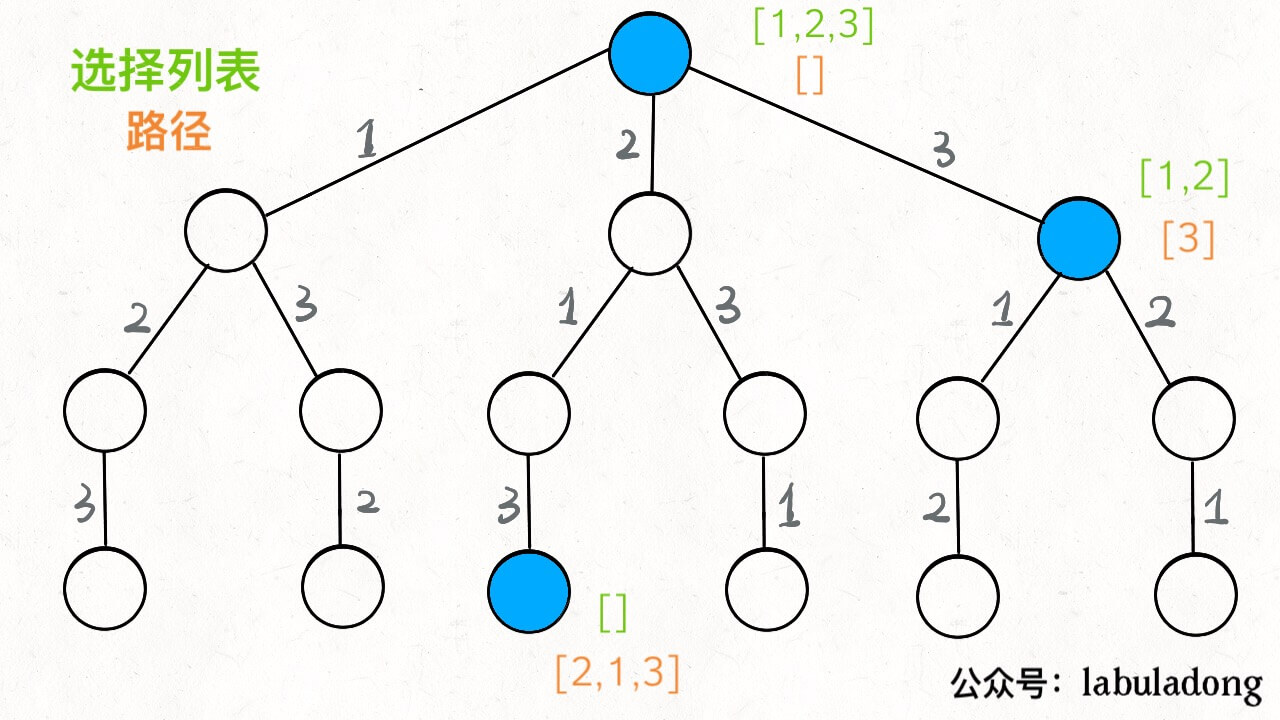
List<List<Integer>> res = new LinkedList<>();

/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
    // 记录「路径」
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track);
    return res;
}

// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素
// 结束条件：nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track) {
    // 触发结束条件
    if (track.size() == nums.length) {
        res.add(new LinkedList(track));
        return;
    }

    for (int i = 0; i < nums.length; i++) {
        // 排除不合法的选择
        if (track.contains(nums[i]))
            continue;
        // 做选择
        track.add(nums[i]);
        // 进入下一层决策树
        backtrack(nums, track);
        // 取消选择
        track.removeLast();
    }
}

遍历nums数组，每次搜索索引i+1后面的数组，然后找到所有的排列，这里vis可以用来判断当前元素是否被用掉。

class Solution:
    def mostCompetitive(self, nums: List[int], k: int) -> List[int]:
        self.res = list()
        vis = [0] * len(nums)
        r = list()

        def dfs(nums, u, r, vis):
            # r = list
            if u == k:
                self.res.append(copy.deepcopy(r))
                return

            for i in range(0, len(nums)):
                if vis[i] == 0:
                    r.append(nums[i])
                    vis[i] = 1
                    dfs(nums[i + 1:], u + 1, r, vis[i+1:])
                    vis[i] = 0
                    r.pop()

        dfs(nums, 0, r, vis)
        self.res.sort()
        return self.res[0]

超时了，看大佬的解答，这道题正确的打开方式其实是单调栈！不过还是期待哪位dfs大佬优化一个不超时的dfs版本。

• 解法二：单调栈

为什么想到用单调栈？

这里可能要说起leetcode 402题了，移除K位数字。

我们看看这道题题目：

给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小。

注意:

num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。
示例 1 :

输入: num = "1432219", k = 3
输出: "1219"
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
示例 2 :

输入: num = "10200", k = 1
输出: "200"
解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :

输入: num = "10", k = 2
输出: "0"
解释: 从原数字移除所有的数字，剩余为空就是0。

移除k个数字，和剩余k个数字，都是同样的道理。就相当于剩余length-k个数字或者是k个数字具有单调性质，那么我们是不是可以用一个单调栈始终维护一个单调的序列，每次被栈pop出去的就是被移除的，被栈push进去的就是需要留下的。

伪代码的实现是这样的：

<!-- 单调栈伪代码 -->
        for (遍历这个数组) {
            if (栈顶元素小于等于当前比较元素) {
                入栈;
            } else {
                while (栈不为空 && 栈顶元素大于当前元素&&还有能减去的元素) {
                    栈顶元素出栈;
                    更新结果;
                }
                当前数据入栈;
            }

            while(如果还要元素需要删除){
                栈顶元素出栈;
            }
        }

直接看leetcode 5614. 找出最具竞争力的子序列的代码

class Solution:
    def mostCompetitive(self, nums: List[int], k: int) -> List[int]:
        stack = list()
        count = len(nums) - k #需要被移除的数
        for i in range(0, len(nums)):
            if not stack or nums[i] >= stack[-1]:
                stack.append(nums[i]) 
            else:
                while stack and nums[i] < stack[-1] and count != 0:
                    stack.pop()
                    count -= 1
                stack.append(nums[i])
        while count != 0:
            stack.pop()
            count -= 1
        return stack

那么leetcode 402.移掉K位数字是不是就很简单了？

每次只要遍历的元素大于栈顶，就入栈，小于栈顶且需要删除元素，那么栈顶就出栈，将此元素入栈，这样pop掉的元素正好是删除的个数，如果删除的元素小于k，则继续将栈顶的元素pop出去。

后面为啥要判断res是不是为空，是为了通过‘100’这样的测试用例

class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
        num = [int(i) for i in num]
        stack = list()
        for i in range(0, len(num)):
            if not stack or stack[-1] < num[i]:
                stack.append(num[i])
            else:
                while stack and stack[-1] > num[i] and k != 0:
                    stack.pop()
                    k -= 1
                stack.append(num[i])
        while k != 0:
            stack.pop()
            k -= 1
        res = (''.join(str(i) for i in stack)).lstrip('0')
        if res:
            return res
        else:
            return '0'

参考链接：https://leetcode-cn.com/problems/find-the-most-competitive-subsequence/solution/js-mo-ni-yi-ge-dan-diao-di-zeng-zhan-by-akumu213/