- 题目描述
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
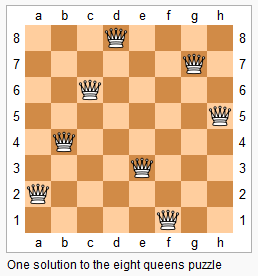
上图为 8 皇后问题的一种解法。 给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。 每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入:4
输出:[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
- 解法一:套回溯法模板
解决一个回溯问题,实际上就是一个决策树的遍历过程。
参考回溯法模板:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
伪代码回溯的框架:
result = [] def backtrack(路径, 选择列表): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择 backtrack(路径, 选择列表) 撤销选择
皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位,那么N皇后问题则可以看成,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
那么直接套用框架的话,就是这样:
vector<vector<string>> res; /* 输入棋盘边长 n,返回所有合法的放置 */ vector<vector<string>> solveNQueens(int n) { // '.' 表示空,'Q' 表示皇后,初始化空棋盘。 vector<string> board(n, string(n, '.')); backtrack(board, 0); return res; } // 路径:board 中小于 row 的那些行都已经成功放置了皇后 // 选择列表:第 row 行的所有列都是放置皇后的选择 // 结束条件:row 超过 board 的最后一行 void backtrack(vector<string>& board, int row) { // 触发结束条件 if (row == board.size()) { res.push_back(board); return; } int n = board[row].size(); for (int col = 0; col < n; col++) { // 排除不合法选择 if (!isValid(board, row, col)) continue; // 做选择 board[row][col] = 'Q'; // 进入下一行决策 backtrack(board, row + 1); // 撤销选择 board[row][col] = '.'; } }
其中对于皇后同一列,对角线,斜对角线的判断可以用isVlalid函数表示:
- 检查列是否有皇后冲突(很好判断,直接判断某列是否等于Q)
- 检查右上方是否有皇后冲突(则判断斜对角线是否有皇后,那么斜对角线怎么表示呢,则行索引从row-1递减,列索引从col+1递增)
- 检查左上方是否有皇后冲突(则判断对角线是否有皇后,与上同)
/* 是否可以在 board[row][col] 放置皇后? */ bool isValid(vector<string>& board, int row, int col) { int n = board.size(); // 检查列是否有皇后互相冲突 for (int i = 0; i < n; i++) { if (board[i][col] == 'Q') return false; } // 检查右上方是否有皇后互相冲突 for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) { if (board[i][j] == 'Q') return false; } // 检查左上方是否有皇后互相冲突 for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) { if (board[i][j] == 'Q') return false; } return true; }
那么这两段代码,用Python表示就是这样的(这里需要注意下Python的深拷贝和浅拷贝问题,回溯会修改board的值,需要用深拷贝之前的值):
import copy class Solution: def solveNQueens(self, n: int) -> List[List[str]]: self.N = n self.res = [] # board = ['.' for i in range(n)] board = [['.' for i in range(n)] for j in range(n)] self.backtrack(board, 0, self.res) return self.res def backtrack(self, board, row, res): if row == len(board): s = [] for item in board: st = '' for it in item: st += it s.append(st) res.append(copy.deepcopy(s)) return n = len(board[row]) for i in range(n): if not self.isValid(board, row, i): continue board[row][i] = 'Q' self.backtrack(board, row + 1, res) board[row][i] = '.' def isValid(self, board, row, col): num = len(board) #同一列是否冲突 for i in range(num): if board[i][col] =='Q': return False i, j = row - 1, col + 1 #右上方是否冲突 while i >= 0 and j < num: if board[i][j] == 'Q': return False i -= 1 j += 1 #左上方是否冲突 i, j = row - 1, col - 1 while i >= 0 and j >= 0: if board[i][j] == 'Q': return False i -= 1 j -= 1 return True
但是这样时间复杂度太高了:
- 解法二:dfs
其实dfs的递归条件,判断条件都可以想得到,而不好理解的地方是哪里呢?就是下面这三个存储N皇后行,对角线,斜对角线是否冲突的数组
col = [False] * n dg = [False] * 2 * n xdg = [False] * 2 * n
那么,这里为什么要这么设定需要结合官方题解去理解。对于N皇后是否会在对角线和斜对角线,其实满足以下两种性质:
- 对角线(第一个图):行下标-列下标=定值
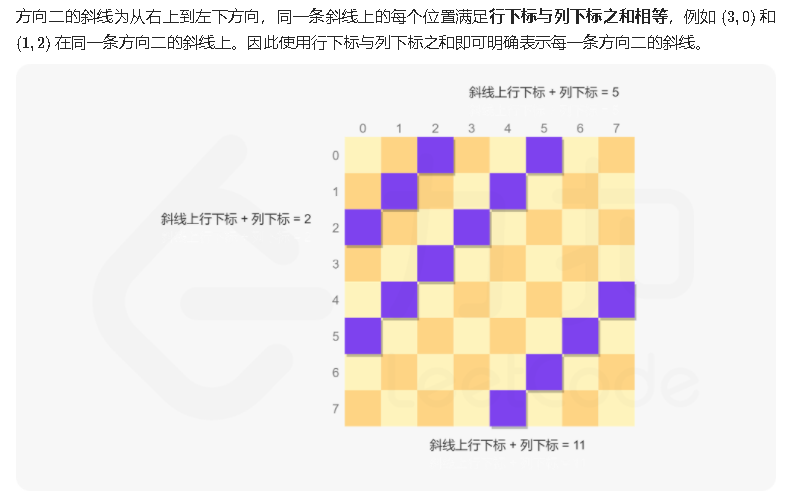
- 斜对角线(第二个图):行下标+列下标=定值
扩散到其他左上到右下和右上到左下的对角线都有类似性质,因此我们可以直接用一个一维数组去存储每个线是否有皇后的情况(True/False)。
那么为什么要用2n呢,是因为对角线的条数是小于2n的。

所以,代码是这样的:
import copy class Solution: def solveNQueens(self, n: int) -> List[List[str]]: grid = [['.' for i in range(n)] for j in range(n)] res = [] col = [False] * n dg = [False] * 2 * n xdg = [False] * 2 * n def dfs(u): r = list() if u == n: for i in range(n): r.append(''.join(copy.deepcopy(grid[i]))) res.append(r) return for i in range(n): if not col[i] and not dg[u+i] and not xdg[n-u+i]: grid[u][i] = 'Q' col[i] = dg[u+i] = xdg[n-u+i] = True dfs(u+1) grid[u][i] = '.' col[i] = dg[u+i] = xdg[n-u+i] = False dfs(0) return res
那么N皇后II就很简单了,直接需要返回N皇后的不同排序数量,改下返回值就OK。直接看代码:
class Solution: def totalNQueens(self, n: int) -> int: grid = [['.' for i in range(n)] for j in range(n)] self.res = 0 col = [False] * n dg = [False] * 2 * n xdg = [False] * 2 * n def dfs(u): if u == n: self.res += 1 return for i in range(n): if not col[i] and not dg[u+i] and not xdg[n-(u-i)]: grid[u][i] = 'Q' col[i] = dg[u+i] = xdg[n-u+i] = True dfs(u + 1) grid[u][i] = '.' col[i] = dg[u+i] = xdg[n-u+i] = False dfs(0) return self.res
参考链接:https://labuladong.gitbook.io/algo/di-ling-zhang-bi-du-xi-lie/hui-su-suan-fa-xiang-jie-xiu-ding-ban
https://leetcode-cn.com/problems/n-queens/solution/pythonji-chu-jie-fa-by-lockyguo-111/