堆之二项队列

前面提到左式堆和斜堆，支持合并、插入、删除最小值(最小堆)，且每次操作花费O(logn)。但是还有改进余地。

二项队列支持上面的三相操作，每次操作最坏的情形运行时间为O(logn)，而插入平均花费常数时间。

二项队列结构

二项队列不是一棵树，它是一个森林，由一组堆序的树组成的深林，叫做二项队列。二项堆是二项树的集合，所以先说明二项树。

二项树的递归定义如下：

• 二项树B₀只有一个结点；
• 二项树B_k由两棵二项树B_(k-1)组成的，其中一棵树是另一棵树根的左孩子。

二项树有以下性质：

1. B_k共有2^k个节点。
2. B_k的高度为k。
3. B_k在深度i处恰好有C_(k,i)个节点，其中i=0,1,2,...,k。
4. 根的度数为k，它大于任何其它节点的度数。

注意：树的高度和深度是相同的。若只有一个节点的树的高度是0。

二项堆是指满足以下性质的二项树的集合：

• 每棵二项树都满足最小堆性质。即，父节点的关键字 <= 它的孩子的关键字。
• 不能有两棵或以上的二项树具有相同的度数(包括度数为0)。换句话说，具有度数k的二项树有0个或1个。

实际上，它将包含n个节点的二项堆，表示成若干个2的指数和(或者转换成二进制)，则每一个2个指数都对应一棵二项树。例如，大小为13的优先队列就可以用B3，B2，B0来表示，二进制的表示为1101。

下图是大小为13（0001 0101）的二项队列

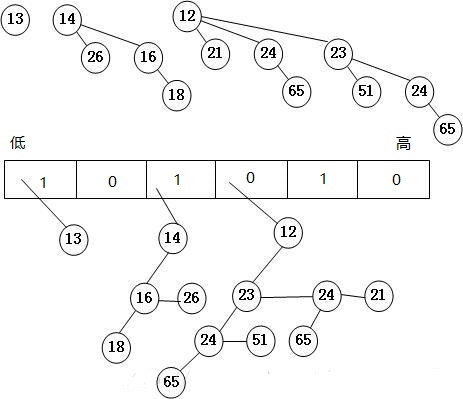
#define MaxTreeNum 32
typedef int Type;

typedef struct _BinomialNode{//二项树节点
    Type val;
    struct _BinomialNode *leftChild;//第一个孩子或者左孩子
    struct _BinomialNode *nextSibling;//右兄弟
}BinomialNode, *BinomialTree;

typedef struct _BinomialHeap{//二项队列
    int curSize;
    BinomialNode *trees[MaxTreeNum];//二项树数组
}BinomialHeap;

二项队列的操作

查找最小项：只需要查找每个二项树的根节点就可以了，因此时间复杂度为O(logN)。

合并：通过把两个队列相加在一起完成。因为有O(logN)棵树，所以合并的时间复杂度也是O(logN)。

插入：插入也是一种合并，只不过是把插入的结点当做B0。虽然感觉插入的时间复杂度是O(logN)，但是实际是O(1)，因为有一定的概率是被插入的二项队列没有B0。

删除最小：在根结点找到最小值，然后把最小值所在的树单独拿出分列为二项队列，然后把这个新的二项队列与原二项队列进行合并。每一个过程的时间复杂度为O(logN)。故加起来的时间复杂度仍为O(logN)。

其中最重要的就是合并。

合并的实现

BinomialNode* mergeBinomialTree(BinomialTree t1, BinomialTree t2){
    if (t1->val > t2->val)return mergeBinomialTree(t2, t1);
    t2->nextSibling = t1->leftChild;
    t1->leftChild = t2;
    return t1;
}

BinomialHeap *mergeBinomialHeap(BinomialHeap *bh1, BinomialHeap *bh2){
    BinomialTree T1, T2, Carry = NULL;
    int i, j;
    if (bh1->curSize + bh2->curSize > MaxTreeNum)
        cerr << "Exceed the Capacity" << endl;
    bh1->curSize = bh1->curSize + bh2->curSize;
    for (i = 0, j = 1; j < bh1->curSize; i++, j *= 2){
        T1 = bh1->trees[i];
        T2 = bh2->trees[i];
        //!!T1 = T1 == NULL ? 0 : 1
        switch (!!T1 + 2 * !!T2 + 4 * !!Carry){
        case 0: //No Trees  
        case 1: //Only bh1  
            break;
        case 2:
            bh1->trees[i] = T2;
            bh2->trees[i] = NULL;
            break;
        case 4: //Only Carry  
            bh1->trees[i] = Carry;
            Carry = NULL;
            break;
        case 3: //T1,T2  
            Carry = mergeBinomialTree(T1, T2);
            bh1->trees[i] = bh2->trees[i] = NULL;
            break;
        case 5:
            Carry = mergeBinomialTree(T1, Carry);
            bh1->trees[i] = NULL;
            break;
        case 6:
            Carry = mergeBinomialTree(T2, Carry);
            bh2->trees[i] = NULL;
            break;
        case 7:
            bh1->trees[i] = Carry;
            Carry = mergeBinomialTree(T1, T2);
            bh2->trees[i] = NULL;
            break;
        }
    }
    return bh1;
}

同样插入删除是合并的特殊情况；删除的操作比较复杂，后面再补充。

删除最小值的实现