一、简介
cost fuction是用来判断机器预算值和实际值得误差,一般来说训练机器学习的目的就是希望将这个cost function减到最小。本文会介绍如何找到这个最小值。
二、线性回归的cost function
假设现在有个一元一次方程式 h(x) = wx + b,要用来预测实际值y, 今天我输入了一组(x0, x1, x2......xm)and(y0, y1, y2, y3.......ym),那cost function = [(h(x0) - y0)**2 +......(h(xm) - ym)**2]/2m
函数的图如下,一元一次方的线性代数cost function图都是碗状的,不会有local minimun的问题。
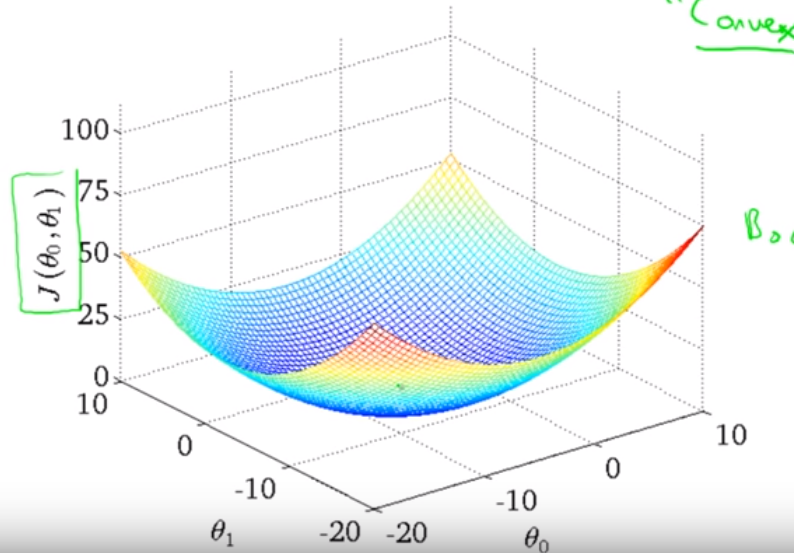
接着我们就要去改变w和b来找到让cost function J函数最低的值,方法为下
temp0 := w - α∂J(w,b)/∂w
temp1 := b - α∂J(w,b)/∂b
w := temp0
b := temp1
:=就是相当于程式语言里面的=,用右边的值取代左边。α是learning rate,在sklearn和tensorflow都可以配置,代表了学习速度,如下图所示,如果α越大代表优化的速度越快,但有可能会过头造成震荡,速度太慢会导致学习时间过长。正常情况下cost function J 都是一直下降的,如果J一直增加那就代表这边要注意的是α过大,要如何选α值呢?在教学里建议用0.01、0.1、1依序测试,看哪个的结果最好。另外要强调的是,必须要先对w,b两值进行完计算再替换,否则新的w会影响到b的计算。
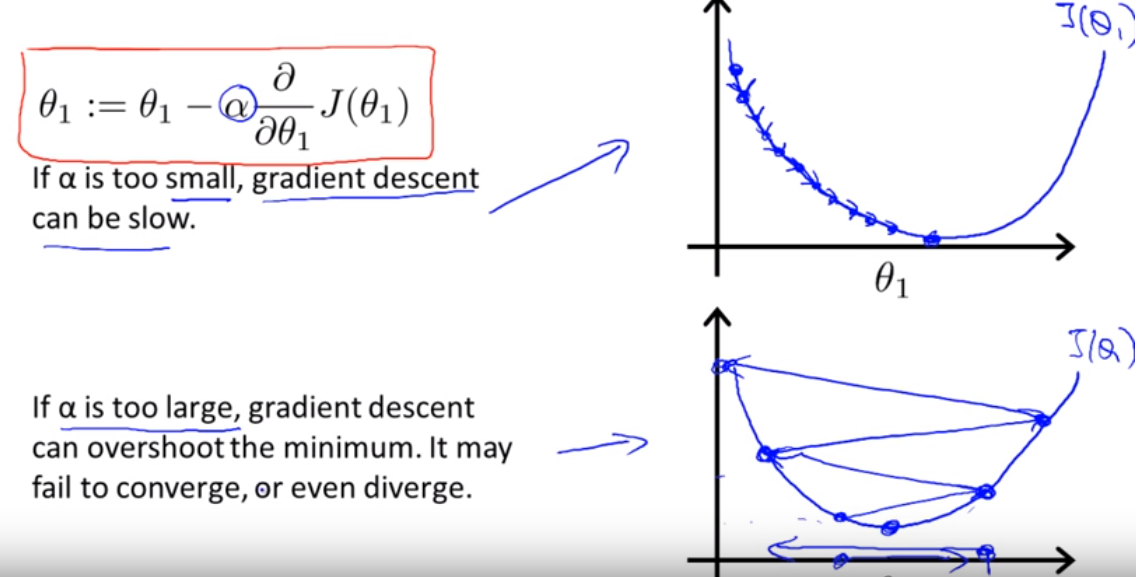
下图以一维图表示系数逼近的过程,当wi > wmin时,J会小于0,wi会不断减少,直到趋近于wmin,当wi < wmin时,J会大于0,wi会不断增加,造成的结果也是会使wi逼近wmin。在逼近的过程,J的斜率会越来越小,所以wi变化的幅度也会逐渐趋于缓和,直到最小值时J=0。

三、逻辑回归的cost function
逻辑回归的方程式和线性回归的很不一样,可是有趣的是,最后推导出的公式非常类似。首先先看逻辑回归的公式,当θTx越大,h(x)就越趋近于1,当θTx越小,h(x)就越趋近于0,当θTx = 0的时候h(x)就会等于0.5。

接下来是逻辑回归的cost function,可以看到对于y = 0 和 y = 1有两种不同的结果,所以我们要把他简化
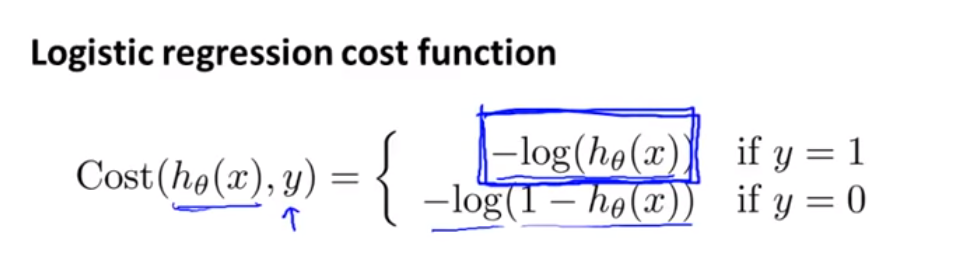
下面为逻辑回归cost function简化后的样子,可以看到当y = 0的时候前面的就会消失,当y = 1的时候后面的就会消失
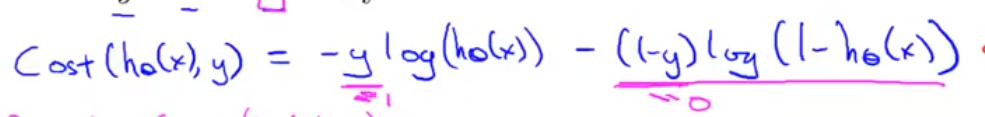
接着对cost function做微分就会发现跟线性回归的公式是一样的,只是h(x)的公式不同

最后要说的是,要顺利找到cost function的最小值,必须对输入的系数做缩放,假如今天影响房价的参数有面积(0-5000),房间数(1-5)。显然面积的量太大,对J值得影响力过大,所以需要对所有的数据做调整,理想的学习数据应该是在-1 ~ 1 之间,可以利用(数据 - 平均值) / 间距 来对所有的训练数据做统一量化。