Qual IPE中的Crop计算

Image Crop数据解算主要在FillFrameZoomWindow函数中完成。本文关注点为IFE输出到IPE进行的图像裁剪与缩放。

 IPE node接过IFE送来的图像数据时可以对图像数据进行进一步的裁剪缩放。主要涉及两个方面的cropInfo调整：

1. EIS对cropInfo调整
2. FOVC对cropInfo调整
3. ScaleRatio计算

1.EIS相关

EIS处理分为EIS和SW EIS两种。经前驱node IFE处理后，IPE根据EIS的设置进行裁剪调整。

1.1 SW EIS模式时

图1-1 SW EIS对裁剪的调整

    ImageInfo为请求的图像信息描述，SW EIS中ImageDimension会影响cropInfo。由于ImageDimension是相对于输出Image的size，所以需要将ImageDimension与ImageIndo的关系映射到cropInfo中，即得到右侧实现cropInfo。调整后的cropInfo和ImageDimension的关系如下：

    cropInfoW = （adjustedFullW - ImageDimensionW) x cropInfoW/adjustedFullW

                     = cropInfoW - ImageDimensionW x cropInfoW / adjustedFullW

                     = cropInfoW - ImageDimensionW x (cropInfoW / adjustedFullW)

    cropInfo.left = (adjustedFullW - ImageDimensionW) x (cropInfo.left / adjustedFullW)

                        = cropInfo.left - ImageDimension x (cropInfo.left / adjustedFullW)

     其中cropInfoW / adjustedFullW为调整的输入于输出比。类似的cropInfo.left / adjustedFullW有类似关系。

1.2 EIS对CropInfo的调整

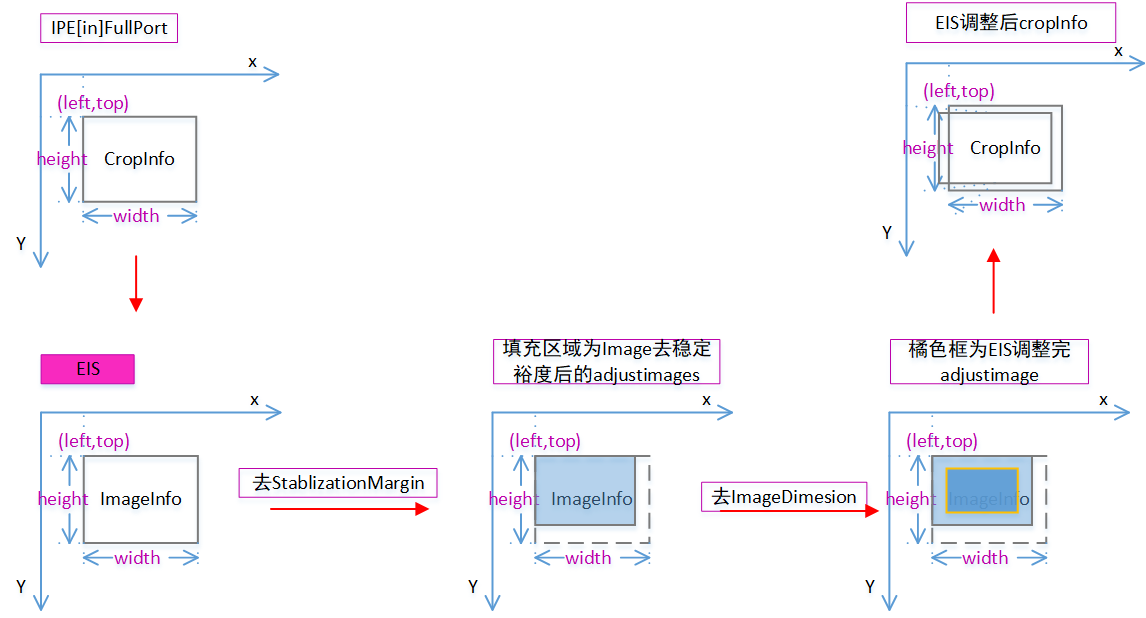
 图1-2 EIS对CropInfo的调整

    其中去StabLizationMargin阶段能会造成cropInfo数据不对齐，由于平台要求16字节对齐，所以这里没有表示对齐调整。EIS和SW EIS对cropInfo即裁剪区域进行调整时所涉及的ImageDimesion和StablizationMargin均是对输出图像的size，所以需要转换成对cropInfo。

代码实现如下：

2.FOVC

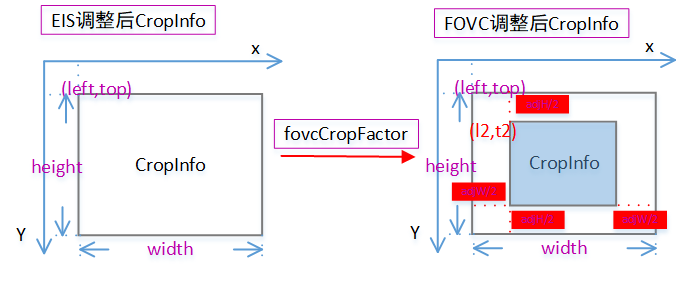
图2-1 FOVC对CropInfo的调整

    继EIS调整后，根据PropertyIDFOVCFrameInfo属性中fovcFactor对CropInfo进一步进行调整，得到图中浅蓝色区域。

3.Ratio计算

  ScaleRatio作为输入参数同Image一起设置给IPE，然后IPE根据设置完成Image的缩放&裁剪。

  这里ScaleRatio包含：preScaleRatio(预缩放比)， IFE时；postScaleRatio，IPE将要做的缩放比例。 

  计算ScaleRatio时会根据是否是超分辨率SR得到两组不同的ScaleRatio，

3.1非SR

    preScaleRatio从IFEOuput中获得（IFEScalerOutput->scalingFactor）。

    postScaleRatio为width或者height变倍比中较小的比值，即当w/h变倍比不同时按都满足计算，然后再裁剪成请求size。

3.2SR

   GeoLib也要参与计算。。。不知道GeoLib什么鬼，先跳过。

    preScaleRatio =