举两个不能使用洛必达法则的例子.
例1.$$\lim_{x\to 0}\frac{x}{1+x}$$
如果此例用了洛必达法则,则$$\lim_{x\to 0}\frac{x}{1+x}=\lim_{x\to 0}\frac{1}{1}=1.$$这显然是错误的.
$\frac{0}{0}$型洛必达法则:
当$x\to a$时,函数$f(x)$与$F(x)$都趋于零.在点$a$的某去心邻域内,$f^\prime(x)$及$F^\prime(x)$都存在,且$F^\prime(x)\ne 0$
$\lim_{x\to a}{\frac{f^\prime(x)}{F^\prime(x)}}$存在(或为无穷大),那么
$$\lim_{x\to a}{\frac{f(x)}{F(x)}}=\lim_{x\to a}{\frac{f^\prime(x)}{F^\prime(x)}}$$
显然,例1中$\lim_{x\to 0}1+x\neq 0$,故不能使用洛必达法则.
例2:$$\lim_{x\to 0}\frac{x^2\sin(x^{-4})}{x}$$
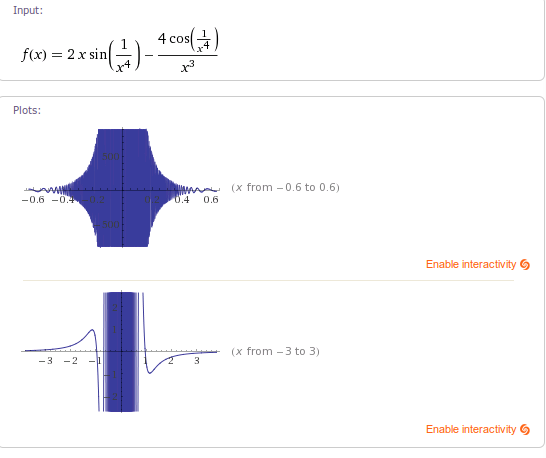
这道题也不能用洛必达法则做,因为$2x\sin(x^{-4})-4x^{-3}\cos(x^{-4})$在0的任意小的邻域内都有无限个零点,不满足$\frac{0}{0}$洛必达法则的使用条件.
当然,$\frac{\infty}{\infty}$型洛必达法则也有相应的注意事项,在此略去.