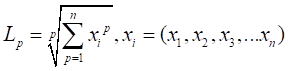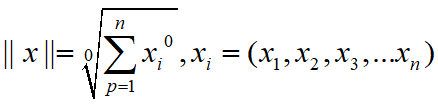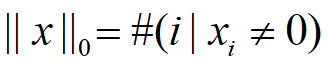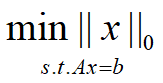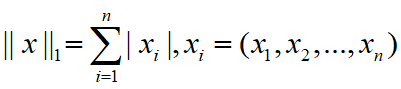过拟合与欠拟合
目录
一、 过拟合(overfitting)与欠拟合(underfitting) 2
❸限制权值Weight-decay,也叫正则化(regularization) 6
-
过拟合(overfitting)与欠拟合(underfitting)
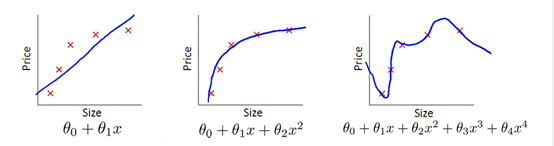
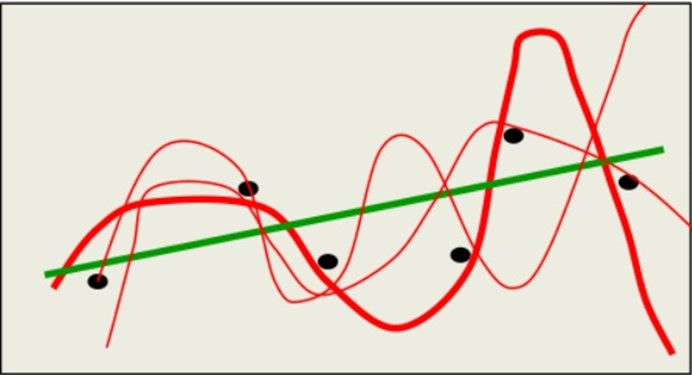
首先要确定的两个概念是Underfit(欠拟合)和Overfit(过拟合),也被称为high bias和high viarance。在表征线性回归模型的下面三张图中,左图使用一条直线来做预测模型,很明显无论如何调整起始点和斜率,该直线都不可能很好的拟合给定的五个训练样本,更不要说给出的新数据;右图使用了高阶的多项式,过于完美的拟合了训练样本,当给出新数据时,很可能会产生较大误差;而中间的模型则刚刚好,既较完美的拟合训练数据,又不过于复杂,基本上描绘清晰了在预测房屋价格时Size和Prize的关系。
对于逻辑回归,同样存在此问题,如下图:

机器学习中的泛化:
在机器学习中,我们描述从训练数据学习目标函数的学习过程成为归纳性的学习。
泛化是指,机器学习模型学到的概念在遇到新的数据时表现的好坏(预测准确度等)。
拟合:拟合是指你逼近目标函数的远近程度。
-
过拟合
模型过度拟合,在训练集(training set)上表现好,但是在测试集上效果差,也就是说在已知的数据集合中非常好,但是在添加一些新的数据进来训练效果就会差很多,造成这样的原因是考虑影响因素太多,超出自变量的维度过于多了。
-
欠拟合(高偏差)
模型拟合不够,在训练集(training set)上表现效果差,没有充分的利用数据,预测的准确度低。
-
偏差(Bias)
首先error=bias+variance
Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精确度。
-
方差(Variance)
Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
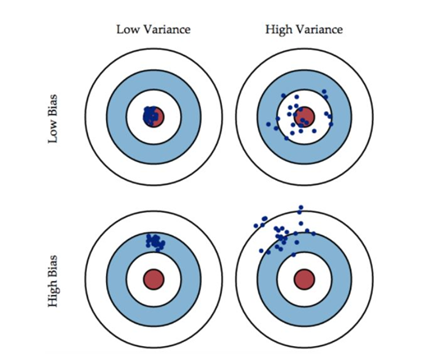
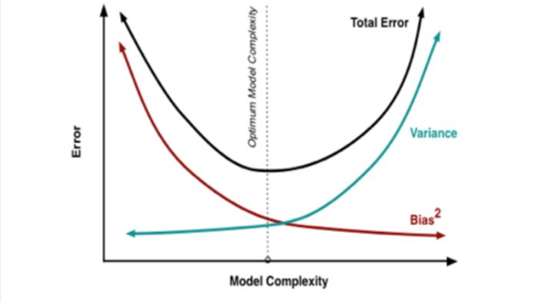
如上图所示:偏差值的是模型的输出值与红色中心的距离;而方差指的是模型的每一个输出结果与期望之间的距离。
就像我们射箭,低偏差指的是我们瞄准的点与红色中心的距离很近,而高偏差指的是我们瞄准的点与红色中心的距离很远。低方差是指当我们瞄准一个点后,射出的箭中靶子的位置与我们瞄准的点的位置距离比较近;高方差是指当我们瞄准一个点后,射出的箭中靶子的位置与我们瞄准的点的位置距离比较远。
❶低偏差低方差时,是我们所追求的效果,此时预测值正中靶心(最接近真实值),且比较集中(方差小)。
❷低偏差高方差时,预测值基本落在真实值周围,但很分散,此时方差较大,说明模型的稳定性不够好。
❸高偏差低方差时,预测值与真实值有较大距离,但此时值很集中,方差小;模型的稳定性较好,但预测准确率不高,处于"一如既往地预测不准"的状态。
❹高偏差高方差时,是我们最不想看到的结果,此时模型不仅预测不准确,而且还不稳定,每次预测的值都差别比较大。
过拟合表现为:在训练集上表现很好,但是在测试集上效果很差。
欠拟合表现为:在训练集上表现就不太好。
-
防止过拟合和欠拟合的方法
-
如何防止过拟合
综述:一般来说防止过拟合的方法有:
❶获取更多数据❷减少特征变量❸限制权值(正则化)❹贝叶斯方法❺结合多种模型
以深度学习中的神经网络为例,防止过拟合的方法如下:
❶获取更多数据
这是解决过拟合最有效的方法,只要给足够多的数据,让模型[训练到]尽可能多的[例外情况],它就会不断修正自己,从而得到更好的结果。
如何获取更多的数据,可以有以下几个方法:
①从数据源头获取更多数据:这个是最容易想到的,例如物体分类,我就再多拍几张照片就好了;但是在很多情况下,大幅增加数据本身就不容易;另外,我们不清楚获取多少数据才算够用能使模型表现较好。
②根据当前数据集估计数据分布参数,使用该分布产生更多数据:这个一般不用,因为估计分布参数的过程也会带入抽样误差。
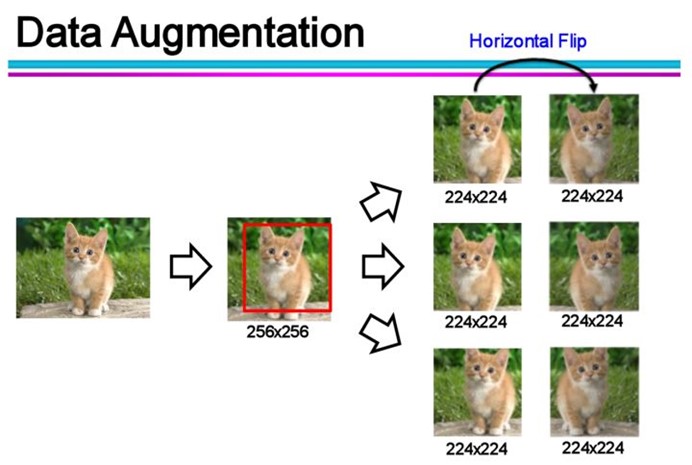
③数据增强(Data Augmentation):通过一定规则扩充数据。如在物体分类问题里,物体在图像中的位置、姿态、尺度,整体图片明暗度等都不会影响分类结果。我们就可以通过图像平移、翻转、缩放、切割等手段将数据库成倍扩充。
❷使用合适的模型(减少特征变量)
前面说了,过拟合主要使有两个原因造成的:数据太少+模型太复杂。所以我们可以通过使用合适复杂度的模型来防止过拟合问题,让其足够拟合真正的规则,同时又不至于拟合太多抽样误差。
①减少网络的层数、神经元的个数等均可以限制网络的拟合能力;
②Early stopping早停止
对于每个神经元而言,其激活函数在不同区间的性能使不同的:
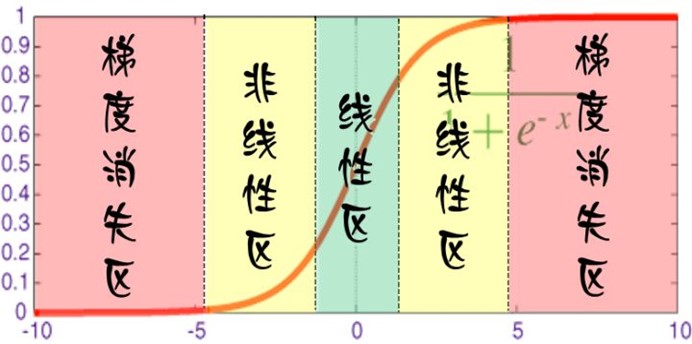
当网络权值较小时,神经元的激活函数工作在线性区,此时神经元的拟合能力较弱(类似线性神经网络)。
有了上述共识之后,我们就剋解释为什么限制训练时间(early stopping)有用:因为我们在初始化网络的时候一般都是初始化为较小的权值。训练时间越长,部分网络权值可能越大,如果我们在合适的时间停止训练,就可以将网络的能力限制在一定范围内。
❸限制权值Weight-decay,也叫正则化(regularization)
下面第三部分会详细介绍L0,L1,L2正则化即L0,L1,L2范数。
❹贝叶斯方法
下面第四部分详细介绍如何利用贝叶斯方法防止过拟合。
❺结合多种模型
简而言之,训练多个模型,以每个模型的平均输出作为结果。
①Bagging
简单理解,就是分段函数的概念:用不同的模型拟合不同部分的训练集。以随机森林(Rand Forests)为例,就是训练了一堆不关联的决策树。但由于训练神经网络本身需要耗费较多自由,所以一般不单独使用神经网络做Bagging。
②Boosting
既然训练复杂神经网络比较慢,那我们就可以只使用简单的神经网络(层数、神经元数限制等),通过训练一系列简单的神经网络,加权平均其输出。
③Dropout
这是一个很高效的方法
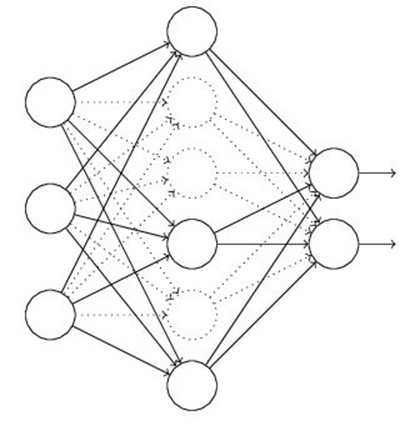
在训练时,每次随机(如50%概率)忽略隐藏层的某些节点;这样我们相当于随机从2^H个模型中采样选择模型.
-
如何防止欠拟合
❶引入新的特征❷添加多项式特征❸减少正则化参数❹
-
L0,L1,L2正则化,也叫L0,L1,L2范数
在机器学习的概念中,我们经常听到L0,L1,L2正则化,下面我们对这几种正则化做简单介绍
数学基础:
❶范数,用||x||表示范数
向量范数是衡量某个向量空间中向量的大小或长度;矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是,对应向量范数,向量空间中向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小,就好比米和厘米都可以来度量长度一样;对于矩阵范数,学过线性代数,我们知道,通过运算AX=B,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
这里简单的介绍以下几种向量范数的定义和含义。
①L-P范数
L-P范数不是一个范数,而是一组范数,其定义如下:
|
|
|
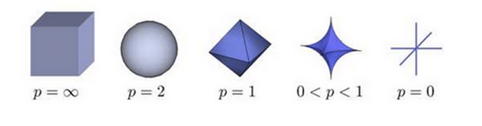
根据P的变化,范数也有着不同的变化,一个经典的有关P范数的变化图如下:
上图表示了p从无穷到0变化时,三维空间中到原点的距离(范数)为1的点构成的图形的变化情况。以常见的L-2范数(p=2)为例,此时的范数也即欧氏距离,空间中到原点的欧氏距离为1的点构成了一个球面。 |
②L0范数
当p=0时,也就是L0范数,由上面可知,L0范数并不是一个真正的范数,它主要是被用来度量向量中非零元素的个数。用上面L-P定义可以得到的L0的定义为:
|
这里就有点问题了,我们知道非零元素的零次方为1,但零的零次方,非零数开零次方都是什么鬼,很不好说明L0的意义,所以在通常情况下,大家都用的是:
表示向量x中非零元素的个数。 对于L0范数,其优化问题为:
即能令Ax=b成立的维度最少数量的x,即寻找一个向量,能够使Ax=b,并且x中所包含的特征比较少。在实际应用中,由于L0范数本身不容易有一个好的数学表示形式,给出上面问题的形式化表示是一个很难的问题,故被人认为是一个NP难问题。所以在实际情况中,L0的最优问题会被放宽到L1或L2下的最优化。 |
③L1范数
L1范数是我们经常见到的一种范数,它的定义如下:
|
|
表示向量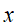 中非零元素的绝对值之和。(一个向量中非零元素的绝对值之和,例如向量[1,-1,2],它的L1范数是|1||+||-1||+||2||=4||。
中非零元素的绝对值之和。(一个向量中非零元素的绝对值之和,例如向量[1,-1,2],它的L1范数是|1||+||-1||+||2||=4||。
L1范数有很多的名字,例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference):
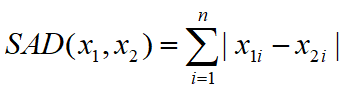
对于L1范数,它的优化问题如下:
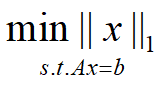
由于L1范数的天然性质,对L1优化的解是一个稀疏解,因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏,去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。
④L2范数
L2范数是我们最常用的范数了,我们用的最多的度量距离欧氏距离就是一种L2范数,它的定义如下:
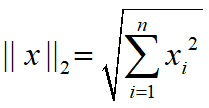
表示向量元素的平方和再开方。
像L1范数一样,L2范数也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference):
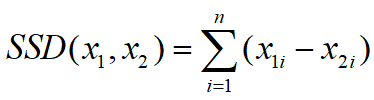
对于L2范数,它的优化问题如下:
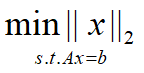
L2范数通常会被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
⑤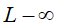 范数
范数
当P= 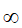 时,也就是
时,也就是 范数,它主要被用来度量向量元素的最大值。用上面的
范数,它主要被用来度量向量元素的最大值。用上面的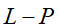 定义可以得到
定义可以得到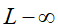 的定义为:
的定义为:

与L0一样,在通常情况下,大家都用的是:
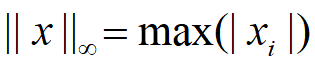
来表示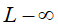 。
。
-
正则化
L0正则化的值是模型参数中非零参数的个数。
L1正则化表示各个参数绝对值之和。
L2正则化标识各个参数的平方的和的开方值。
先讨论几个问题:
-
实现参数的稀疏有什么好处吗?
一个好处是可以简化模型,避免过拟合。因为一个模型中真正重要的参数可能并不多,如果考虑所有的参数起作用,那么可以对训练数据可以预测的很好,但是对测试数据效果可能很差。另一个好处是参数变少可以使整个模型获得更好的可解释性。
-
参数越小值代表模型越简单吗?
是的。为什么参数越小,说明模型越简单呢?这是因为越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点,这就容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大。
-
L0正则化
根据上面的讨论,稀疏的参数可以防止过拟合,因此用L0范数(非零参数的个数)来做正则化项是可以防止过拟合的。从直观上看,利用非零参数的个数,可以很好的来选择特征,实现特征稀疏的效果,具体操作时选择参数非零的特征即可。但因为L0正则化很难求解,是个NP难问题,因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似,比L0容易求解,并且也可以实现稀疏的效果。
-
L1正则化
-
L2正则化
-
-
如何利用贝叶斯方法防止过拟合
-