p为质数 a为正整数,那么p^a的因子和就是:

p^a的因子数就是a+1;
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
那么对于一个正整数n有素因子分解:
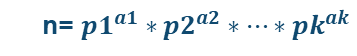
因子和就是:
 ①
①
n的因子数有:
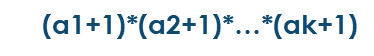
例题:tzoj 5845 求A^B的因子和
把A分解 即把A看成上面的n 因子和就是上面①处
还有个B次方 so B乘到a1那里 即: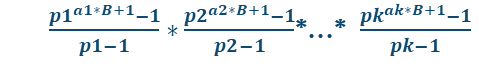
注意要求逆元 因为除数会过大 会损精度(质数逆元就是质数-2,除一个数就是乘这个数的逆元)
代码:

#include<bits/stdc++.h> using namespace std; #define mod 9901 #define ll long long ll poww(ll a, ll b) { ll ans = 1, base = a; while (b) { if (b & 1 != 0) ans = base*ans%mod; base = base*base%mod; b >>= 1; } return ans%mod; } ll a,b; ll f(ll n) { ll t=sqrt(n+0.5),ans=1; int i; ll a,tmp; for(i=2;i<=t;i++) { if(n%i==0) { a=0; while(n%i==0)n/=i,a++; tmp=poww(i,a*b+1); ans=(ans*(tmp-1)%mod)*poww((i-1),mod-2)%mod; } } if(n>1) { tmp=poww(n,b+1); ans=(ans*(tmp-1)%mod)*poww((n-1),mod-2)%mod; } return ans%mod; } int main() { cin>>a>>b; ll y=f(a); cout<<y<<endl; return 0; }
