• 平衡二叉树（AVL）

    1. 背景

    由于二叉排序树存在因插入顺序不合理导致“失衡”而退化成链表问题，于是有科学家提出了通过树高去调整二叉排序树出现“失衡”的情况（其实不止插入会导致“失衡”，删除也会导致“失衡”）。
    ps：这里的失衡是指二叉排序树的左右子树高度差的绝对值大于1

    2. 重点

    1.平衡二叉树，本质上也是二叉排序树，所以拥有二叉排序树的所有性质。
    2.平衡二叉树的学习重点，在于平衡条件以及平衡调整
    总之，我们可以这样理解，在二叉排序树的基础上，再给二叉排序树定义一种性质（左右子树高度差的绝对值不大于1），然后我们在二叉排序树的插入或者删除的时候都去维护这个性质，这样二叉排序树就“平衡”，这时候，它就变成了平衡二叉树。
    ps：数据结构，就是定义一种或多种性质，并去维护这些性质

    3. 思考

    高度同为H的二叉排序树和平衡二叉树，他们的节点数量分别在什么范围之内？
    二叉排序树：
    当退化成链表时，若二叉排序树的树高为H，则节点数量就为H；若二叉排序树是一棵满二叉树时，则节点数量为2H-1，所以我们得到高度为H的二叉排序树的节点数量范围为：H ⩽ SIZE(H) ⩽ 2H-1
    平衡二叉树：
    对于平衡二叉树，我们分析最少节点时，定义low(H)代表高度为H的平衡二叉树的最少节点数量，则根据左右子树高度差的绝对值小于等于1，则我们可以得到：low(H) = low(H-1) + low(H-2) + 1，这个等式的增长率大约为1.618H；最多节点时，一样是满二叉树的情况，最多节点数为：2H-1，所以高度为H的平衡二叉树的节点数量为：1.618H ⩽ SIZE(H) ⩽ 2H-1

    4. 性质

    1.平衡二叉树是二叉排序树
    2.平衡二叉树的左右子树之间的高度差不超过1

    5. 平衡调整策略

    1.平衡调整发生在回溯阶段的第一个失衡节点处
    2.理解平衡策略的关键在于：分析清楚四种情况下，ABCD四棵子树的树高关系
    1).LL型，大右旋
    2).LR型，先小左旋，再大右旋
    3).RL型，先小右旋，再大左旋
    4).RR型，大左旋
    这里只是先提出调整策略，下面才开始解释。

    5.1. 调整策略解释

    在解释调整策略之前，我们必须明白，对于一个根节点，其高度若为H，其左子树高度若为HL，右子树高度为HR，则H = max(HL, HR) + 1。
    为何平衡调整发生在回溯阶段的第一个失衡节点处？
    由于我们是递归实现插入和删除，对于平衡二叉树，我们需要维护树高属性，对于插入和删除可能会影响到树高，所以每次插入和删除都需要去判断是否需要更新树高，当树高发生改变时，从插入和删除的节点开始，其祖先节点的树高都发生了改变，所以我们在回溯过程中需要更新树高，若某个祖先节点中，出现了左右子树高度差大于1的情况，就需要调整。
    我们可以通过逻辑结构图来说明：
    我们有以下平衡二叉树，照着这个二叉树，我们来分别分析插入和删除导致调整的情况：
    图1
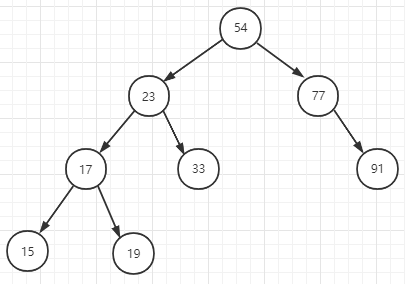
    image
    插入
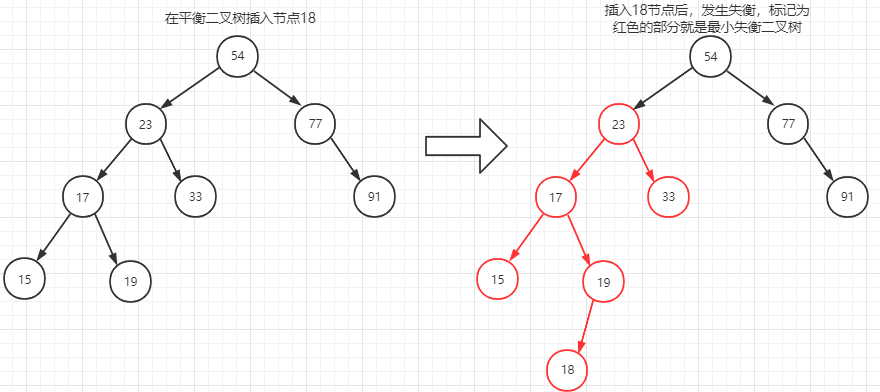
    在图1的二叉树基础上，我们插入一个节点18.
    image
    这时，由于新插入18，对于路径54->23->17->19->18，从插入18成功后，有一个回溯过程，回溯方向为18->19->17->23->54，在这个回溯过程中，我们都得更新这些节点的树高，并且更新到23时，发现对于23节点，其左子树的树高HL为3，右子树树高HR为1，|HL-HR|=2，这时候发现不平衡，所以得调整。
    删除
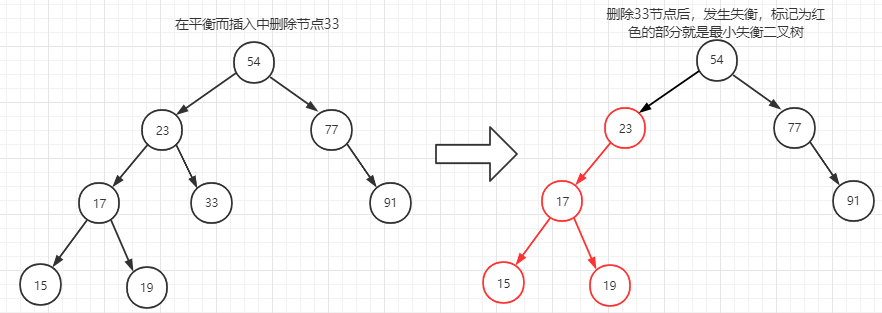
    还是从图1的二叉树基础上，我们删除91节点。
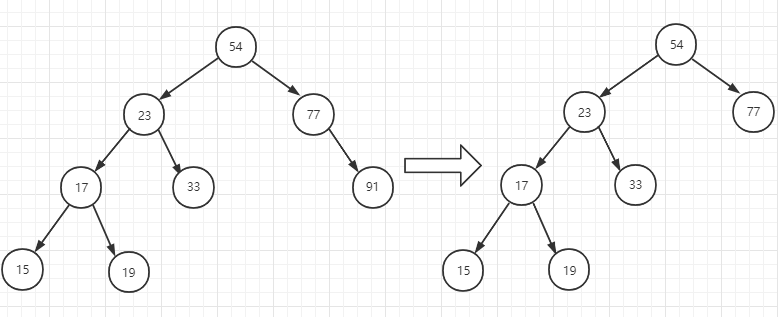
    image
    删除完节点91后，回溯过程为77->54，这时候77节点的树高被更新为1，而更新到54节点时，发现54左子树HL高度为3，而右子树高度HR为1，则时候左右子树高度差|HL-HR|=2，需要调整。
    注意：这里，我们要特别清楚和记住，由于插入和删除都是递归操作，所以插入和删除有可能会影响其祖先节点的树高，我们都得先更新树高，再去判断更新树高后的节点的左右子树是否发生失衡（其左右子树高度差大于1）
    这里，模拟一下平衡二叉树的插入时向下递归和向上回溯。
    插入时向下递归
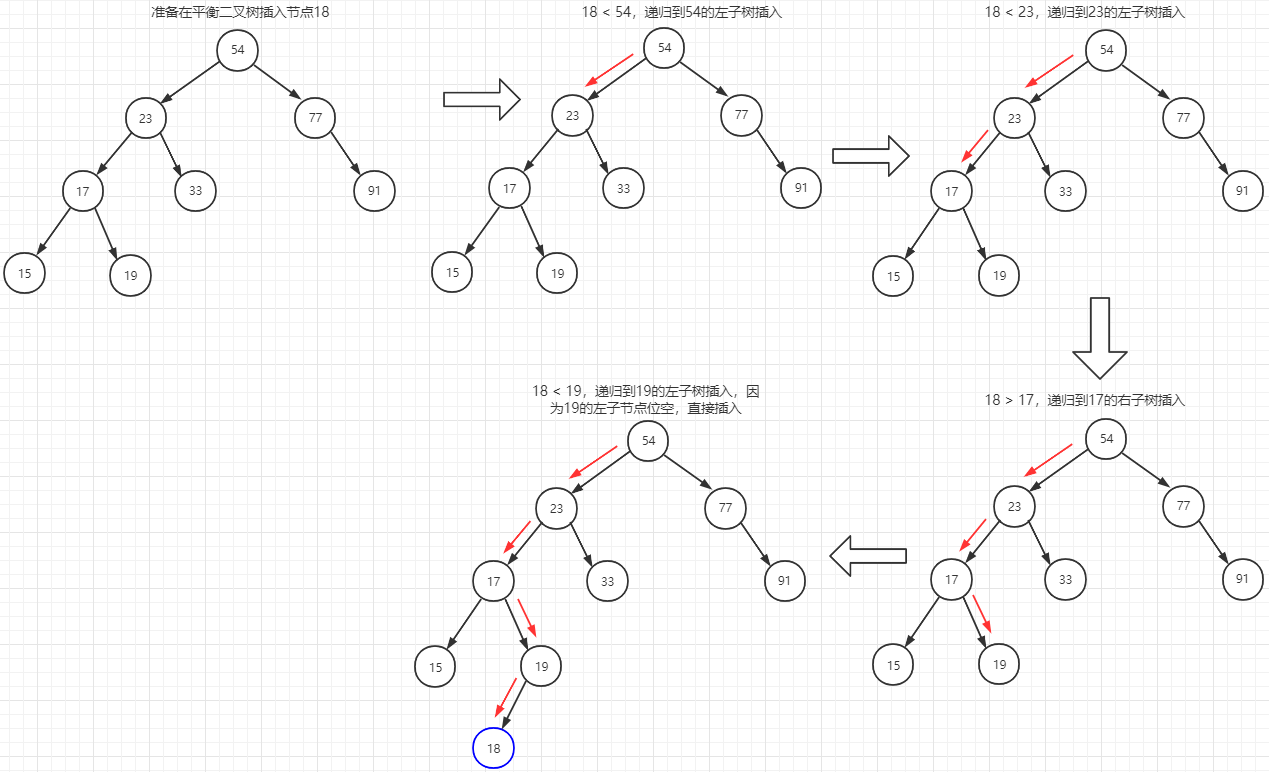
    image
    插入时向上回溯
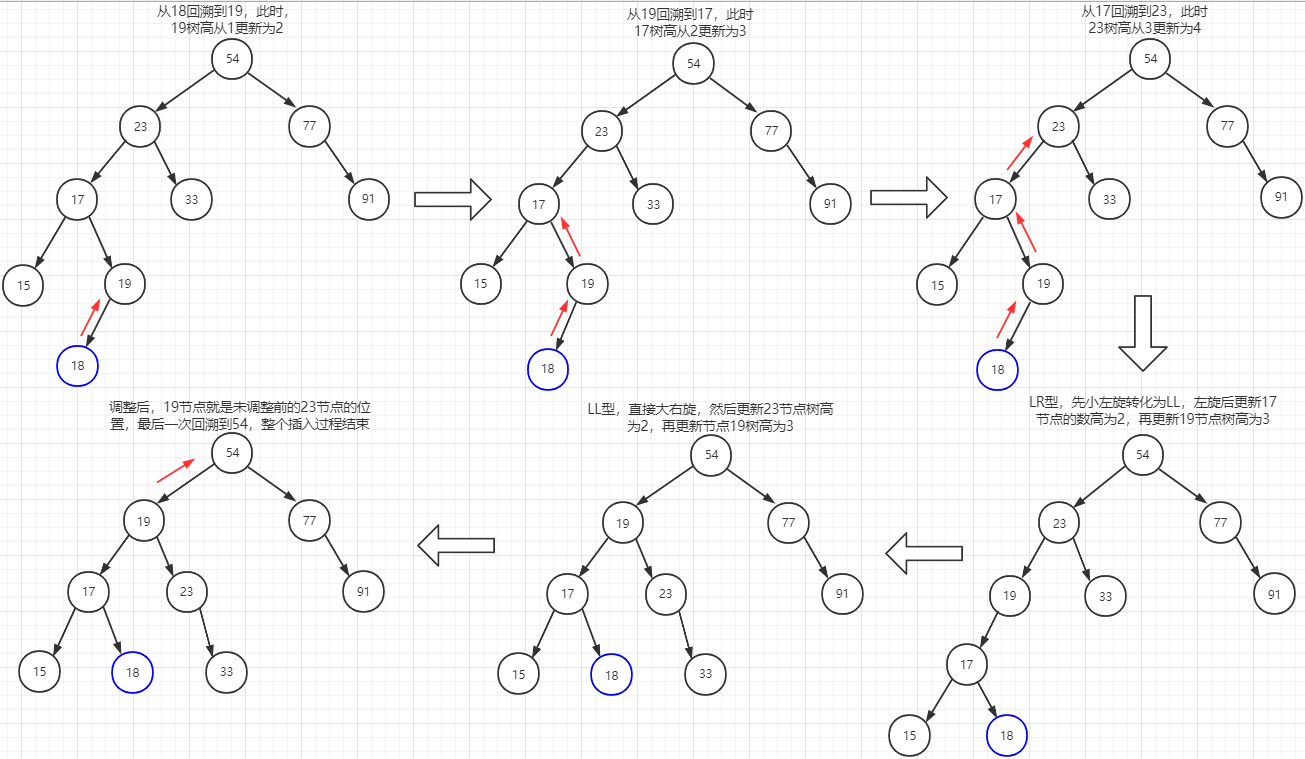
    image
    对于回溯，中间涉及到的失衡调整过程中，节点位置和节点高度的变化过程，我们这里先不细说，这只是为了大概模拟向下递归和向上回溯的过程，让我们脑海里右一个大概的流程。

    5.2. 4种调整情况分析

    这里，我们先介绍一下最小失衡二叉树的概念，在平衡二叉树中插入或删除一个结点后，从该结点起向上寻找第一个不平衡的结点（左右子树高度差大于1），以确定该树是否失衡。若找到，则以该结点为根的子树称为最小失衡子树。
    插入情况产生的最小失衡二叉树
    image
    删除情况产生的最小失衡二叉树
    image

    5.2.1 LL型

    发生失衡时，最小失衡二叉树的左子树高度大于右子树高度，且左子树的左子树高度也同样大于左子树的右子树高度。如下图：
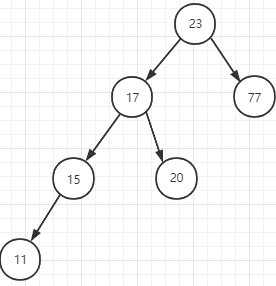
    image
    假设上图是一个AVL树的最小失衡二叉树，在根节点23发生失衡，其中左子树高度为3，大于右子树高度1，且23节点的左子树的左子树高度为2，大于23节点左子树的右子树高度1，这时候就是LL型，我们给出LL型的示例图，如下：
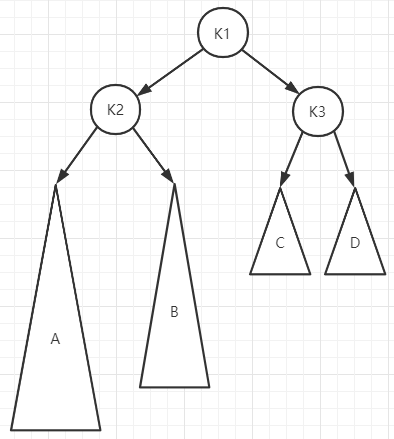
    image
    上图中，是LL型的最小失衡二叉树，其中A和B分别是最小失衡二叉树根节点左孩子节点的子树，C和D分别是最小失衡二叉树根节点右孩子节点的子树，我们这里来分析这四棵子树的高度之间的关系：
    假设A、B、C、D的高度分别为HA、HB、HC、HD，K2、K3的高度为HK2、HK3，由于是LL型失衡，故HK3 + 2 = HK2，而HK2 = HA + 1，HA = HB + 1，HK3 = max(HC, HD) + 1，故我们推出HA = HB + 1 = max(HC, HD) + 2。
    对于LL型失衡，我们从失衡的哪个节点开始，进行大右旋，就可以解决失衡，如图：
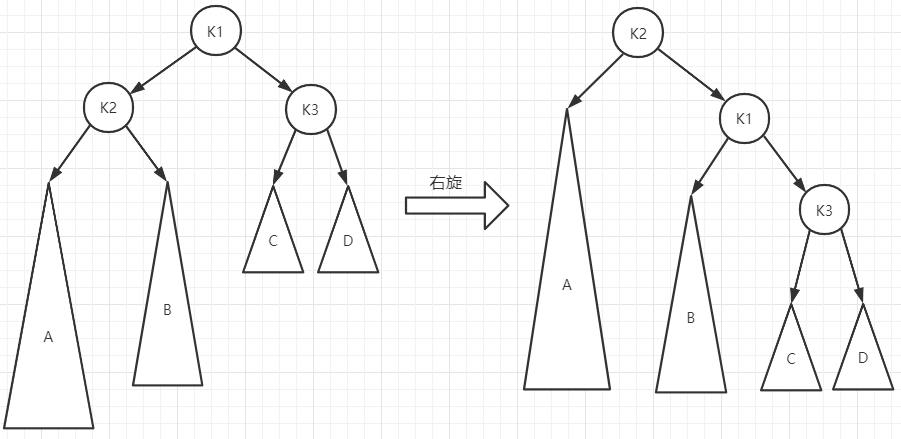
    image
    调整完之后，HA = HB + 1 = max(HC, HD) + 2这个等式依旧成立。但是这里需要注意的是，由于K1和K2节点的位置改变了，且K1节点变成了K2节点的子节点，所以我们需要在旋转完毕后先更新K1节点的高度，再更新K2节点的高度。

    5.2.1 LR型

    发生失衡时，最小失衡二叉树的左子树高度大于右子树高度，且左子树的右子树高度大于左子树的右子树高度。下面给出LR型的模型，如下图：
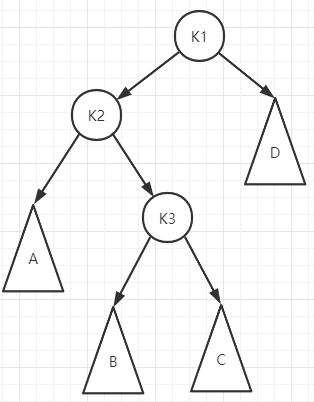
    image
    照例，我们来分析子树A、B、C、D之间高度的等式关系，由于是LR类型，所以对于K1节点来说，左子树高度和右子树高度的等式关系为：HK2 = HD + 2，且HK2 = max(HB， HC) + 2，HK3 = HA + 1，由上述等式，我们可以得出，HA = max(HB, HC) = HD。
    对于LR型失衡，我们先从失衡的节点的左节点进行一次小左旋，把它转化成LL型，再从失衡节点开始进行一次大右旋。如图
    小左旋
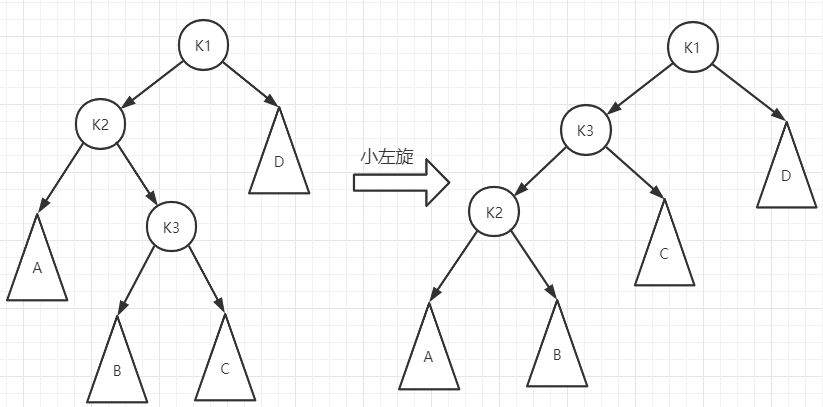
    image
    进行小左旋之后，我们可以明显看到这时候是LL型，故再来一次大右旋。
    大右旋
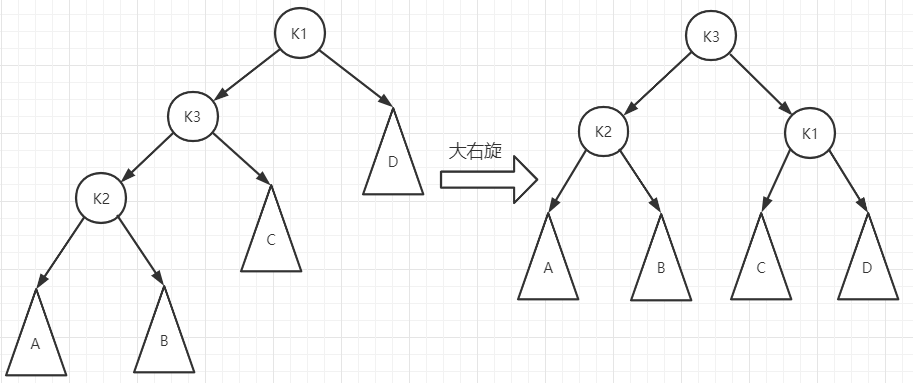
    image
    大右旋后，发现此时最小失衡二叉树已经平衡，且是一棵完美的平衡二叉树。

    5.2.3 RR型

    RR型的分析过程和LL型一样，只是旋转操作是镜像操作。

    5.2.4 RL型

    同理，RL型分析过程和LR一样，同样操作也是镜像操作。
    至此，我们已经分析完失衡调整的4中情况，可以进行代码设计。

    结构定义

    由于平衡二叉树是通过调整树高去维护平衡，所以我们必须在原来二叉排序树的结构定义加上树高的属性，则平衡二叉树的结构定义如下：

    struct Node {
	int key, h;
	Node *lchild, *rchild
};

    节点初始化

    Node *getNewNode(int key) {
    Node *p = new Node;
    p->key = key;
    p->h = 1;//由于插入时都是插入到叶子节点，所以高度为1
    p->lchild = p->rchild = NIL;
    return p;
}

    p->lchild = p->rchild = NIL中的NIL是一个虚拟叶子节点，是为了方便计算树高而定义出来的。

    NIL节点的定义

    另外我们还定义了一个NIL节点，表示虚拟叶子节点，是接在真正的叶子节点下面，这里定义NIL节点是为了更新高度好处理。

    Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL(void) {
    NIL->key = -1;
    NIL->lchild = NIL->rchild = NIL;
    NIL->h = 0;
    return ;
}

    这里，我们给出未带NIL节点和带NIL节点的图示
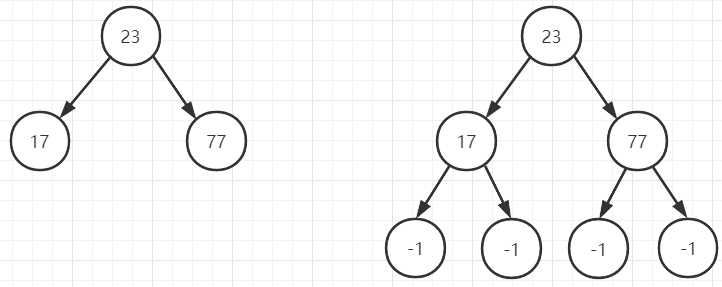
    image

    树高计算

    void update_height(Node *root) {
    root->h = max(root->lchild->h, root->rchild->h) + 1;
}

    在树高计算函数里，如果root参数是真实的叶子节点，且我们没有用定义NIL节点，则叶子节点的左右孩子节点都是NULL，这时候我们就不能通过访问孩子节点的高度来更新父节点的高度，除非做判空操作，非空才用子节点的树高更新父节点的树高。

    节点插入

    插入节点的操作更二叉排序树插入节点的操作相似，只是我们要多维护更新树高和失衡调整的操作，即在维护二叉排序树性质的同时，还要去维护平衡二叉树的性质。

    Node *insert(Node *root, int key) {
    if (root == NIL) {
        return getNewNode(key);
    }
    if (key == root->key) {
        return root;
    }
    if (key < root->key) {
        root->lchild = insert(root->lchild, key);
    } else {
        root->rchild = insert(root->rchild, key);
    }
    update_height(root);//插入完毕后，更新树高
    return maintain(root);//更新树高完毕后，才能去进行失衡调整的判断和失衡调整
}

    节点删除

    节点删除也是同理，在维护二叉树的性质的同时要维护平衡二叉树的性质。

    Node *erase(Node *root, int key) {
    if (root == NIL) {
        return NIL;
    }
    if (key < root->key) {
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key) {
        root->rchild = erase(root->rchild, key);
    } else {
        if (root->lchild == NIL && root->rchild == NIL) {
            delete root;
            return NIL;
        } else if (root->lchild == NIL || root->rchild == NIL) {
            Node *temp = root->lchild == NIL ? root->rchild : root->lchild;
            delete root;
            return temp;
        } else {
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    update_height(root);
    return maintain(root);
}

    失衡调整

    失衡调整函数主要分为两大部分：左右子树高度差判断，类型判断和处理。
    1.左右子树高度差判断：左右子树高度差小于2，则新插入节点后，还是平衡二叉树还是平衡状态，无需调整；左右子树高度差大于1，进行类型判断，并根据相应的类型进行调整处理。
    2.类型判断：
    LL型 大右旋
    LR型 小左旋 大右旋
    RL型 小右旋 大左旋
    RR型 大左旋

    Node *maintain(Node *root) {
	//根据高度差判断是否需要失衡跳帧
    if (abs(root->lchild->h - root->rchild->h) < 2) {
        return root;
    }
	//L型入口
    if (root->lchild->h > root->rchild->h) {
		//LR型入口
        if (root->lchild->rchild->h > root->lchild->lchild->h) {
			//小左旋
            root->lchild = left_rotate(root->lchild);
        }
		//LL LR型都需要大右旋
        root = right_rotate(root);
    }
	//R型入口
    if (root->rchild->h > root->lchild->h) {
		//RL型入口
        if (root->rchild->lchild->h > root->rchild->rchild->h) {
			//小右旋
            root->rchild = right_rotate(root->rchild);
        }
		//RR RL型都需要打左旋
        root = left_rotate(root);
    }
    return root;
}

    旋转操作

    左右旋操作都很简单，自己可以画图模拟，唯一需要注意的是旋转后要更新发生移动的节点的树高：
    1.对于左旋，旋转后原根节点变成了其右孩子的左节点，故我们需要更新原根节点（新根节点的左孩子）高度，再去更新新根节点的高度。
    2.对于左旋，旋转后原根节点变成了其左孩子的左节点，故我们需要更新原根节点（新根节点的右孩子）高度，再去更新新根节点的高度。

    左旋操作

    Node *left_rotate(Node *root) {
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    update_height(root);
    update_height(temp);
    return temp;
}

    右旋操作

    Node *right_rotate(Node *root) {
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    update_height(root);
    update_height(temp);
    return temp;
}

    输出函数

    这里我们采用先序遍历，但是修改输出函数的输出格式，先输出根节点的key值，在输出更节点的高度，在输出左右子树的key值。

    void output(Node *root) {
    if (root == NIL) {
        return ;
    }
    printf("(%d(%d) | %d, %d)
", root->key, root->h,
           root->lchild->key, root->rchild->key);
    output(root->lchild);
    output(root->rchild);
    return ;
}

    完整代码

    完整的代码我加上了调试信息，方便我们理解代码的失衡调整过程。

    /*************************************************************************
        > File Name: my_avl_tree.cpp
        > Author: ydqun
        > Mail: qq28*****5@163.com
        > Created Time: Wed 21 Apr 2021 05:41:39 PM CST
 ************************************************************************/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>

using namespace std;

struct Node {
    int key, h;
    Node *lchild, *rchild;
};

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL(void) {
    NIL->key = -1;
    NIL->lchild = NIL->rchild = NIL;
    NIL->h = 0;
    return ;
}

const char *maintain_str[] = {"", "LL", "LR", "RL", "RR"};

Node *getNewNode(int key) {
    Node *p = new Node;
    p->key = key;
    p->h = 1;//由于插入时都是插入到叶子节点，所以高度为1
    p->lchild = p->rchild = NIL;
    return p;
}

void update_height(Node *root) {
    root->h = max(root->lchild->h, root->rchild->h) + 1;
}

Node *left_rotate(Node *root) {
    printf("left_rotate: %d
", root->key);
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    update_height(root);
    update_height(temp);
    return temp;
}

Node *right_rotate(Node *root) {
    printf("right rotate: %d
", root->key);
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    update_height(root);
    update_height(temp);
    return temp;
}

Node *maintain(Node *root) {
    if (abs(root->lchild->h - root->rchild->h) < 2) {
        return root;
    }
    int maintain_type;
    if (root->lchild->h > root->rchild->h) {
        if (root->lchild->rchild->h > root->lchild->lchild->h) {
            root->lchild = left_rotate(root->lchild);
            maintain_type = 2;
        } else {
            maintain_type = 1;
        }
        root = right_rotate(root);
    }
    if (root->rchild->h > root->lchild->h) {
        if (root->rchild->lchild->h > root->rchild->rchild->h) {
            root->rchild = right_rotate(root->rchild);
            maintain_type = 3;
        } else {
            maintain_type = 4;
        }
        root = left_rotate(root);
    }
    printf("AVL Maintain: %s
", maintain_str[maintain_type]);
    return root;
}


Node *insert(Node *root, int key) {
    if (root == NIL) {
        return getNewNode(key);
    }
    if (key == root->key) {
        return root;
    }
    if (key < root->key) {
        root->lchild = insert(root->lchild, key);
    } else {
        root->rchild = insert(root->rchild, key);
    }
    update_height(root);
    return maintain(root);
}

Node *predecessor(Node *root) {
    Node *temp = root->lchild;
    while (temp->rchild != NIL) {
        temp = temp->rchild;
    }
    return temp;
}

Node *erase(Node *root, int key) {
    if (root == NIL) {
        return NIL;
    }
    if (key < root->key) {
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key) {
        root->rchild = erase(root->rchild, key);
    } else {
        if (root->lchild == NIL && root->rchild == NIL) {
            delete root;
            return NIL;
        } else if (root->lchild == NIL || root->rchild == NIL) {
            Node *temp = root->lchild == NIL ? root->rchild : root->lchild;
            delete root;
            return temp;
        } else {
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    update_height(root);
    return maintain(root);
}

void output(Node *root) {
    if (root == NIL) {
        return ;
    }
    printf("(%d(%d) | %d, %d)
", root->key, root->h,
           root->lchild->key, root->rchild->key);
    output(root->lchild);
    output(root->rchild);
    return ;
}


void clear(Node *root) {
    if (root == NIL) {
        return ;
    }
    clear(root->lchild);
    clear(root->rchild);
    delete root;
    return ;
}

void menu(void) {
    cout << "Please enter the operation: " << endl;
    printf("Please enter the operation: 
");
    printf("Press 1 to insert a node to avl tree
");
    printf("Press 2 to delete a node to avl tree
");
    printf("Press CTRL + D to quit!
");
}

int main() {
    int op, val;
    Node *root = NIL;
    while (scanf("%d", &op) != EOF) {
        if (op != 1 && op != 2) {
            printf("Please enter the right operation!
");
            continue;
        }
        printf("Enter the key you want to %s:
", op == 1 ? "insert" : "delete");
        scanf("%d", &val);
        switch (op) {
            case 1:
                root = insert(root, val);
            break;
            case 2:
                root = erase(root, val);
            break;
            default:
            break;
        }
        output(root);
        cout << endl;
    }
    return 0;
}

    测试

    ydqun@VM-0-9-ubuntu avl_tree % ./a.out                                                                                                                                                      [127]

1
Enter the key you want to insert:
56
(56(1) | -1, -1)

1
Enter the key you want to insert:
30
(56(2) | 30, -1)
(30(1) | -1, -1)

1
Enter the key you want to insert:
15
right rotate: 56
AVL Maintain: LL
(30(2) | 15, 56)
(15(1) | -1, -1)
(56(1) | -1, -1)

1
Enter the key you want to insert:
32
(30(3) | 15, 56)
(15(1) | -1, -1)
(56(2) | 32, -1)
(32(1) | -1, -1)

1
Enter the key you want to insert:
33
left_rotate: 32
right rotate: 56
AVL Maintain: LR
(30(3) | 15, 33)
(15(1) | -1, -1)
(33(2) | 32, 56)
(32(1) | -1, -1)
(56(1) | -1, -1)

2
Enter the key you want to delete:
30
left_rotate: 15
AVL Maintain: RR
(33(3) | 15, 56)
(15(2) | -1, 32)
(32(1) | -1, -1)
(56(1) | -1, -1)

1
Enter the key you want to insert:
78
(33(3) | 15, 56)
(15(2) | -1, 32)
(32(1) | -1, -1)
(56(2) | -1, 78)
(78(1) | -1, -1)

    原创博文，转发请加上原链接
  • 相关阅读:
    VSCode创建Vue项目完整教程
    npm安装vue，在vue/dist目录下没有产生vue.js文件 npm init y npm install vue@2
    技巧心得：DOS学习心得（一）
    c# winform 在新的应用程序域运行 wpf
    Vi下如何保存退出
    visio 文件VSD转jpg
    Too many open files的四种解决办法
    C# winform 窗体弹出选择目录或文件 的对话框
    https://gitee.com/antdesignblazor
    类型Microsoft.Office.Interop.Excel.ApplicationClass未定义构造函数
  • 原文地址：https://www.cnblogs.com/ydqblogs/p/14680857.html
Copyright © 2020-2023  润新知