二分专题

二分专题

二分专题从简到难，主要分为：朴素二分，特殊二分和二分答案，我们从这个难度顺序来介绍二分专题。

朴素二分

朴素二分是我们平时说的二分查找，使用二分查找的条件是查找的数组必须是有序的，例如。

在元素为10个的数组 [1, 3, 7, 9, 11, 23, 45, 67, 100, 108]查找出11，并输出它的下标，注意：下标从0开始计算。

输入：

首先输入一个N，表示一个数组的元素个数(3 < N <= 100)。
接着输入N个数据，数据是递增。
最后输入X，表示要查找的元素
例如：
10
1 3 7 9 11 23 45 67 100 108
67

输出

若查找的到，则输出x的下标，若查找不到，则输出-1
7

代码

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

int n, x, num[105];

int bs(int x) {
    int l = 0, r = n - 1, mid;
    while (l <= r) {
        mid = (l + r) / 2;
        if (num[mid] == x) {
            return mid;
        } else if (num[mid] < x) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return -1;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
    }
    cin >> x;
    cout << bs(x) << endl;
    return 0;
}

ydqun@VM-0-9-ubuntu bokeyuan % ./a.out                                                                                                                                                        [0]
10
1 3 7 9 11 23 45 67 100 108
67
7

运行过程

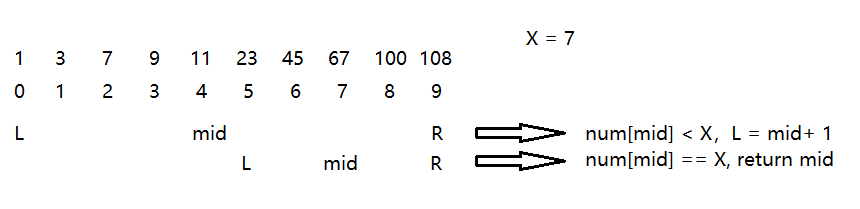
分析

二分查找每次都减少一半的查找范围，由此得到，查找的时间复杂度为 O（log(n)）

总结

二分查找	查找整型
while（）条件	l <= r
mid	(l + r) / 2或l + (r - l) / 2(防止溢出)
更新L	mid + 1
更新R	mid - 1

实战题目1

吃瓜群众

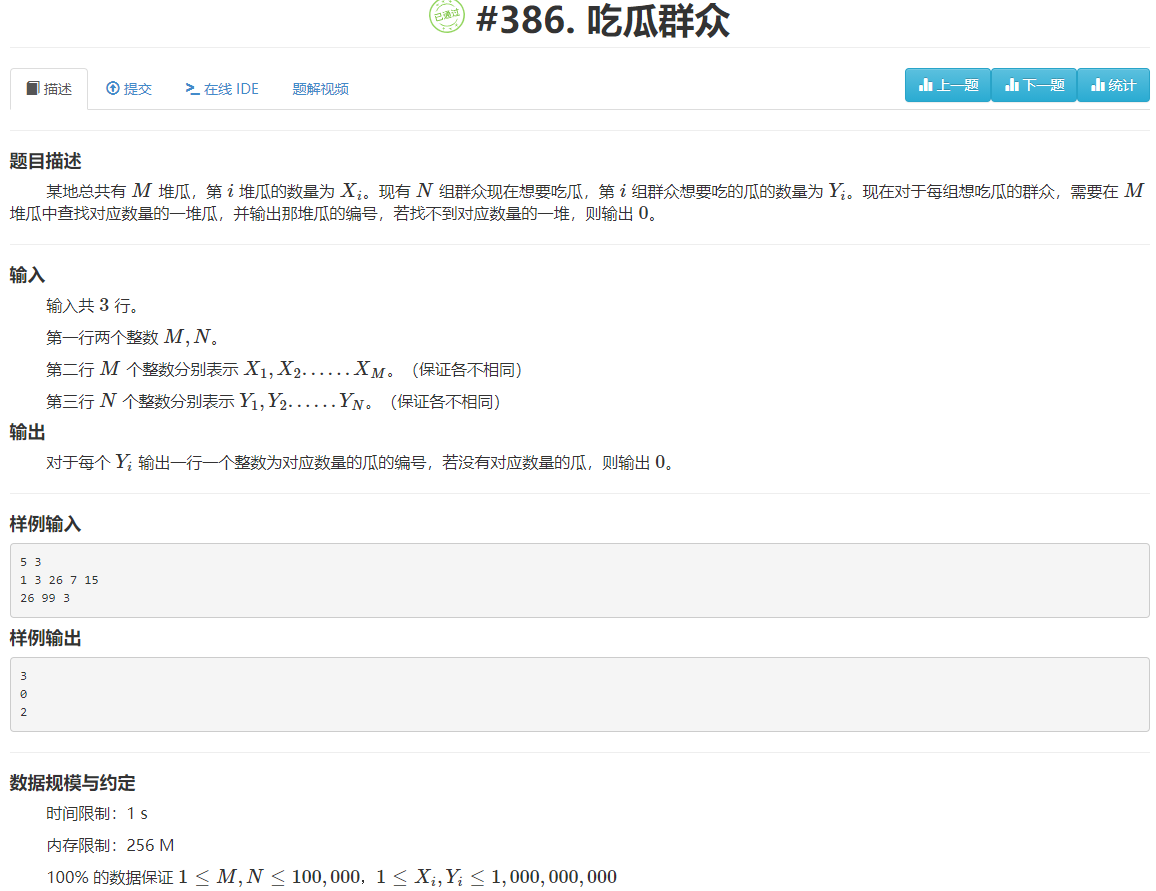
解前分析

解法1：

暴力求解，对于每一个群众的吃瓜数，都去与每队瓜里判断数目是否相等，但是本题N和M的数据最大到100000，暴力解法的时间复杂度为O（N*M），因为N和M相等，所以为O(N²)，程序运行起来大概率会超时。

解法2：

二分查找，我们可以先把瓜的堆号和瓜数结合成一个结构体，把所有所有瓜的结构体初始化成一个数组，在用C++的sort函数进行排序，然后对于每一个群众的吃瓜数，在瓜的数组中进行二分查找，返回查找到的结构体元素中的序号。由于sort排序的时间复杂度为O(nlog(n))，二分查找的时间复杂度为O(log(n))，M(M与N范围一样)个二分就O(nlog(n))，所以总时间复杂度为O(nlog(n))。

题解例程

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

struct node {
    int index, num;
};

bool cmp(const node &a, const node &b) {
    return a.num < b.num;
}

int n, m;
node gua[100005];

int binary_search(node *gua, int n, int target) {
    int l = 0, r = n - 1, mid;
    while (l <= r) {
        mid = (l + r) >> 1;
        if (gua[mid].num == target) {
            return gua[mid].index;
        } else if (gua[mid].num < target) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return 0;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i <= n - 1; i++) {
        scanf("%d", &gua[i].num);
        gua[i].index = i + 1;
    }
    sort(gua, gua + n, cmp);
    for (int i = 0; i < m; i++) {
        int target;
        scanf("%d", &target);
        printf("%d
", binary_search(gua, n, target));
    }
    return 0;
}

特殊二分

题目

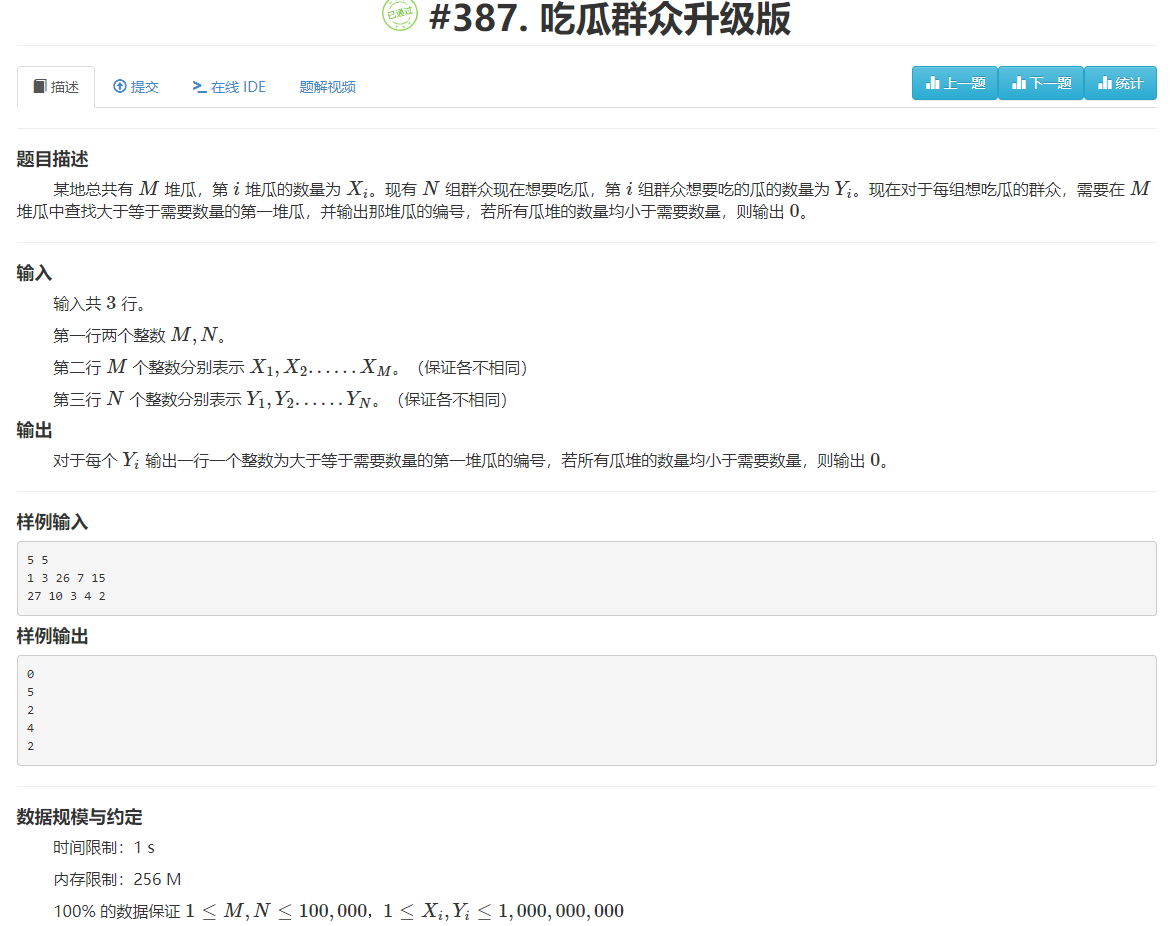
上一道吃瓜群众是找对与每个群众吃瓜数一样的瓜堆，而升级版的吃瓜群众是找出大于等于每个群众吃瓜数的第一个瓜堆，像这种问题，我们可以归类特殊二分范畴，这里我们先提出，特殊二分有两种类型，（1）找到第一个1（10型）；（2）找到最后一个1（01型），而吃瓜群众升级版是第一种类型。

分析（01特殊二分）

这里，有一句非常重要的话，二分的本质是筛选掉不包含答案的部分，然后再在包含答案的部分一直继续筛选。

解题例程

解法1

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

struct node {
    int cnt, num;
};

node wm[100005];
int n, m;

bool cmp(const node &a, const node &b) {
    return a.cnt < b.cnt;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i< n; i++) {
        scanf("%d", &wm[i].cnt);
        wm[i].num = i + 1;
    }
    sort(wm, wm + n, cmp);
    for (int i = 0; i < m; i++) {
        int t, l = 0, r = n - 1, mid;
        scanf("%d", &t);
        if (t > wm[n - 1].cnt) {
            printf("0
");
            continue;
        }
        while (l != r) {
            mid = (l + r) / 2;
            if (wm[mid].cnt >= t) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        printf("%d
", wm[l].num);
    }
    return 0;
}

运行测试

ydqun@VM-0-9-ubuntu 3 % g++ oj_387_v1.cpp                                                                                                                                                   [130]
ydqun@VM-0-9-ubuntu 3 % ./a.out                                                                                                                                                               [0]
5 5
1 3 26 7 15
27 10 3 4 2
0
5
2
4
2

这里，由于找不到符合吃瓜群众的瓜堆时，要输出-1，我们可以在输入每个群众的吃瓜数时判断是否大于所有瓜堆中的最大值，然后输出0；另外，我们也可以建立一个虚拟瓜堆，初始化该瓜堆一个极大值，且给该瓜堆标记为序号0，这样我们在所有真实的瓜堆中二分查找不到答案时，就会找到这个虚拟瓜堆，并输出序号0。这里，就是以下解法2。

解法2

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

struct node {
    int index, num;
};

int n, m;
node wm[100005];

bool cmp(const node &a, const node &b) {
    return a.num < b.num;
}

int bs (int target) {
    int l = 0, r = n, mid;
    while (l != r) {
        int mid = (l + r) / 2;
        if (wm[mid].num >= target) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return wm[l].index;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        scanf("%d", &wm[i].num);
        wm[i].index = i + 1;
    }
    sort(wm, wm + n, cmp);
    //建立虚拟瓜堆，由于所有瓜堆是升序的，所以我们必须把极大值的虚拟瓜堆放在最后一个位置
    wm[n].index = 0;
    wm[n].num = 210000000;
    int target;
    for (int i = 0; i < m; i++) {
        scanf("%d", &target);
        printf("%d
", bs(target));
    }
    return 0;
}

10型特殊二分

10特殊二分是找到第一个1。

二分答案

题目1

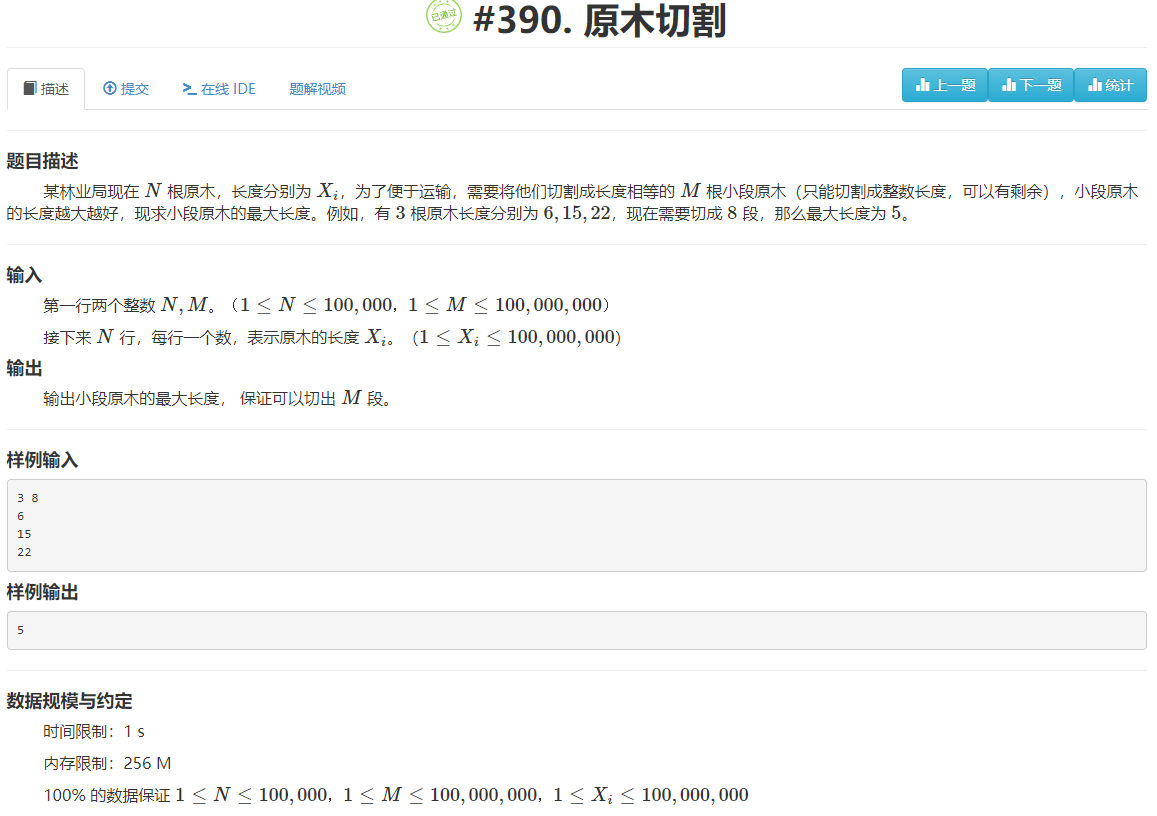
题目分析

像上述原木切割的题目，就是二分查找的拓展题目，二分答案，究竟什么是二分答案？我们可以来分析一下， 如下图。

现在，我们可以根据分析来写代码。

解题例程

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, m, lr, num[10005];
//根据切割长度求能够切割的小段原木段数
int func(int x) {
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        cnt += num[i] / x;
    }
    return cnt;
}

int bs(void) {
    int l = 1, r = lr;
    while (l != r) {
        int mid = (l + r + 1) / 2;//这里没有+1的话会出现死循环，可以尝试不+1模拟一下。
        int t = func(mid);
        if (t >= m) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
        lr = max(lr, num[i]);//lr存放为切割的最长的原木长度，确定切割的小段原木的最常长度
    }
    cout << bs() << endl;
    return 0;
}

题目2

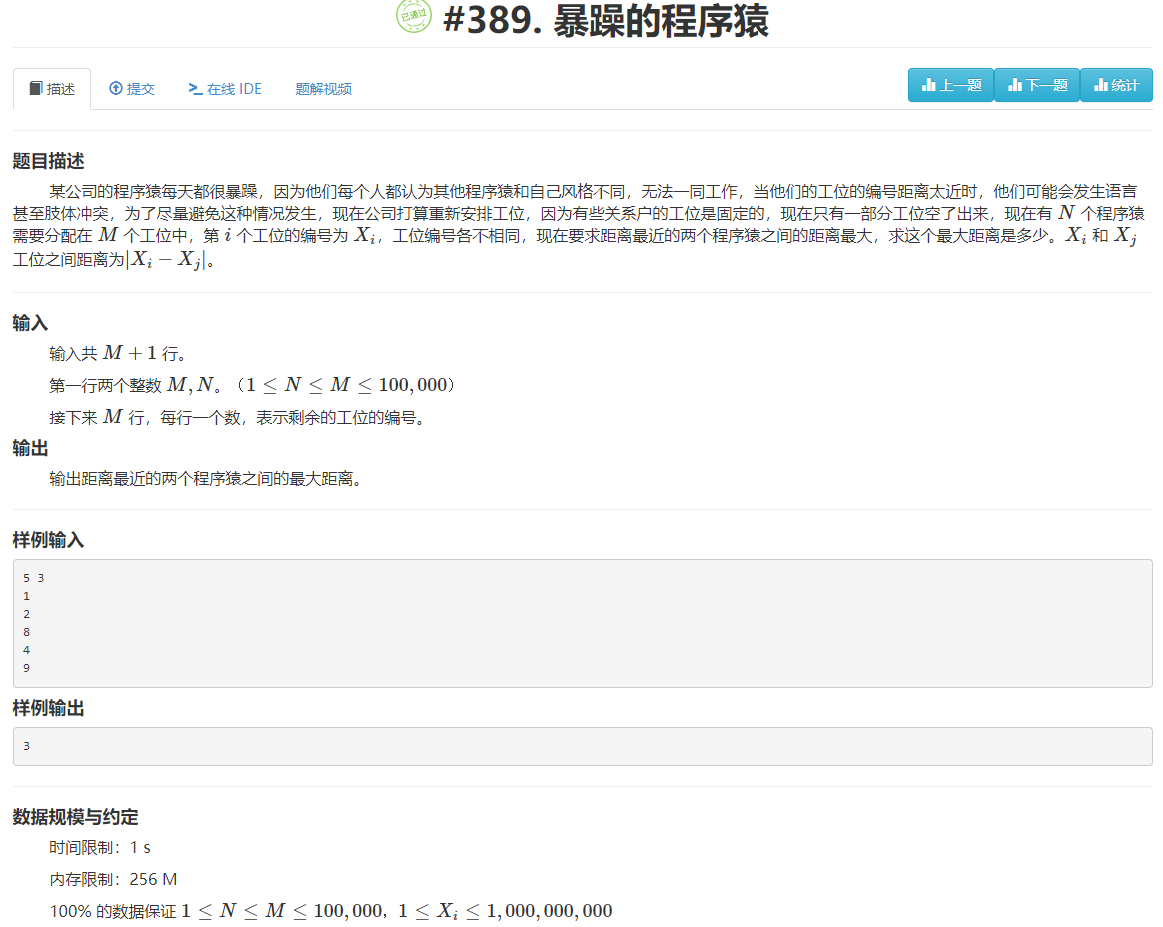
题目分析

像这种求“最小的最大”、“最近的最大”或“最大的最小”，“最远的最小”等问题，就是二分答案题目的关键字眼。

上述分析有一个关键点，根据距离X求安排的程序员人数S时，为了能够安排更多的程序员，我们应该从第一个位置开始安排一个程序员，之后根据座位距离大于等于距离X再继续安排程序员坐下，具体看代码。

解题代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, m, num[100005];
//根据距离X求能够安排的程序员人数
int func(int x) {
    //为了多安排程序员，我们第一个位置开始坐人，即体现在s从1开始计数，last为上一个程序员坐的位置
    int s = 1, last = num[0];
    for (int i = 1; i < n; i++) {
        if (num[i] - last >= x) {
            last = num[i];
            s++;
        }
    }
    return s;
}

int bs() {
    //l为距离最小值，r为距离最大值，最大值是安排两人坐在首尾位置时的情况
    int l = 1, r = num[n - 1] - num[0];
    while (l != r) {
        int mid = (l + r + 1) / 2;
        if (func(mid) >= m) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
    }
    sort(num, num + n);
    cout << bs() << endl;

    return 0;
}

编译并运行测试

ydqun@VM-0-9-ubuntu 3 % g++ my_oj_389.cpp                                                                                                                                                     [0]
ydqun@VM-0-9-ubuntu 3 % ./a.out                                                                                                                                                               [0]
5 3
1
2
8
4
9
3

题目3

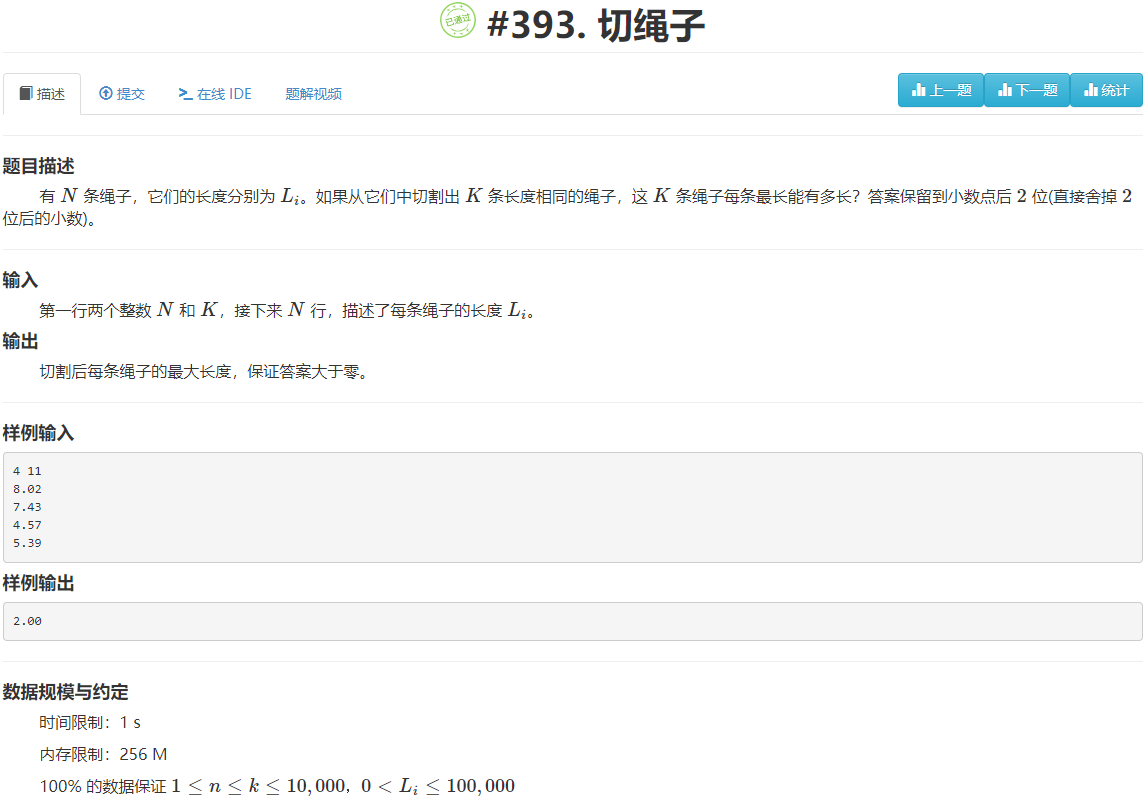
这道题目是浮点数的二分查找，这里有一个引申，
浮点数比较大小，由于精度问题，所以直接比较有时可能会出错。
所以在比较的时候需要用一个很小的数值来进行比较。当二者差小于这个很小的数时，就认为二者是相等的了。这个很小的数，称为精度。
精度由计算过程中需求而定。比如一个常用的精度为1E-6.也就是0.000001.
所以对于两个浮点数a,b，如果fabs(a-b)<=1E-6，那么就是相等了。
有了上述引申，我们可以开始分析浮点数的二分查找模型。

解题分析

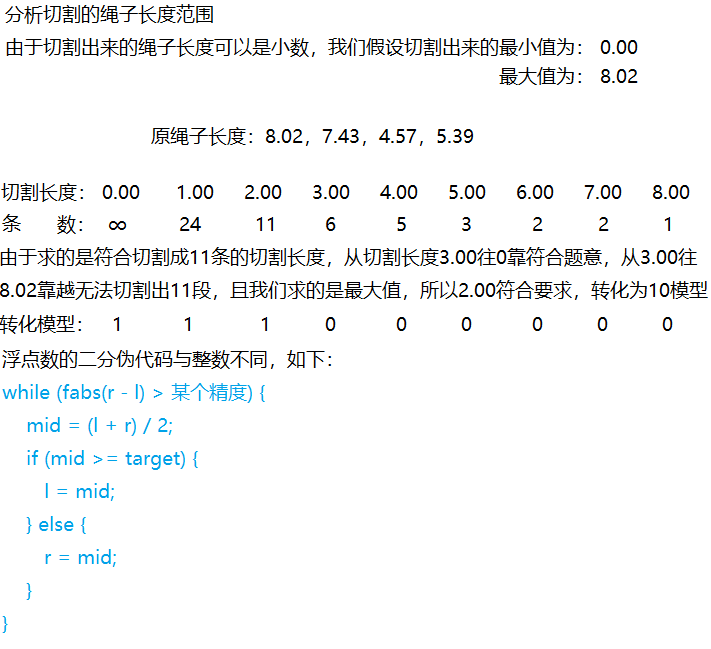
解题例程

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

int n, m;
double num[10005], mmax;

int func(double x) {
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        cnt += num[i] / x;
    }
    return cnt;
}

double bs() {
    double l = 0, r = mmax;
    while (fabs(r - l) > 0.0005) {
        double mid = (l + r) / 2;
        int s = func(mid);
        if (s >= m) {
            l = mid;
        } else {
            r = mid;
        }
    }
    return l;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        scanf("%lf", &num[i]);
        mmax = max(mmax, num[i]);
    }
    double ans = bs();
    //12.345 -> 乘以100并转化为整型，则为1234再除以100转为double，则为12.34，这样处理相当于只取小数点后两位（不四舍五入）
    double t1 = (int)(ans * 100) / 100.0;
    printf("%.2lf
", t1);
    return 0;
}

编译并运行

ydqun@VM-0-9-ubuntu 3 % ./a.out                                                                                                                                                                                                      [0]
4 11
8.02
7.43
4.57
5.39
2.00

题目4

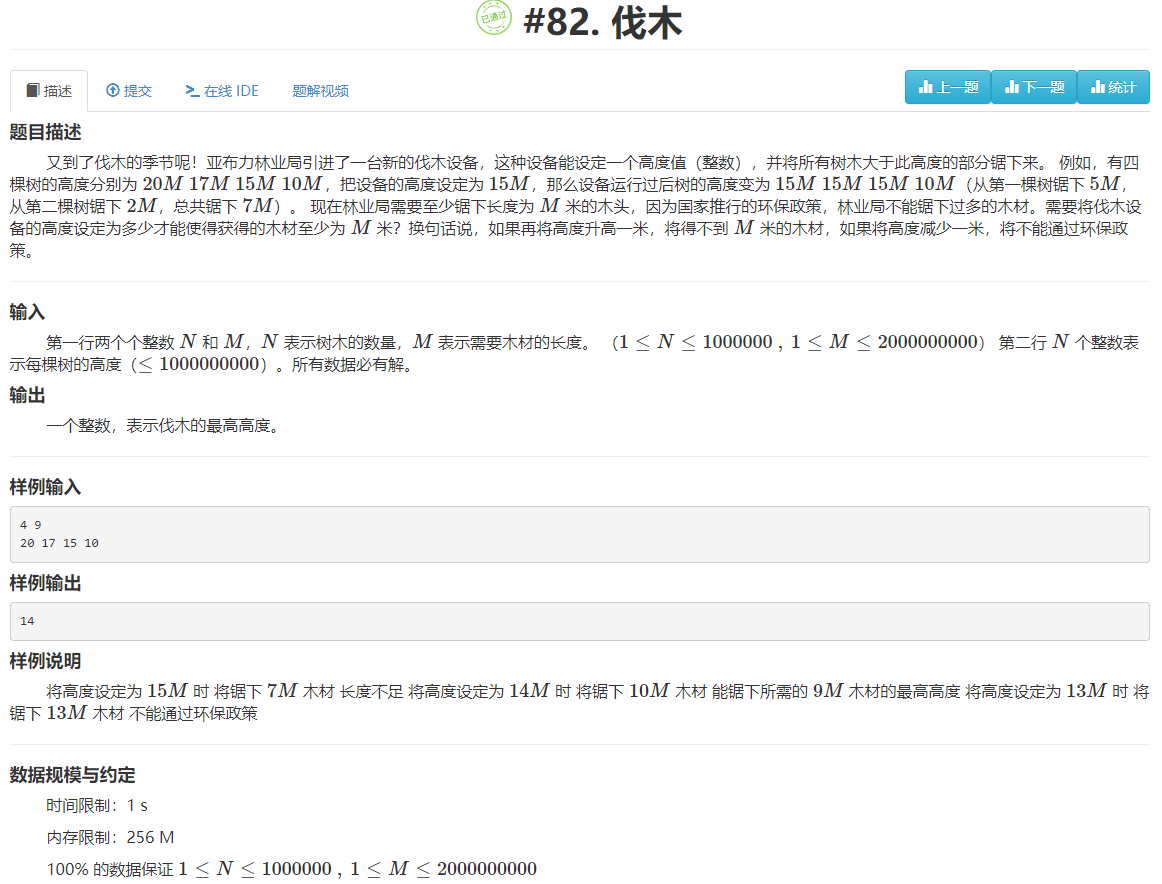
解题分析

需要注意的是，本题需要注意取值范围，由于每棵树的最高长度为1000000000，若把设备高度设置为0，且锯多棵树时，锯出来的木材长度超过int的取值范围，所以求出的锯出木材长度必须定义为long。

解题例程

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

int n, m, num[1000005], lr;
//根据设备设置高度x，求出据出来的木材长度
long func(int x) {
    long cnt = 0;
    for (int i= 0; i < n; i++) {
        if (num[i] > x) {
            cnt += (num[i] - x);
        }
    }
    return cnt;
}

int bs() {
    int l = 0, r = lr;
    while (l != r) {
        int mid = (l + r + 1) / 2;
        if (func(mid) >= m) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
        lr = max(lr, num[i]);
    }
    cout << bs() << endl;
    return 0;
}

题目5

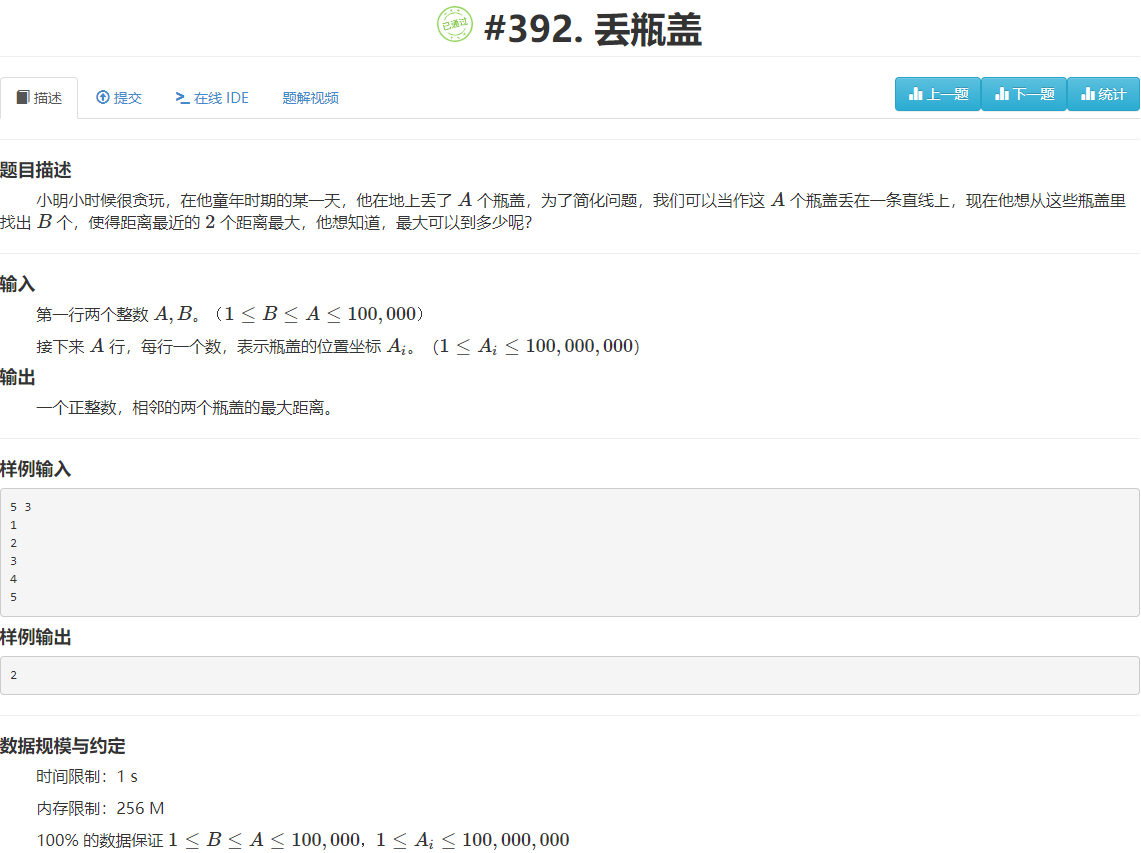
题目分析

例程

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, m, num[10005];

int func(int x) {
    int t = 1, last = num[0];
    for (int i = 1; i < n; i++) {
        if (num[i] - last >= x) {
            t++;
            last = num[i];
        }
    }
    return t;
}

int bs() {
    int l = 1, r = num[n - 1] - num[0];
    while (l != r) {
        int mid = (l + r + 1) / 2;
        if (func(mid) >= m) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
    }
    sort(num, num + n);
    cout << bs() << endl;
    return 0;
}