数据结构-图

图的概念

图的基础概念

图的结构很简单，就是节点集V和边集E的合并，可表示为G = (V, E)；

图的方向

图分为有向图和无向图。
有向图即点和点之间的边是有方向的，该边是有箭头标明方向，如下图

上图中，我们可以举例，有一条边为1->2，若反过来说有一条边2->1则为错误，因为箭头已经标明了方向。

无向图即点和点之间的边是没有方向的，该边没有箭头标明方向如下图

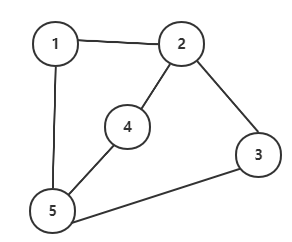
上图中，我们可以节点1和节点2之间有一条无向边，即1-2和2-1是同一条边。

加权图和无权图

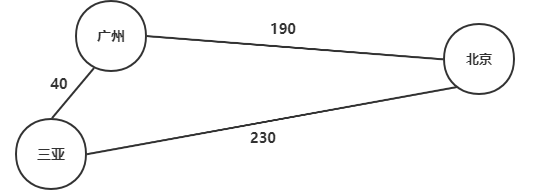
加权图，即边是有权值的，比如联合到我们实际生活，若我们用一张表来表示中国城市之间的距离，那么三亚到广州，三亚到北京的距离是不同的，所以我们需要赋予边一个权值属性，如下图：

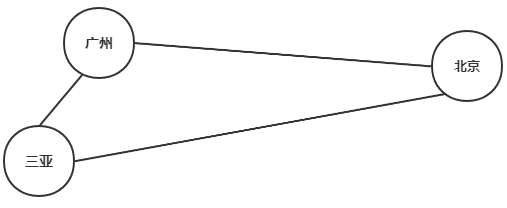
无权图，也叫等权图，即图的每条边都没有权值（或者权值为1），假如我们用一张表来表示中国各个城市之间是否有直通的高铁，则我们可以用无权图来表示，若两个城市之间有边，则说明两个城市之间有高铁。

需要注意的是:

1. 无权图的每条表的权值我们一般约定为1，而不是说每一条边都没有权值，故无权图也叫等权图。
2. 边的权值可以为负数。

路径与环

路径

一次遍历节点序列之间的边所形成的轨迹，注意，依次意味着有序，如图1->2->4->3就是一条路径

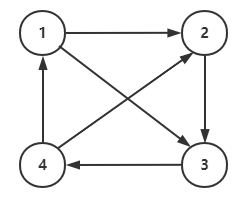
环

一条路径包含相同的节点两次或者两次以上，例如上图中1->2->4->3->1或者1->4->3->1就是环。
这里特别说明一下负权环这种情况，由于边的权值可以为负数，所以当跑完一个环后，总的权值是负数，这该环是负权环，如下图中1->2->3->4->1就是一个负环：