入手点是每段路程中能量$e$与时间$t$的关系,$t-e$这个函数的导数对于各个路段一样,否则我们可以从导数大的一段路抽出一部分能量分给导数小的,这样会更优
毕姥爷在考场上的做法:猜一猜,然后拿python打打表,发现确实是这样的
那么可以把$e/t$化成关于每段速度$v$的一个式子
$e/t$
$=(ks(v-v')^2)/(s/v)$
针对$v$求导
$=k(v-v')/(1/v^2)$
$=kv^2(v-v')$
然后二分这个导数$d$,尝试反解出$v$
$kv^2(v-v')=d$
$v^2(v-v')=d/k$
$v^3-v^2v'-d/k=0$
不幸的是这个东西一点也不好解,所幸$v$大于零,所以这个函数大概长这样↓
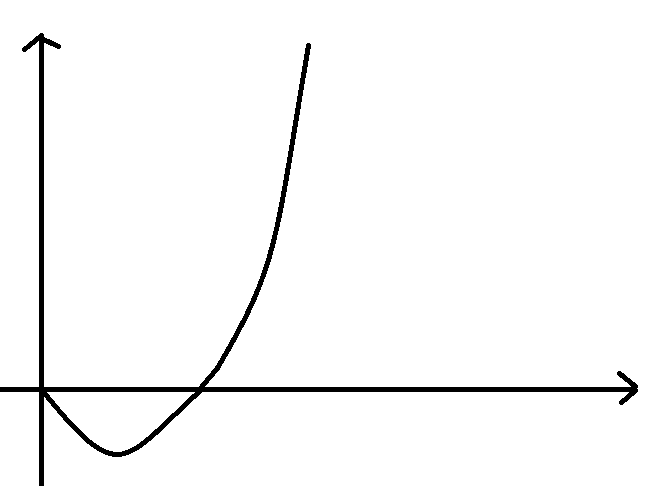
那么这个零点是可以二分出来的,所以再二分一次就好了

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=10005; 6 int n; double e,ans,s[N],k[N],v[N]; 7 double V(double der,int idx) 8 { 9 double l=0,r=1e9; 10 for(int i=1;i<=80;i++) 11 { 12 double mid=(l+r)/2; 13 if(mid*mid*mid-mid*mid*v[idx]>=der/k[idx]) r=mid; 14 else l=mid; 15 } 16 return r; 17 } 18 double Energy(double x) 19 { 20 double ret=0; 21 for(int i=1;i<=n;i++) 22 ret+=s[i]*(V(x,i)-v[i])*(V(x,i)-v[i])*k[i]; 23 return ret; 24 } 25 int main() 26 { 27 scanf("%d%lf",&n,&e); 28 for(int i=1;i<=n;i++) 29 scanf("%lf%lf%lf",&s[i],&k[i],&v[i]); 30 double l=0,r=1e9; 31 for(int i=1;i<=80;i++) 32 { 33 double mid=(l+r)/2; 34 (Energy(mid)>e)?r=mid:l=mid; 35 } 36 for(int i=1;i<=n;i++) ans+=s[i]/V(l,i); 37 printf("%f",ans); 38 /* double vv[4]={0,5.12939919,8.03515481,6.17837967}; 39 for(int i=1;i<=n;i++) 40 { 41 double t=s[i]/vv[i]; 42 double g=k[i]*(vv[i]-v[i])*(vv[i]-v[i])*s[i]; 43 printf("%lf %lf %lf ",t,g,vv[i]*vv[i]*(vv[i]-v[i])*k[i]); 44 }*/ 45 return 0; 46 }
