一句话:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降求解参数,来达到将数据二分类的目的。
假设函数
逻辑回归算法是将线性函数的结果映射到 sigmoid 函数中:
[h_{ heta}{(x)}=frac{1}{1+e^{-z}}=frac{1}{1+e^{ heta^{T}x}}
]
函数的形式如下:
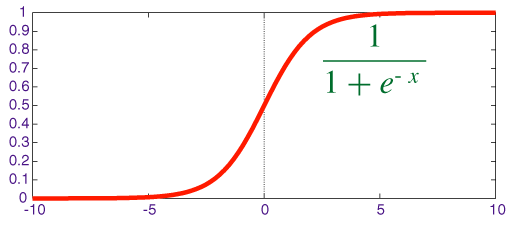
因此对于输入 x 分类结果为类别 1 和类别 0 的概率分别为:
[egin{align}
P(y=1|x; heta)&=h_{ heta}{(x)}\
P(y=0|x; heta)&=1-h_{ heta}(x)
end{align}
]
极大似然估计
利用极大似然估计的方法求解损失函数,首先得到概率函数为:
[P(y|x; heta)=(h_{ heta}(x))^y*(1-h_{ heta}{(x)})^{1-y}
]
因为样本数据互相独立,所以它们的联合分布可以表示为各边际分布的乘积,取似然函数为:
[egin{align}
L( heta)&=prod_{i=1}^{m}{P(y^{(i)}|x^{(i)}; heta)}\
&=prod_{i=1}^{m}{(h_{ heta}(x^{(i)}))^{y^{(i)}}*(1-h_{ heta}(x^{(i)}))^{1-y^{(i)}})}
end{align}
]
取对数似然函数:
[l( heta)=log(L( heta))=sum_{i=1}^{m}{(y^{(i)}log{(h_{ heta}(x^{(i)}))}+(1-y^{(i)})log({1-h_{ heta}{(x^{(i)})}}))}
]
最大似然估计就是要求得使 (l( heta)) 取最大值时的 ( heta) ,为了应用梯度下降法。我们稍微变换一下:
[J( heta)=-frac{1}{m}l( heta)
]
为什么使用极大似然函数来作为损失函数?
- 对损失函数求负梯度之后,参数的更新只与 (x_j^i) 和 (y^i) 相关,和
sigmoid函数本身的梯度是无关的; - 从损失函数的函数图形来分析:
对于单个样本来讲,(J( heta)) 所对应的 (C( heta)) 为:
[C( heta)=-[ylog{h_{ heta}(x)}+(1-y)log{(1-h_{ heta}(x))}]
]
当 (y=1) 时:(C( heta)=-log{h_{ heta}(x)})
其函数图像为:
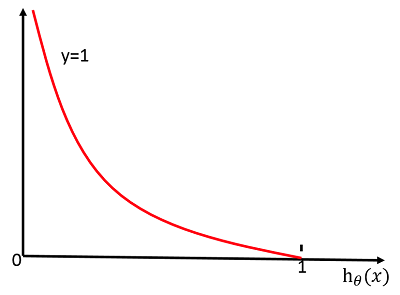
从图中可以看出,对于正类 (y=1),当预测值 (h_{ heta}(x)=1) 时,损失函数 (C( heta)) 的值为 0,这正是我们希望得到的。反之,则会给学习算法较大的惩罚。
当 (y=0) 时:(C( heta)=-log{(1-h_{ heta}(x))})
其函数图像为:
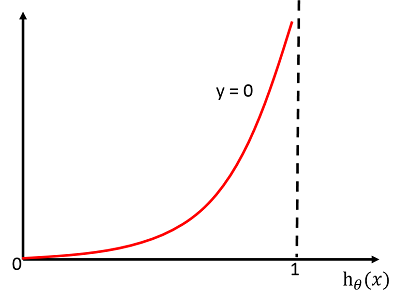
分析同上。
存在的缺点
- 准确率不是很高,因为形式比较简单,很难去拟合数据的真实分布;
- 很难处理数据不平衡的问题,比如正负样本比为 10000:1 时,把所有的样本都预测为正,也能使损失函数的值比较小;
- 处理非线性数据较麻烦
- 逻辑回归本身无法筛选特征。有时候用 GBDT 来筛选特征,然后再用逻辑回归。