基本信息
论文题目:GRAPH ATTENTION NETWORKS
时间:2018
期刊:ICLR
主要动机
探讨图谱(Graph)作为输入的情况下如何用深度学习完成分类、预测等问题;通过堆叠这种层(层中的顶点会注意邻居的特征),我们可以给邻居中的顶点指定不同的权重,不需要任何一种耗时的矩阵操作(比如求逆)或依赖图结构的先验知识。
CNN 结构可以有效用于解决网格状的结构数据,例如图像分类等。但是现有的许多任务的数据并不能表示为网格状的结构,而是分布在不规则的区域,如社交网络、生物网络等。这样的数据通常用图的形式来表示。
目前有些研究通过扩展神经网络来处理不规则结构图,包括循环神经网络(RNN)、图神经网络(GNN)及其改进的模型。另一种研究思路是把卷积泛化到图域中,分为谱方法和非谱方法两种。
注意力机制的一个好处是可以处理可变大小的输入,并且关注输入的最相关部分以做出决策。当注意机制用于计算单个序列的表示时,通常将其称为自注意或内注意。该机制和 RNN 结合已经广泛应用于机器阅读、句子表示和机器翻译领域。
作者提出了一种基于注意机制的架构,能够完成图结构数据的节点分类。该方法的思路是通过注意其邻居节点,计算图中的每个节点的隐藏表征,还带有自注意策略。这种架构有多重性质:
- 运算高效,因为它可以在 “顶点 - 邻居” 对上并行计算;
- 可以通过对近邻节点指定任意的权重应用于不同度的图节点;
- 该模型直接适用于归纳学习问题,其中包括需要将模型泛化为此前为见的图的任务。
GAT 架构
单个 graph attentional layer 的输入是一个节点特征向量集合,(h=lbrace vec{h_1},vec{h_2},dots,vec{h_N} brace,; vec{h_i}in R^F),其中 (N) 表示节点的数目,(F) 表示每个节点的特征的数目。并生成一个新的节点特征集合 (h^{'}=lbrace vec{h_1^{'}},vec{h_2^{'}},dots,vec{h_N^{'}} brace,; vec{h_i^{'}}in R^{F^{'}}) 作为输出,其中 (F) 和 (F^{'}) 具有不同的维度。
为了获得足够的表达能力以将输入特征变换为更高级别的特征,需要至少一个可学习的线性变换。为此,作为初始步骤,一个共享的线性变换参数矩阵 (Win R^{F^{'} imes F}) 被应用于每一个节点。然后执行 self-attention 处理:
其中,(a) 是一个 (R^{F^{'}} imes R^{F^{'}} o R) 的映射,公式(1)表示了节点 (j) 的特征对于节点 (i) 的重要性。一般来说,self-attention 会将注意力分配到图中所有的节点上,这种做法显然会丢失结构信息。为了解决这一问题,作者使用了一种 masked attention 的方法 -- 仅将注意力分配到节点 (i) 的邻居节点集上,即 (N_i),其中节点 (i) 也包括在 (N_i) 中。为了使系数在不同节点之间易于比较,我们使用 softmax 函数在 (j) 的所有选择中对它们进行标准化:
注意力机制 (a) 是一个单层前馈神经网络,其中 (vec{a}in R^{2F^{'}}) 是权重参数,使用 LeakyReLU 作为激活函数。完全展开后,由注意机制计算的系数可以表示为:
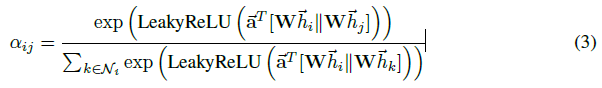
归一化的注意力系数用于计算与它们对应的特征的线性组合,以用作每个节点的最终输出特征,采用非线性的函数:
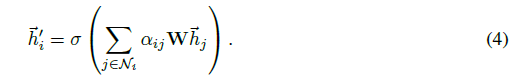
为了提高模型的拟合能力,在本文中还引入了多抽头的 self-attention(如图 1 右侧部分。与《Attention is All You Need》一致),即同时使用多个 (W^k) 计算 self-attention,然后将各个计算得到的结果进行合并(连接或求和):
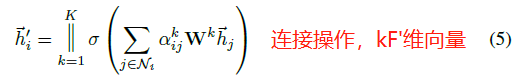
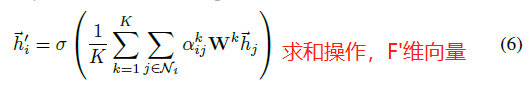
模型比较
上一节描述的图注意力层直接解决了之前在图结构上使用神经网络建模的方法的几个问题:
- 计算高效:self-attention 层的操作可以在所有的边上并行,输出特征的计算可以在所有顶点上并行。没有耗时的特征值分解。单层的 GAT 的时间复杂度为 (O(|V|FF^{'}+|E|F^{'})) 。尽管 multi-head 注意力将存储和参数要求乘以系数 K,但是单个 head 的计算完全独立且可以并行化。
- 与 GCN 相反,我们的模型允许(隐式)为同一邻域的节点分配不同的重要性,从而实现模型表示能力的飞跃;
- 对于图中的所有边,attention 机制是共享的。因此 GAT 也是一种局部模型。也就是说,在使用 GAT 时,我们无需访问整个图,而只需要访问所关注节点的邻节点即可。这一特点的作用主要有:(1)可以处理有向图(若 (j o i) 不存在,仅需忽略 (alpha_{ij}) 即可);(2)可以被直接用于进行归纳学习。
- 最新的归纳学习方法(GraphSAGE 2017)通过从每个节点的邻居中抽取固定数量的节点,从而保证其计算的一致性。这意味着,在执行推断时,我们无法访问所有的邻居。然而,本文所提出的模型是建立在所有邻节点上的,而且无需假设任何节点顺序。
我们能够生成一个利用稀疏矩阵运算的 GAT 层版本,将存储复杂性降低到节点和边缘数量的线性,并在较大的图形数据集上实现 GAT 模型。然而,我们使用的张量操作框架仅支持秩 - 2 张量的稀疏矩阵乘法,这限制了当前实现的层的批处理能力(特别是对于具有多个图的数据集),适当地解决这一限制是未来工作的重要方向。根据现有图形结构的规律性,在稀疏场景中,GPU 相比于 CPU 可能无法提供主要的性能优势。
实验评估
归纳学习(Inductive Learning):先从训练样本中学习到一定的模式,然后利用其对测试样本进行预测(即首先从特殊到一般,然后再从一般到特殊),这类模型如常见的贝叶斯模型。
演绎学习(Transductive Learning):先观察特定的训练样本,然后对特定的测试样本做出预测(从特殊到特殊),这类模型如 k 近邻、SVM 等。
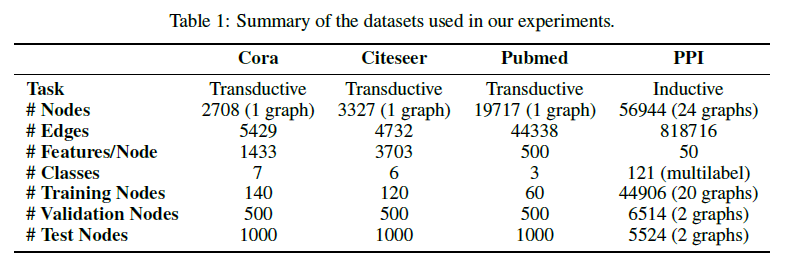
在演绎学习中使用三个标准的引证网络数据集——Cora、Citeseer 与 Pubmed。在这些数据集中,节点对应于文档,边(无向的)对应于引用关系。节点特征对应于文档的 Bag of Words 表示。每个节点拥有一个类别标签(在分类时使用 softmax 激活函数)。每个数据集的详细信息如下表所示:
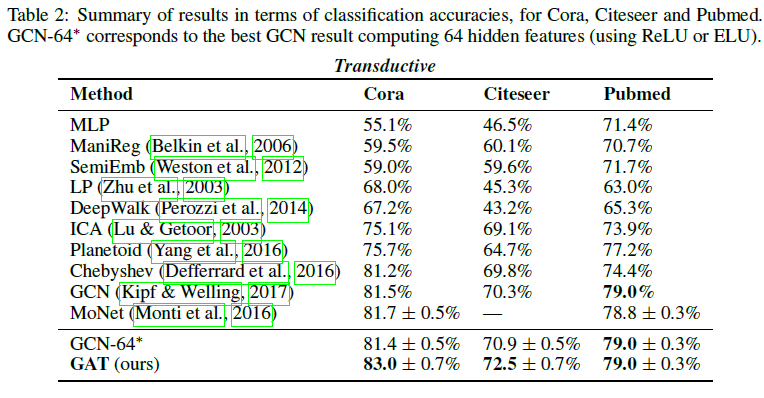
演绎学习的实验结果如下表所示,可以看到,GAT 模型的效果要基本优于其他模型:
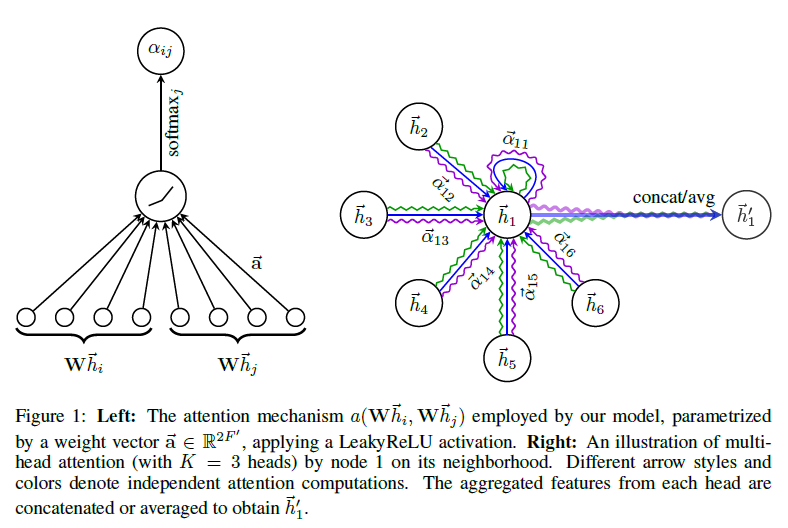
对于归纳学习,本文使用了一个蛋白质关联数据集(protein-protein interaction, PPI),在其中,每张图对应于人类的不同组织。此时,使用 20 张图进行训练,2 张图进行验证,2 张图用于测试。每个节点可能的标签数为 121 个,而且,每个节点可以同时拥有多个标签(在分类时使用 sigmoid 激活函数),其实验结果如下: