本蒟蒻参加了今年的NOIP2018普及组的初赛
感觉要凉
总而言之,今年的题要说完全没有难度倒也不至于,还有不少拼RP的题,比如第一次问题求解考逻辑推理,第一次完善程序考双链表等
下面我就和大家一起看看
声明:题目答案是我和同时考试的同学们一起做出来的,不保证正确性,不确定的会在之前加*
更新:标准答案出来了,答案不会有误
2018.10.14更新:充实选择题内容
如有错误欢迎指正
一、单项选择题
1、以下哪一种设备属于输出设备:()
A 扫描仪 B 键盘 C 鼠标 D 打印机
答案:D
打印机(Printer) 是计算机的输出设备之一,用于将计算机处理结果打印在相关介质上。
2、下列四个不同进制的数中,与其他三项数值上不相等的是()
A \((269)_{16}\)
B \((617)_{10}\)
C \((1151)_{8}\)
D \((1001101011)_{2}\)
答案:D
可以全转十进制计算,也可以像我在考场上那样转2进制:
\((269)_{16}=(1001101001)_2\)
\((617)_{10}=(1001101001)_2\)
\((1151)_8=(1001101001)_2\)
十进制转二进制:
短除之后倒取余数

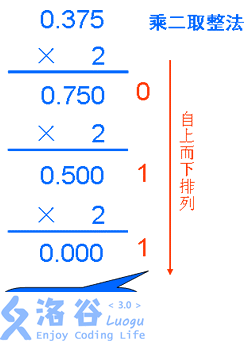
十六进制转二进制:
把16进制的每一位展开成4位二进制数,位数不足的补0,连起来后去掉前导0

(这个图忘裁剪了)
八进制、四进制分别转成3位、2位二进制数,道理和十六进制一样
3、\(1\)MB等于()
A \(1000\)字节
B \(1024\)字节
C \(1000*1000\)字节
D \(1024*1024\)字节
答案:D
\(1MB\)=\(1024KB\)=\(1024*1024B\)
4、广域网的英文缩写是()
A LAN
B WAN
C MAN
D LNA
答案:B
广域网(WAN,Wide Area Network)也称远程网(long haul network )。通常跨接很大的物理范围,所覆盖的范围从几十公里到几千公里,它能连接多个城市或国家,或横跨几个洲并能提供远距离通信,形成国际性的远程网络。
另外还有
局域网(Local Area Network,LAN)是指在某一区域内由多台计算机互联成的计算机组。一般是方圆几千米以内。局域网可以实现文件管理、应用软件共享、打印机共享、工作组内的日程安排、电子邮件和传真通信服务等功能。
城域网(Metropolitan Area Network)是在一个城市范围内所建立的计算机通信网,简称MAN。属宽带局域网。
LNA(低噪声放大器)
LNA即低噪声放大器,是噪声系数很低的放大器。一般用作各类无线电接收机的高频或中频前置放大器(比如手机、电脑或者iPAD里面的WiFi),以及高灵敏度电子探测设备的放大电路。
5、中国计算机协会与()年创办全国青少年计算机程序设计竞赛。
A 1983
B 1984
C 1985
D 1986
答案:B
1984年,教育部和中国科协委托中国计算机学会举办了全国青少年计算机程序设计竞赛,即全国青少年信息学奥林匹克竞赛
这种题做对只能拼RP,看来我RP不够
6、如果开始时计算机处于小写输入状态,现在有一只小老鼠反复按照CapsLock、字母键A、字母键S、字母键D、字母键F的顺序循环按键,即CapsLock、A、S、D、F、CapsLock、A、S、D、F、……、屏幕上输出的第81个字母是字母()。
A. A B. S C.D D.a
答案:A
周期为A,S,D,F,a,s,d,f,长度为8
80模10等于1,周期的第一个数即为A
7、根节点深度为0,一棵深度为h的满K叉树,即除最后一层无任何子节点外,每一层上所有节点都有k个子节点的树,共有()个节点。
A \((k^{h+1}-1)/(k-1)\)
B \(k^{h-1}\)
C \(k^h\)
D \((k^{h-1})/(k-1)\)
答案:A
第一版我是这么写的:
这个自己随便代个数进去就出来了,严谨证明的话自行百度
其实我不会证明
好不负责啊
真的可以打表找规律
但这事实上是等比数列求和:
第0层的节点为1,第1层为\(k\),第二层为\(k^2\),直到第h层为\(k^2\)。
则节点数为:
\(1+k^1+k^2+k^3+...+k^h=\frac{1-k^{h+1}}{1-k}\)
即 \(\frac{k^{h+1}-1}{k-1}\)
8、以下排序算法中,不需要进行关键字比较操作的算法是()。
A 基数排序
B 冒泡排序
C 堆排序
D 直接插入排序
答案:A
后三个排序都是基于比较的排序算法(复杂度分别为\(O(n^2)\),\(O(n logn)\),\(O(n^2)\))
基数排序是通过键值的资讯来分组处理的,大概长这样:
设原数列为73, 22, 93, 43, 55, 14, 28, 65, 39, 81
按他们的个位把他们装进对应的桶中:
0
1 81
2 22
3 73 93 43
4 14
5 55 65
6
7
8 28
9 39
重新串接,得:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
再按照十位数装桶:
0
1 14
2 22 28
3 39
4 43
5 55
6 65
7 73
8 81
9 93
再次串接,得:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
这时排序完毕
复杂度:\(O(d(n+radix))\)
\(d\)为关键码的个数,\(radix\)为关键码的取值范围
关于排序算法还有时间复杂度和稳定性的问题,也很重要,说不定明年就会考呢
9、给定一个含N个不相同数字的数组,在最坏情况下,找出期中最大或最小的树,至少需要N-1此操作。则最坏情况下,在该数组中同时找最大与最小的数至少需要()次操作。(\(\lceil\rceil\)表示向上取整,\(\lfloor\rfloor\)表示向下取整)
A \(\lceil3N/2\rceil-2\)
B \(\lfloor3N/2\rfloor-2\)
C \(2N-2\)
D \(2N-4\)
答案:A
这题我认为是下取整啊。。。请大佬指教
10、下面的故事与()算法有异曲同工之妙。
从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事:“从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事:‘从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事……’”
A 枚举
B 递归
C 贪心
D 分治
答案:B
这不用我说,这耳熟能详的故事就是一种递归,自己套着自己,对递归的概念了解的话应该不难
11、由四个没有区别的点构成的简单无向连通图的个数是()。
A 6
B 7
C 8
D 9
答案:A
简单图:
在无向图中,关联一对顶点的无向边如果多于1条,则称这些边为平行边,平行边的条数称为重数。在有向图中,关联一对顶点的有向边如果多于1条,并且这些边的始点与终点相同(也就是它们的的方向相同),称这些边为平行边。含平行边的图称为多重图,既不含平行边也不含环的图称为简单图
自己画画即可 不要像我一样画多了
12、设含有10个元素的集合的全部子集数为S,其中有7个元素组成的子集数为T,则T/S的值为()。
A 5/32
B 15/128
C 1/8
D 21/128
答案:B
排列组合的题目
\(T=C^7_{10}=C^3_{10}=\frac{10*9*8}{3*2*1}=120\)
\(S=C^0_{10}+C^1_{10}+C^2_{10}+...+C^{10}_{10}=1024\)
于是
\(T/S=120/1024=15/128\)
13、10000以内,与10000互质的正整数有()个。
A 2000
B 4000
C 6000
D 8000
答案:B
容斥原理
\(10000\)的因数只有\(2\)和\(5\)
于是我们只要考虑\(10000\)以内有多少个\(2\)或\(5\)的倍数,再用\(10000\)减去即可
设\(10000\)以内\(2\)的倍数集合为\(A\),\(5\)的倍数集合为\(B\)
则有
\(|A\bigcup B|=|A|+|B|-|A\bigcap B|\)
于是
\(10000-|A\bigcup B|=[\frac{10000}{2}]+[\frac{10000}{5}]-[\frac{10000}{10}]=10000-6000=4000\)
14、为了统计一个非负整数的二进制形式中1的个数,代码如下:
int CountBit(int x){
int ret = 0;
while(x){
ret++;
__________;
}
return ret;
}
则空格内要填入的语句是:()
A x>>=1
B x&=x-1
C x|=x>>1
D x<<=1
答案:B
每执行一次x = x&(x-1),会将x用二进制表示时最右边的一个1变为0,因为x-1将会将该位(x用二进制表示时最右边的一个1)变为0。
这样每次消掉一个1,就可以得到1的个数了
千万不能选A!那是有多少个二进制位!
15、下图中所使用的数据结构是:()。
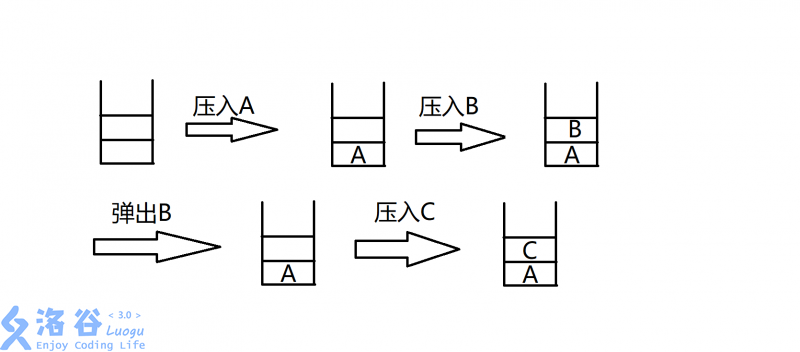
A 哈希表
B 栈
C 队列
D 二叉树
答案:B
栈的基本定义: LIFO(后进先出)
二、问题求解
1、甲乙丙丁四人在考虑周末要不要外出郊游。
已知①如果周末下雨,并且乙不去,则甲一定不去
②如果乙去,则丁一定去
③如果丙去,则丁一定不去
④如果丁不去,而且甲不去,则丙一定不去
如果周末丙去了,则甲___(去了/没去),
乙___(去了/没去),
丁___(去了/没去),
周末___(下雨/没下雨)。
答案:去了、没去、没去、没下雨
还算是比较简单的逻辑推理吧
③是突破口,之后慢慢推
2、从1到2018这2018个数中,共有____个包含数字8的数。
答案:544
小学奥数啊!初中的我快忘光了
数码问题,我用了一种类似于容斥原理的方法
计算含1个、2个、3个8的数的个数,然后容斥
三、阅读程序
1、
#include<cstdio>
char st[100];
int main(){
scanf("%s",st);
for(int i=0;st[i];++i){
if('A'<=st[i]&&st[i]<='Z')
st[i]+=1;
}
printf("%s\n",st);
return 0;
}
输入:QuanGuoLianSai
输出:_________
答案:RuanHuoMianTai
大写字母往后推一个,其他字母不变,很容易理解
2、
#include<cstdio>
int main(){
int x;
scanf("%d",&x);
int res=0;
for(int i=0;i<x;++i){
if(i * i % x == 1){
++res;
}
}
printf("%d",res);
return 0;
}
输入:15
输出:______
答案:4
求\(15^2\)以内的完全平方数有多少个模\(15\)余\(1\)
3、
#include<iostream>
using namespace std;
int n,m;
int findans(int n,int m){
if(n==0) return m;
if(m==0) return n%3;
return findans(n-1,m)-findans(n,m-1)+findans(n-1,m-1);
}
int main(){
cin>>n>>m;
cout<<findans(n,m)<<endl;
return 0;
}
输入:5 6
输出:____
答案:8
考场上完全看不懂他在干嘛,画了个巨大的解答树
这中间有不少重复计算的量,可以手动记忆化
我只发现了(5,6)=(2,6),这程序是在干什么望指教
4、
#include<cstdio>
int n,d[100];
bool v[100];
int main(){
scanf("%d",&n);
for(int i=0;i<n;++i){
scanf("%d",d+i);
v[i]=false;
}
int cnt=0;
for(int i=0;i<n;++i){
if(!v[i]){
for(int j=i;!v[j];j=d[j]){
v[j]=true;
}
++cnt;
}
}
printf("%d\n",cnt);
return 0;
}
输入:10 7 1 4 3 2 5 9 8 0 6
输出:_____
答案:6
按题意模拟即可
四、完善程序
1、(最大公约数之和) 下列程序想要求解整数n的所有约数两两之间最大公约数的和对10007求余后的值,试补全程序。
举例来说,4的所有约数是1,2,4。1和2的最大公约数为1,2和4的最大公约数为2,1和4的最大公约数为1,于是答案为1+2+1=4
要求getDivisor函数的复杂度为\(O(\sqrt{n})\),gcd函数的复杂度为\(O(log max(a,b))\)
#include<iostream>
using namespace std;
const int N=110000,P=10007;
int n;
int a[N],len;
int ans;
void getDivisor(){
int len=0;
for(int i=1;__(1)__;i++)
if(n%i==0){
a[++len]=i;
if(__(2)__!=i) a[++len]=n/i;
}
}
int gcd(int a,int b){
if(b==0){
__(3)__;
}
return gcd(b,__(4)__);
}
int main(){
cin>>n;
getDivisor();
ans=0;
for(int i=1;i<=len;i++){
for(int j=i+1;j<=len;j++){
ans=(__(5)__)%p;
}
}
cout<<ans<<endl;
return 0;
}
答案:i*i , n/i , return a, a%b , ans+gcd(a[i],a[j])
辗转相除法求最大公约数
求约数是注意完全平方数即可
2、
对于一个1到n的排列P(即1到n中每一个数在P中出现了恰好一次),令\(q_i\)为第i个位置之后第一个比\(P_i\)值更大的位置,则\(q_i=n+1\)。
举例来说,如果n=5且P为1 5 4 2 3,则q为2 6 6 5 6。
下列程序读入了排列P,使用双向链表求解了答案,试补全程序。
数据范围\(1\leq n \leq 10^5\)
#include<iostream>
using namespace std;
const int N = 100010;
int n;
int L[N],R[N],a[N];
int main(){
cin>>n;
for(int i=1;i<=n;++i){
int x;
cin>>x;
__(1)__;
}
for(int i=1;i<=n;++i){
R[i]=i+1;
L[i]=i-1;
}
for(int i=1;i<=n;++i){
L[__(3)__]=L[a[i]];
R[L[a[i]]]=R[__(4)__];
}
for(int i=1;i<=n;++i){
cout<<__(5)__<<" ";
}
cout<<endl;
return 0;
}
答案:a[x]=i , i+1 , R[a[i]] , a[i] , R[i]
考试时第一眼看着很懵
但一看他这么输入,估计得离散化!
剩下的就是双链表的基本操作了
祝大家胜利过初赛!