[Algorithm][Greedy] Prim’s Minimum Spanning Tree (MST)

概述

Prim算法也是一种贪婪算法，它从一个空的生成树开始，主要思想为维护两个集合：

　　1.S₁ ：一个集合包含已经存在于MST（Minimum Spanning Tree）中的节点

　　2.S₂ ：一个集合包含没有在MST中的节点

在每一步，它考虑任意一个能够链接两个集合的边，并且从中选择权重最小的边，然后将边的另一个端点加入到S₁中。

在图论中，连接两个集合的边被称为割 (cut)

生成树（spanning tree）：所有的节点都被连接

算法

1. 创建一个MstSet来维护已经在最小生成树里的点。

2. 给图中所有的点一个初始值，第一个点初始值为0，剩余的点初始值为无穷大，以便于我们从中选择第一个点。

3. （while）只要mstSet还没包含所有的点

　　a. 从不在mst的点中选择一个有最小值的点u

　　b. 把u放到mstSet里

　　c. 更新u的邻接点的值：遍历所有的值，对每一个邻接顶点，如果边u-v的权重比v之前的值要小，更新v的值为u-v的权重

例子

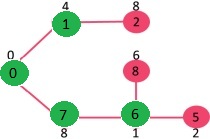
以上图为输入图

mstSet初始为空：{ } 所有顶点的值为{0, INF, INF, INF, INF, INF, INF, INF, INF}

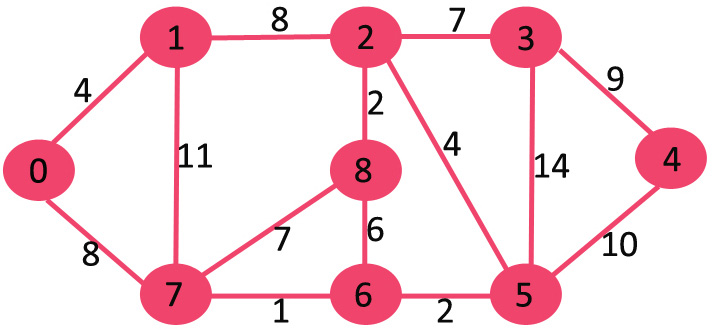
首先我们选择0点作为根节点, 将0放入mstSet并且更新邻接点的值

此时mstSet: { 0 } key: {4, 8, INF, INF, INF, INF, INF, INF}

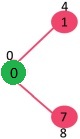
此时4为最小值，取出1放入mstSet并且更新key

mstSet: {0, 1} key: {8, 8, INF, INF, INF, INF, INF}

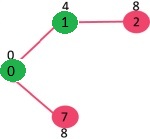
此时取出7：

mstSet: {0, 1, 7} key: {1, 7, 8, INF, INF, INF}

取出6:

mstSet: {0, 1, 7, 6} key: {2, 6, 8, INF, INF}

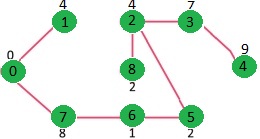
最后得到的树为：

实现

// A C / C++ program for Prim's Minimum Spanning Tree (MST) algorithm. 
// The program is for adjacency matrix representation of the graph
 
#include <stdio.h>
#include <limits.h>
 
// Number of vertices in the graph
#define V 5
 
// A utility function to find the vertex with minimum key value, from
// the set of vertices not yet included in MST
int minKey(int key[], bool mstSet[])
{
   // Initialize min value
   int min = INT_MAX, min_index;
 
   for (int v = 0; v < V; v++)
     if (mstSet[v] == false && key[v] < min)
         min = key[v], min_index = v;
 
   return min_index;
}
 
// A utility function to print the constructed MST stored in parent[]
int printMST(int parent[], int n, int graph[V][V])
{
   printf("Edge   Weight
");
   for (int i = 1; i < V; i++)
      printf("%d - %d    %d 
", parent[i], i, graph[i][parent[i]]);
}
 
// Function to construct and print MST for a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
     int parent[V]; // Array to store constructed MST
     int key[V];   // Key values used to pick minimum weight edge in cut
     bool mstSet[V];  // To represent set of vertices not yet included in MST
 
     // Initialize all keys as INFINITE
     for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;
 
     // Always include first 1st vertex in MST.
     key[0] = 0;     // Make key 0 so that this vertex is picked as first vertex
     parent[0] = -1; // First node is always root of MST 
 
     // The MST will have V vertices
     for (int count = 0; count < V-1; count++)
     {
        // Pick the minimum key vertex from the set of vertices
        // not yet included in MST
        int u = minKey(key, mstSet);
 
        // Add the picked vertex to the MST Set
        mstSet[u] = true;
 
        // Update key value and parent index of the adjacent vertices of
        // the picked vertex. Consider only those vertices which are not yet
        // included in MST
        for (int v = 0; v < V; v++)
 
           // graph[u][v] is non zero only for adjacent vertices of m
           // mstSet[v] is false for vertices not yet included in MST
           // Update the key only if graph[u][v] is smaller than key[v]
          if (graph[u][v] && mstSet[v] == false && graph[u][v] <  key[v])
             parent[v]  = u, key[v] = graph[u][v];
     }
 
     // print the constructed MST
     printMST(parent, V, graph);
}
 
 
// driver program to test above function
int main()
{
   /* Let us create the following graph
          2    3
      (0)--(1)--(2)
       |   /    |
      6| 8/   5 |7
       | /      |
      (3)-------(4)
            9          */
   int graph[V][V] = {{0, 2, 0, 6, 0},
                      {2, 0, 3, 8, 5},
                      {0, 3, 0, 0, 7},
                      {6, 8, 0, 0, 9},
                      {0, 5, 7, 9, 0},
                     };
 
    // Print the solution
    primMST(graph);
 
    return 0;
}

与Dijsktra的不同

dijsktra中使用从起点到该点的最小距离更新并以此做比较

Prim中使用这条边的权重来更新点的值，并以此做比较

参考链接：https://ide.geeksforgeeks.org/index.php